Aujourd’hui, nous allons travailler ensemble sur une notion fondamentale : l’algèbre linéaire ! Tu vas retrouver cette notion dans de nombreux concepts mathématiques, il est donc primordial de la comprendre et de savoir l’utiliser. Cet article est justement là pour te permettre de maîtriser toutes les propriétés et astuces sur l’algèbre linéaire. Tu pourras même t’entraîner avec deux exercices corrigés à la fin de cet article !
Qu’est-ce que l’algèbre linéaire ?
L’algèbre linéaire est une partie primordiale des mathématiques, qui utilise aussi bien les vecteurs (autrement dit la géométrie) que les fonctions linéaires (une partie plus algébrique). En effet, l’algèbre linéaire va nous permettre d’étudier les caractéristiques des vecteurs, de comprendre des fonctions linéaires et de résoudre des systèmes d’équations linéaires avec plusieurs variables.
Les vecteurs : le cœur de l’algèbre linéaire
Un vecteur se caractérise par trois éléments essentiels:
- Sa direction : correspondant à l’orientation de la droite sur laquelle se situe le vecteur
- Son sens : correspondant à la direction du vecteur indiquée par la flèche du vecteur
- Sa longueur : correspondant à la taille ou distance du segment du vecteur, aussi connue sous le nom de « norme » du vecteur
Pour représenter un vecteur, on prend deux points d’un plan tel que \( A \) et \( B \). Le vecteur \( \vec{u} = \vec{AB} \) correspond alors au mouvement qui déplace le point \( A \) vers le point \( B \). On parle de la translation du point \( A \) au point \( B \).
On a donc graphiquement :
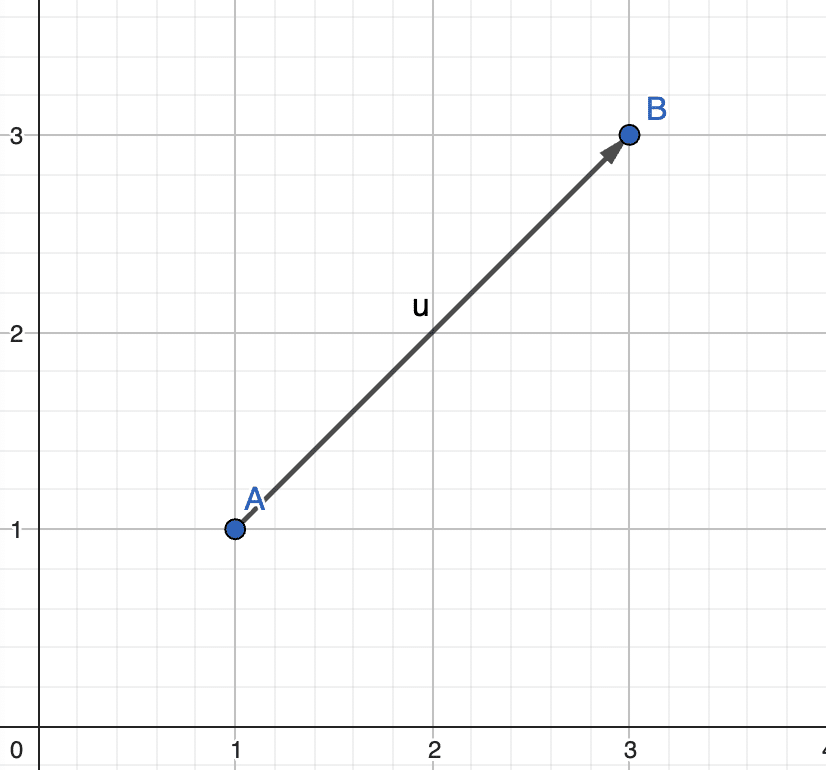
Graphique généré avec GeoGebra
Les opérations sur les vecteurs en algèbre linéaire
On peut réaliser une multitude d’opérations sur les vecteurs. Dans la majorité des cas, les opérations suivent une logique classique, puisqu’on réalise en réalité les opérations sur les coordonnées des vecteurs.
Ainsi, si on additionne ou soustrait des vecteurs, on additionne ou soustrait leurs coordonnées mutuellement. Par exemple, avec l’addition de deux vecteurs \( \vec{u}(x ; y) \)et \( \vec{v}(x’ ; y’) \), obtient :
\[ \displaystyle
\vec{u} + \vec{v} = (x + x’ \ ;\ y + y’)
\]
De même, pour la multiplication par un nombre réel \( k \), on obtient :
\[ \displaystyle
k \cdot \vec{u} = (k \cdot x \ ;\ k \cdot y)\]
La seule opération qui diffère est le produit scalaire. Le produit scalaire de deux vecteurs \( \vec{u}(x ; y) \)et \( \vec{v}(x’ ; y’) \) donne:
\[
\vec{u} \cdot \vec{v} = x \cdot x’ + y \cdot y’
\]
⚠️ Attention à ne pas faire d’erreur de rédaction dans tes calculs, surtout dans les matières scientifiques ! ⚠️
Les applications linéaires
Une application linéaire entre deux espaces vectoriels \( E \) et \( F \) est une fonction \( f : E \rightarrow F \) qui va permettre de passer d’un espace vectoriel à un autre. On dit qu’une application linéaire est stable par l’addition et la multiplication. Autrement dit, une fonction est une application linéaire si elle respecte :
- \( f(\vec{u} + \vec{v}) = f(\vec{u}) + f(\vec{v}) \)
- \( f(\lambda \vec{u}) = \lambda f(\vec{u}) \)
On a donc bien la définition d’une application linéaire donnée par \( \displaystyle \forall \lambda \in \mathbb{R} \) :
\[ \displaystyle
\forall (x, y) \in E^2,\quad f(\lambda x + y) = \lambda f(x) + f(y)
\]
Un exemple d’application linéaire est par exemple l’application \( \displaystyle f : \mathbb{R}^2 \rightarrow \mathbb{R}^2 \) définie par :
\[
f(x ; y) = (2x + y \ ;\ x – y)
\]
Les systèmes d’équations linéaires
Un système d’équations linéaires est défini comme un ensemble d’équations à plusieurs inconnues. Dans un système d’équation linéaire, on va donc retrouver plusieurs équations souvent du premier degré avec une ou plusieurs inconnues. Ce système va nous permettre de combiner les équations pour trouver les valeurs des inconnues. On va ainsi additionner, soustraire ou encore multiplier les différentes équations pour trouver les solutions du système.
Prenons un exemple pour mieux comprendre avec le système à deux équations et deux inconnues suivant :
\[ \displaystyle
\left\{
\begin{array}{l}
x + y = 3 \quad \text{(1)} \
2x – y = 1 \quad \text{(2)}
\end{array}
\right.
\]
Pour le résoudre on peut additionner les deux équations pour faire « disparaître » l’inconnu \( y \), on a alors :
\[
(x + y) + (2x – y) = 3 + 1
\]
\[
3x = 4
\]
\[ \displaystyle
x = \frac{4}{3}
\]
On obtient donc avec le système initial :
\[ \displaystyle
\frac{4}{3} + y = 3 \; \Leftrightarrow \; y = \frac{5}{3}
\]
Tu peux retenir que si un système comporte moins d’équations qu’il n’a d’inconnues, alors l’une des inconnues admettra une infinité de solutions. Autrement dit, le système admettra une infinité de solutions.
👉🏻 Tu as besoin d’un petit coup de pouce en mathématiques sur les racines carrées ou sur la fonction valeur absolue ? Jette un coup d’œil à nos articles sur tout ce qu’il faut savoir sur les racines carrées ou sur tout ce qu’il faut connaître sur la suite de Fibonacci et le nombre d’or 👈🏻
Exercices d’entraînement sur l’algèbre linéaire
Exercice 1
Soient trois points A, B, C : \( A(1\,;2) \), \( B(3\,;5) \) et \( C(-1\,;4) \).
- Détermine les coordonnées des vecteurs \( \displaystyle \vec{AB} \) et \( \vec{AC} \)
- Calcule \( \displaystyle \vec{AB} + \vec{AC} \)
- Calcule \( \displaystyle 2 \cdot \vec{AB} \)
Exercice 2
Résous le système d’équation linéaire suivant (à deux inconnues) :
\[ \displaystyle
\begin{cases}
x + y = 3 \\
2x – y = 1
\end{cases}
\]
Corrigés des exercices
Corrigé de l’exercice 1
Comme tu l’as compris, pour trouver les coordonnées d’un vecteur, tu dois utiliser les coordonnées des différents points de ce vecteur. On a donc d’après la formule du cours, les coordonnées suivantes :
\[ \displaystyle
\vec{AB} = (x_B – x_A\,;\; y_B – y_A) = (3 – 1\,;\; 5 – 2) = (2\,;\; 3)
\]
\[ \displaystyle
\vec{AC} = (x_C – x_A\,;\; y_C – y_A) = (-1 – 1\,;\; 4 – 2) = (-2\,;\; 2)
\]
Pour la somme, il suffit d’additionner les coordonées. On obtient :
\[ \displaystyle
\vec{AB} + \vec{AC} = (2\,;\; 3) + (-2\,;\; 2) = (2 + (-2)\,;\; 3 + 2) = (0\,;\; 5)
\]
Pour le produit, on a :
\[ \displaystyle
2 \cdot \vec{AB} = 2 \cdot (2\,;\; 3) = (2 \cdot 2\,;\; 2 \cdot 3) = (4\,;\; 6)
\]
Corrigé de l’exercice 2
Pour résoudre ce système, on va utiliser la méthode de la combinaison linéaire. On additionne la première ligne avec la seconde pour supprimer \( y \) et on a :
\[ \displaystyle
\begin{cases}
(x + y) + (2x – y) = 3 \\
2x – y = 1
\end{cases}
\]
\[ \displaystyle
\begin{cases}
3x = 4 \\
2x – y = 1
\end{cases}
\]
\[ \displaystyle
\begin{cases}
x = \frac{4}{3} \\
2x – y = 1
\end{cases}
\]
On remplace alors dans la deuxième ligne par le \( x \) obtenu et on a :
\[ \displaystyle
\begin{cases}
x = \frac{4}{3} \\
2 \times \frac{4}{3} – y = 1
\end{cases}
\]
\[ \displaystyle
\begin{cases}
x = \frac{4}{3} \\
y = \frac{5}{3}
\end{cases}
\]
Donc les solutions de ce système sont \( \displaystyle S = \frac{4}{3} \; ; \; \frac{5}{3} \).
Ce que tu dois retenir de l’algèbre linéaire
Voilà, tu connais maintenant tout en algèbre linéaire ! Tu es désormais capable d’expliquer ce qu’est un vecteur, une matrice ou encore de résoudre un système d’équations linéaires. Tu t’es même entraîné avec deux exercices sur cette notion fondamentale ! J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et lire cet article sur les techniques de conversion des unités de longueur !