Dans cet article, découvre comment étudier le comportement asymptotique en analyse.
En fait, une asymptote est une droite dont une courbe s’approche de plus en plus, sans jamais l’atteindre.
Illustration et exemple :
Définition
Soit \(D\) la droite d’équation \(y=ax+b\), et \(C_f\) la courbe d’équation \(y=f(x)\),
On dit que la droite \(D\) est asymptote à une courbe \(C_f\) en \(±\infty\) si la distance |\(f(x)-(ax+b)\)| entre la courbe \(C_f\) et la droite \(D\) tend vers \(0\) quand \(x\) tend vers \(±\infty\).
Trois cas particuliers
- Asymptote oblique :
Dire que la droite d’équation \(y=ax+b\) est asymptote à \(C_f\) en \(±\infty\) signifie qu’il est possible d’écrire \(f(x)=ax+b+g(x)\), où \(g\) est une fonction qui tend vers \(0\) quand \(x\) tend vers \(±\infty\).
- Asymptote horizontale :
Si \(a=0\), l’asymptote est parallèle à l’axe des abscisses.
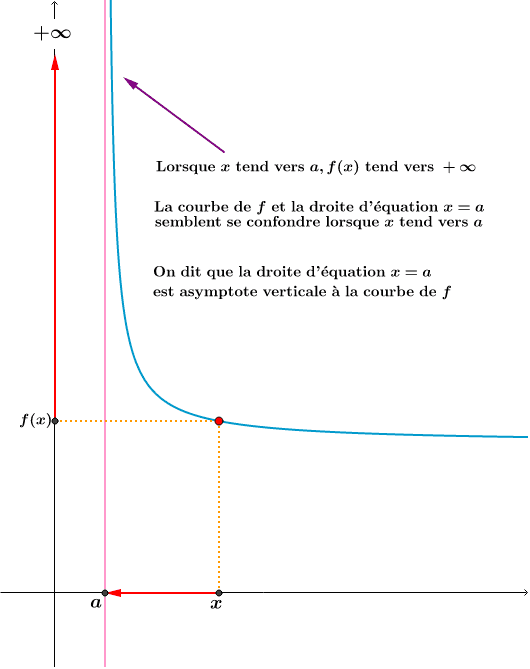
- Asymptote verticale :
On dit que la droite d’équation \(x=x_0\) est asymptote à \(C_f\) si, et seulement si,
-
- \(\lim \limits_{x \to x_0}f(x)=±\infty\),
- Ou si \(\lim \limits_{x \to x_0^+}f(x)=±\infty\),
- Ou encore si \(\lim \limits_{x \to x_0^-}f(x)=±\infty\)
L’asymptote est alors parallèle à l’axe des ordonnées.
Asymptotes en \(-\infty\), en \(+\infty\) et en \(x_0\)
Quand \(x\) tend vers \(±\infty\), on distingue trois cas :
- Si la limite de \(f\) est infinie, il est possible que \(C_f\) ait une asymptote oblique
\(\:\)
Attention : ce n’est pas certain.
On pourra utiliser comme contre-exemple la fonction \(f(x)=x^2\).
\(\:\) - Si la limite est finie (i.e. si \(l\) est la limite, où \(l \in \mathbb{R}\)), \(C_f\) a une asymptote horizontale dont l’équation est \(y=l\).
\(\:\) - Si la limite n’existe pas, \(C_f\) n’a pas d’asymptote.
\(\:\)
Exemple : Si \(f(x)=x sin(x)\), \(C_f\) n’a pas d’asymptote car \(f(x)\) change constamment de signe quand \(x\) tend vers \(±\infty\).
Quand \(x\) tend vers une “valeur interdite” \(x_0\), la courbe peut avoir une asymptote verticale d’équation \(x=x_0\), mais ce n’est pas toujours le cas.
Exemple : Pour \(f(x)=x ln(x)\), \(C_f\) n’a pas d’asymptote en \(0\) car \(\lim \limits_{x \to x_0^+}f(x)=0\).