Dans cet article, nous allons travailler ensemble sur une notion fondamentale en mathématiques : la fonction inverse ! Tu vas retrouver cette notion dans de nombreux concepts et théorèmes mathématiques, il est donc primordial de la comprendre et de savoir l’utiliser. Cet article est justement là pour te permettre de maîtriser toutes les propriétés et astuces sur la fonction inverse. Tu pourras même t’entraîner avec deux exercices corrigés en fin de cet article !
Qu’est-ce que la fonction inverse ?
La fonction inverse associe à chaque nombre \( \displaystyle x \in \mathbb{R}^* \) (l’ensemble des réels non nuls) son inverse \( \displaystyle \frac{1}{x} \). On peut aussi dire que la fonction inverse renvoie ce nombre à sa puissance \( – 1 \). Cette fonction est donc définie sur \( \displaystyle \mathbb{R}^* \). Ainsi, la fonction inverse est définie par :
\[ \displaystyle f(x) = \frac{1}{x}, \quad \text{pour } x \neq 0. \]
Prenons quelques exemples pour mieux comprendre comment fonctionne cette fonction. Si je cherche l’inverse de \( 8 \), alors ce sera \( \displaystyle \frac{1}{8} \). Mais de la même manière (et tu l’utiliseras souvent dans tes exercices, y compris à l’épreuve de spécialité de mathématiques), si je cherche l’inverse d’un huitième, autrement de \( \displaystyle \frac{1}{8} \), alors ce sera \( \displaystyle \frac{1}{\frac{1}{8}} = 8 \). L’inverse de l’inverse d’un nombre est donc le nombre lui-même !
Voici d’autres exemples :
- \( f(1) = 1 \)
- \( \displaystyle f(2) = \frac{1}{2} = 0.5 \)
- \( \displaystyle f(4) = \frac{1}{4} = 0.25 \)
- \( \displaystyle f(0.5) = \frac{1}{0.5} = 2 \)
- \( \displaystyle f(-1) = \frac{1}{-1} = -1 \)
- \( \displaystyle f(-3) = \frac{1}{-3} = -\frac{1}{3} \)
Propriétés de la fonction inverse
Décroissance de la fonction inverse
La fonction inverse est décroissante sur \( \displaystyle \mathbb{R}^* \). Autrement dit, plus \( x \) est grand, plus la valeur de \( f(x) \) sera petite. On peut facilement l’observer avec les trois premières valeurs de la fonction inverse. \[ \displaystyle f(1) = 1 > f(2)= \frac{1}{2} > f(3) = \frac{1}{3} \]
Les limites de la fonction inverse
La fonction inverse admet 4 limites différentes aux bornes de son ensemble de définition, autrement dit en \( \displaystyle -\infty, \ 0^{-}, \ 0^{+}, \ +\infty \). Les limites en \( -\infty \) et \( \ +\infty \) sont les mêmes car on fait tendre le dénominateur vers un nombre infini avec un numérateur constant égal à 1 donc nécessairement les limites vont tendre vers 0.
Au contraire, en \( \ 0^{-} \) et \( \ 0^{+} \) les limites seront « opposées » puisqu’on fait cette fois tendre le dénominateur vers \( \ 0^{-} \) et \( \ 0^{+} \) avec un numérateur constant égal à 1. Donc, les limites seront \( -\infty \) et \( \ +\infty \). On a donc :
- \( \displaystyle \lim\limits_{x \to 0^-} \frac{1}{x} = -\infty \)
- \( \displaystyle \lim\limits_{x \to 0^+} \frac{1}{x} = +\infty \)
- \( \displaystyle \lim\limits_{x \to -\infty} \frac{1}{x} = 0 \)
- \( \displaystyle \lim\limits_{x \to +\infty} \frac{1}{x} = 0 \)
⚠️ Attention à ne pas faire d’erreur de rédaction dans tes calculs, surtout dans les matières scientifiques !
Ses différentes asymptotes
Comme tu l’as compris au travers de ses limites, la fonction inverse admet donc deux asymptotes :
- une asymptote horizontale \( y = 0 \) en l’infini
- une asymptote verticale \( x = 0 \) en 0.
Représentation graphique de la fonction inverse
Voici la courbe représentative de la fonction inverse. C’est une hyperbole ! De plus, on voit que cette fonction est strictement décroissante sur \( \displaystyle \mathbb{R}^* \). On visualise aussi bien les 4 limites et les 2 asymptotes de la fonction inverse ici 😉
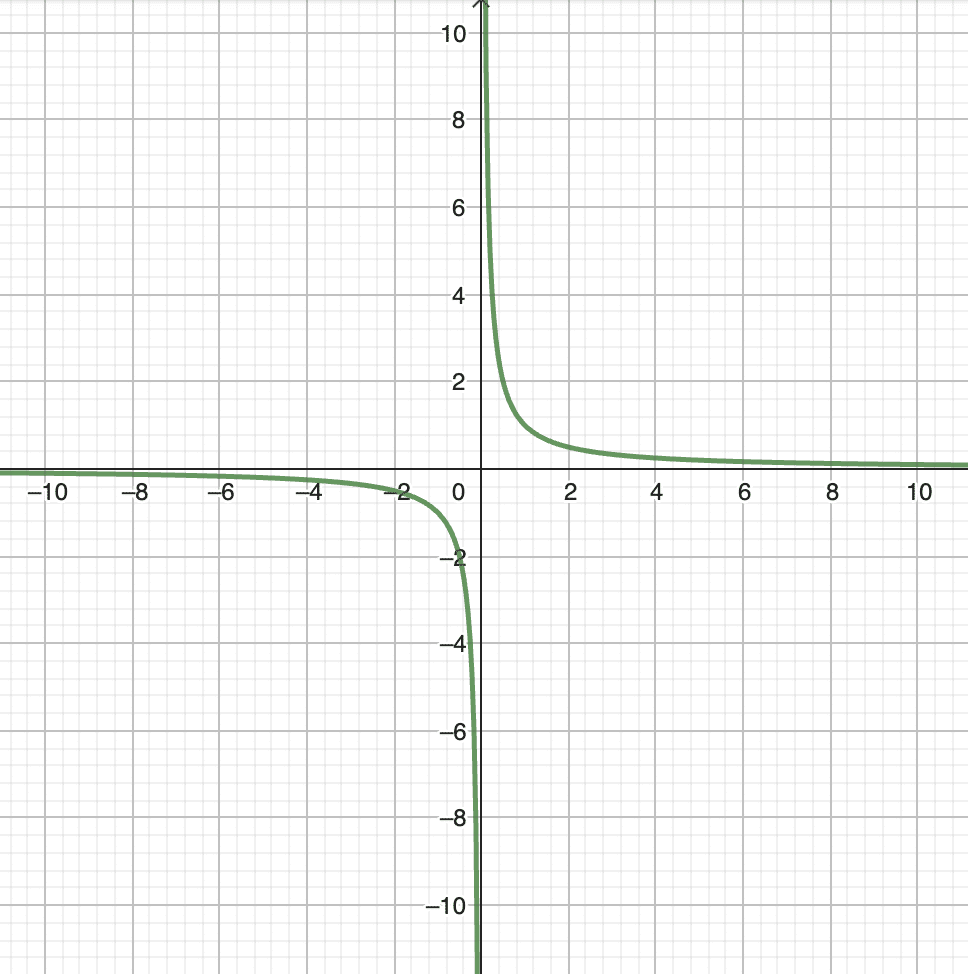
Graphique généré avec GeoGebra
Parité
La fonction inverse est impaire. On peut le voir facilement avec sa représentation graphique, puisque sa courbe est symétrique par rapport à l’origine du repère. Mais plus largement, cette fonction est impaire car :
\[ \displaystyle f(-x) = – \frac{1}{x} = -f(x) \]
Dérivée de la fonction inverse
La fonction inverse est dérivable sur son ensemble de définition, autrement dit sur \( \displaystyle \mathbb{R}^* \) et sa dérivée te sera très utile en mathématiques ! Sa dérivée est donnée par :
\[ \displaystyle \forall x \in \mathbb{R}^* \quad f'(x) = -\frac{1}{x^2} \]
Opérations avec la fonction inverse
Additions et les soustractions
Les additions et les soustractions avec la fonction inverse sont plus difficiles que la multiplication et la division. Il faudra faire passer les valeurs des dénominateurs aux numérateurs et les additionner ou les soustraire. Dans les deux cas, il faudra aussi multiplier les deux dénominateurs dans ta fraction finale.
Mais tu peux retenir deux formules qui sont toujours valables pour les additions et les soustractions. Si on choisit f comme la fonction inverse, alors on a :
Pour l’addition, \( \displaystyle f(x) + f(y) = \frac{1}{x} + \frac{1}{y} = \frac{x + y}{xy} \)
Pour les soustractions, \( \displaystyle f(x) – f(y) = \frac{1}{x} – \frac{1}{y} = \frac{y – x }{xy}\)
Divisions et multiplications
Pour les divisions et les multiplications, les calculs sont plus simples ! Il suffit de multiplier chaque valeur linéairement (le premier numérateur est multiplié avec le second, de même pour les dénominateurs).
Ainsi, on obtient les deux formules suivantes pour les divisions et les multiplications avec la fonction inverse :
Pour la division, \( \displaystyle f(x) \times f(y) = \frac{1}{x} \times \frac{1}{y} = \frac{1}{xy} \)
Pour la multiplication, \( \displaystyle \frac{f(y)}{f(x)} = \frac{\frac{1}{x}}{\frac{1}{y}} = \frac{1}{x} \times \frac{y}{1} = \frac{x}{y} \)
Puissance avec la fonction inverse
Enfin, pour les puissances, le calcul est lui aussi très simple puisque la puissance s’applique au numérateur et au dénominateur. On a donc \( \left( \frac{1}{x} \right)^n = \frac{1}{x^n} \) !
Astuces sur la fonction inverse
Comparer des valeurs de la fonction inverse
Pour comparer des valeurs de la fonction inverse selon les valeurs de \( x \), tu peux retenir que si on choisit deux valeurs a et b, avec \( \displaystyle a > b \) alors on a \( \displaystyle \frac{1}{a} < \frac{1}{b} \).
Prenons un exemple. Si on choisit 6 et 4, on a \( 6 > 4 \). Or \( \displaystyle \frac{1}{6} \approx 0.1666 \) alors que \( \displaystyle \frac{1}{4} = 0.25 \). On retrouve bien \( \displaystyle \frac{1}{6} < \frac{1}{4} \).
La partie entière en python
Enfin, dans le langage python, tu peux écrire la fonction inverse comme les autres fonctions (racine carrée, fonction valeur absolue, …). Elle est relativement simple, car la fonction inverse ne nécessite pas de formule compliquée: il s’agit simplement de \( \displaystyle \frac{1}{x} \).
Mais, attention, la valeur \( x = 0 \) doit être exclue et tu dois aussi le mentionner dans ton code python. Tu peux utiliser un code avec un if et un else. Pour rappel, le langage python est un langage informatique de programmation. Tu peux d’ailleurs t’entraîner à écrire en python sur divers sites, tels que mycompilateur.
👉🏻 Tu as besoin d’un petit coup de pouce en mathématiques sur les racines carrées ou sur la fonction valeur absolue ? Jette un coup d’œil à nos articles sur tout ce qu’il faut savoir sur les racines carrées ou sur tout ce qu’il faut connaître sur la valeur absolue 👈🏻
Exercices d’entraînement
Exercice 1 : Calculs simples avec la fonction inverse
Soit f la fonction inverse définie sur \( \displaystyle \mathbb{R}^* \). Calcule les valeurs suivantes :
- \( f(2) \)
- \( f(0.25) \)
- \( f(2^2 \)
- \( f(-3) \)
- \( \displaystyle f(2) \times f(4) \)
- \( \displaystyle \frac{f(3)}{f(6)} \)
- \( \displaystyle f(2) \times f\left( \frac{1}{6} \right) \)
Exercice 2 : Récurrence mathématique
Soit une suite définie pour tout entier naturel \( n \geq 1 \) par :
\[ \displaystyle u_1 = 1, \quad u_{n+1} = \frac{1 + u_n}{1}, \quad \forall n \geq 1. \]
Démontre, par récurrence (en utilisant la fonction inverse), que :
\[ \displaystyle \forall n \geq 1, \quad u_{n+1} \leq u_n. \]
Correction des exercices
Corrigé Exercice 1
Voici les valeurs pour chaque valeur demandée avec les calculs pour obtenir ces valeurs :
- \( \displaystyle f(2) = \frac{1}{2} = 0.5 \)
- \( \displaystyle f(0.25) = \frac{1}{0.25} = 4 \)
- \( \displaystyle f(2^2) = f(4) = \frac{1}{4} = 0.25 \)
- \( \displaystyle f(-3) = \frac{1}{-3} = -\frac{1}{3} \approx -0.333 \)
Pour les multiplications et la division, on commence par calculer les valeurs de f.
On a \( f(2) = 0.5 \) et \( \displaystyle f(4) = \frac{1}{4} = 0.25 \), on trouve donc :
- \( \displaystyle f(2) \times f(4) = 0.5 \times 0.25 = 0.125 \)
De même, \( \displaystyle f(3) = \frac{1}{3} \) et \( \displaystyle f(6) = \frac{1}{6} \), d’où :
- \( \displaystyle \frac{f(3)}{f(6)} = \frac{1}{3} \times \frac{6}{1} = 2 \)
Enfin, on a \( f(2) = 0.5 \) et \( \displaystyle f\left( \frac{1}{6} \right) = 6 \), alors :
- \( \displaystyle f(2) \times f\left( \frac{1}{6} \right) = 0.5 \times 6 = 3 \)
Corrigé Exercice 2
On raisonne par récurrence. On commence donc par l’Initialisation, qui commence ici à \( 1 \).
Pour \( n = 1 \) on a:
\[ \displaystyle u_2 = \frac{1 + u_1}{1} = \frac{1 + 1}{1} = \frac{2}{1} = 2. \]
Or \( u_1 = 1 \). On a donc bien \( u_2 \leq u_1 \). Donc la propriété est vraie au premier rang, la propriété est donc initialisée.
On passe à l’hérédité ! Supposons que la propriété est vraie à partir d’un certain entier naturel \( n \), tel que :
\[ \displaystyle u_{n+1} \leq u_n \]
Montrons alors que cette propriété est encore vraie au rang \( n +1 \), tel que :
\[ \displaystyle u_{n+2} \leq u_{n+1} \]
Autrement dit, il faut montrer que \[ \displaystyle \frac{1 + u_n}{1} \geq \frac{1 + u_{n+1}}{1}. \]
Or on sait que la fonction \( f \) est très proche de la fonction inverse et que cette fonction est décroissante sur \( \mathbb{R}^* \). On aurait pu le prouver à nouveau en dérivant cette fonction. Comme \( f \) est décroissante et définie sur le même intervalle que la suite \( u_n \) on peut alors écrire que:
\[ \displaystyle f(u_n) \geq f(u_{n+1}) \sim \frac{1 + u_n}{1} \geq \frac{1 + u_{n+1}}{1} \]
D’où \( \displaystyle u_{n+2} \leq u_{n+1} \)
La propriété est héréditaire.
👉🏻 Conclusion : comme la proposition est initialisée et héréditaire, on a bien démontré par récurrence que cette propriété est vraie pour toutes valeurs de \( n \) supérieure ou égal à 1. Donc cette suite \( u_n \) est décroissante sur \( \displaystyle \mathbb{N}^* \).
Le mot de la fin !
Voilà, tu connais maintenant tout sur la fonction inverse ! Tu es désormais capable de donner sa définition ainsi que ses propriétés et tu peux effectuer différentes opérations avec la fonction inverse ! Tu t’es même entraîné avec deux exercices. J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et lire cet article sur les techniques de conversion des unités de longueur !