Prêt à explorer un concept super puissant qui relie l’algèbre et la géométrie ? Imagine un instant que tu es en train de tracer des courbes et que tu veux connaître exactement comment elles se comportent à un point précis. C’est ici que le nombre dérivé entre en jeu ! Il te donne la pente de la tangente à une courbe en un point précis, ce qui est hyper utile pour comprendre comment une fonction évolue. Mais ce n’est pas tout : cette tangente, c’est aussi une ligne droite qui effleure la courbe en un point, reliant ainsi algèbre et géométrie de manière magique. Dans cet article, on va te montrer comment calculer ce nombre dérivé et comprendre son lien avec la tangente. C’est parti !
Rappels et explications sur le nombre dérivé et la tangente
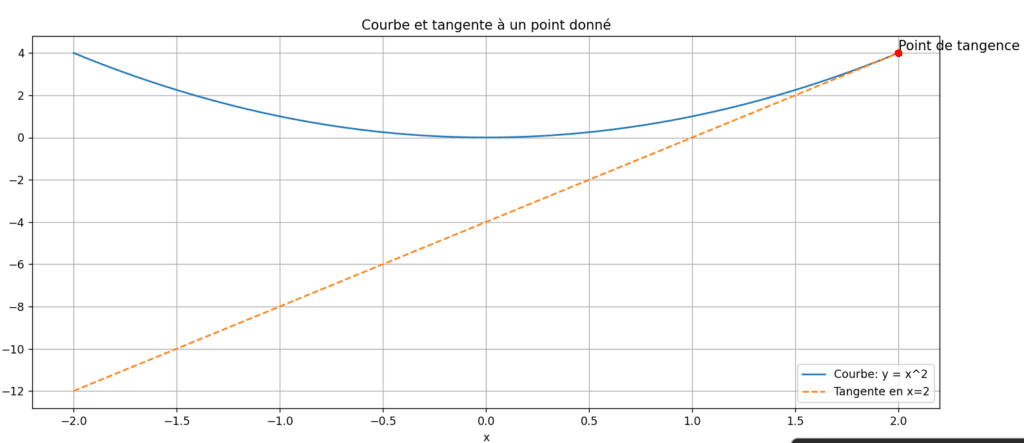
1. Rappel sur la tangente à une courbe
Une tangente à une courbe en un point donné est une droite qui touche la courbe en ce point sans la traverser. Imagine une parabole, comme \( y = x^2 \). La tangente en un point de cette parabole touche la courbe exactement en ce point et a la même direction que la courbe à cet endroit.
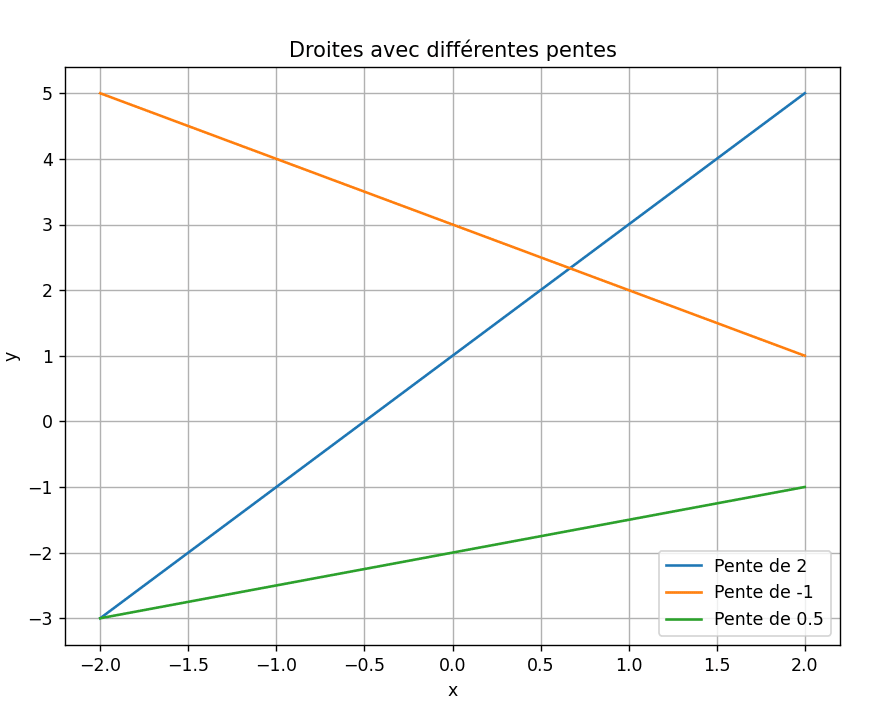
2. Coefficient directeur
Le coefficient directeur d’une droite est une mesure de la pente de cette droite. Pour une droite d’équation \( y = mx + b \), le coefficient directeur est \( m \). Par exemple, la droite \( y = 2x + 1 \) a un coefficient directeur de 2, ce qui signifie qu’elle monte de 2 unités pour chaque unité de déplacement horizontal.
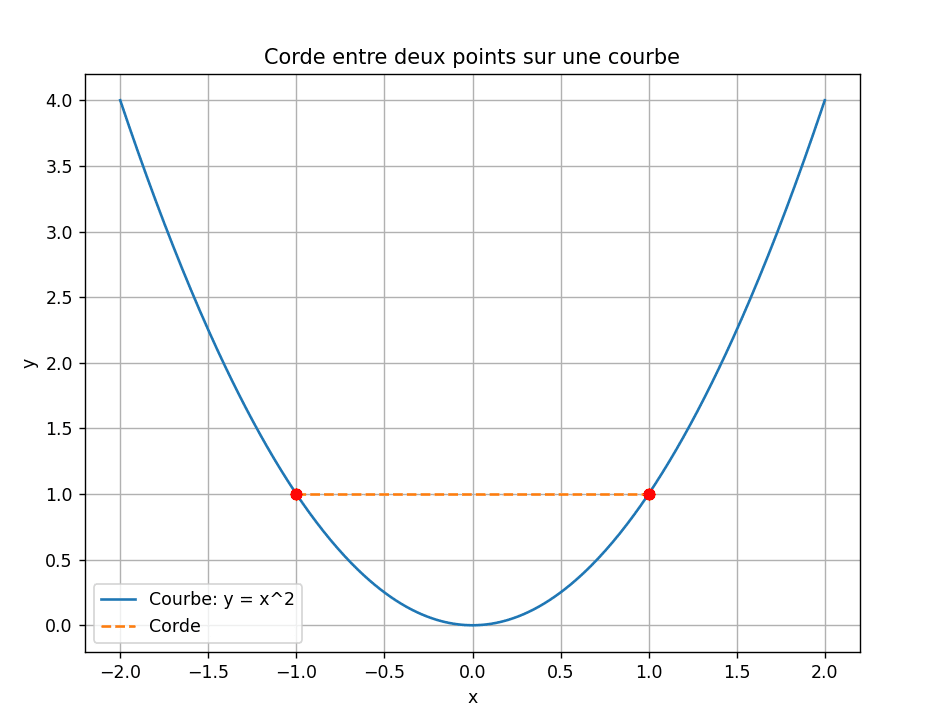
3. Taux d’accroissement d’une corde
Le taux d’accroissement d’une corde entre deux points \( (x_1, y_1) \) et \( (x_2, y_2) \) sur une courbe est donné par la formule :
\[ \text{Taux d’accroissement} = \frac{y_2 – y_1}{x_2 – x_1} \]
Ce taux représente la pente de la corde reliant ces deux points.
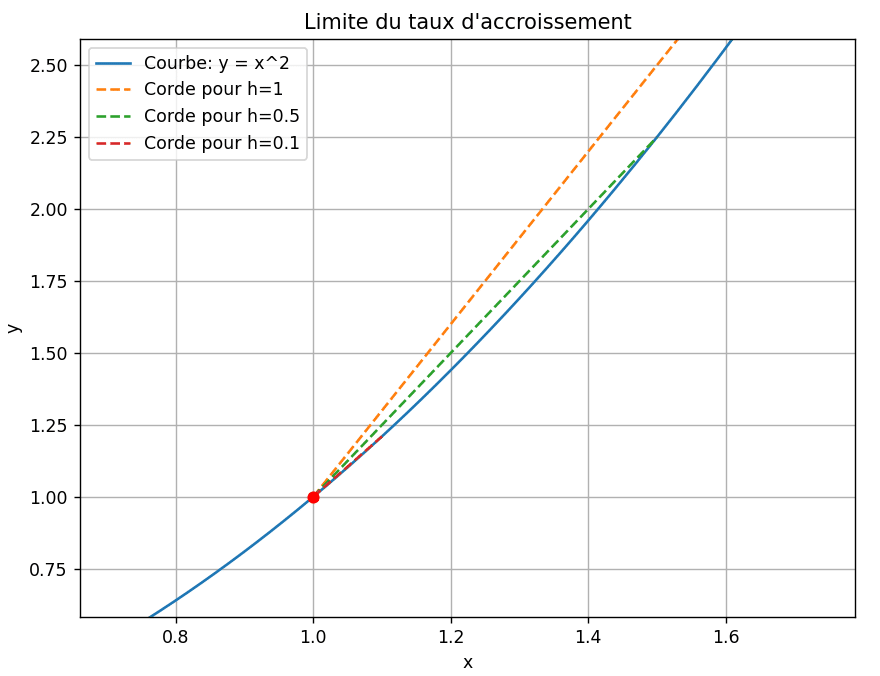
4. Nombre dérivé et limite du taux d’accroissement
Le nombre dérivé d’une fonction en un point est la limite du taux d’accroissement lorsque l’intervalle entre les deux points tend vers zéro. Mathématiquement, pour une fonction \( f \) et un point \( a \), le nombre dérivé est :
\[ f'(a) = \lim_{h \to 0} \frac{f(a+h) – f(a)}{h} \]
Ce nombre dérivé représente la pente de la tangente à la courbe au point \( a \).
5. Interprétation géométrique
Ainsi, le nombre dérivé, qui est une notion algébrique, peut être interprété géométriquement comme la pente de la tangente à la courbe en un point. Cela signifie que, en un point donné, la pente de la tangente à la courbe est égale au nombre dérivé de la fonction en ce point.
Méthodes à connaître
Détermination de la dérivée à partir d’un graphique
La détermination de la dérivée d’une fonction à partir de son graphique est une méthode graphique utilisée lorsque l’on cherche à comprendre comment la fonction évolue sans connaître son expression analytique.
Situation
Cette méthode intervient principalement lorsque tu as accès au graphique d’une fonction et que tu souhaites en déterminer la dérivée. Cela peut être utile lors de l’analyse de données expérimentales ou lorsque la fonction n’est pas connue analytiquement.
Démarche à suivre
Pour déterminer la dérivée d’une fonction à partir de son graphique, suis ces étapes :
1. **Identifie les points d’intérêt** : Choisis plusieurs points sur la courbe où tu souhaites estimer la dérivée.
2. **Trace les tangentes** : À chacun de ces points, trace la tangente à la courbe.
3. **Calcule les pentes des tangentes** : La pente de chaque tangente correspond à la valeur de la dérivée de la fonction en ce point. Utilise la formule de la pente entre deux points proches pour estimer cette pente.
Pourquoi cette méthode fonctionne-t-elle ?
Cette méthode fonctionne parce que, par définition, la dérivée d’une fonction en un point donné est la pente de la tangente à la courbe de la fonction en ce point. Ainsi, en calculant ces pentes pour plusieurs points, tu obtiens une estimation de la dérivée de la fonction.
Exemple d’application
Considérons la fonction \( f(x) = x^2 \). Voici comment on pourrait déterminer sa dérivée à partir de son graphique.
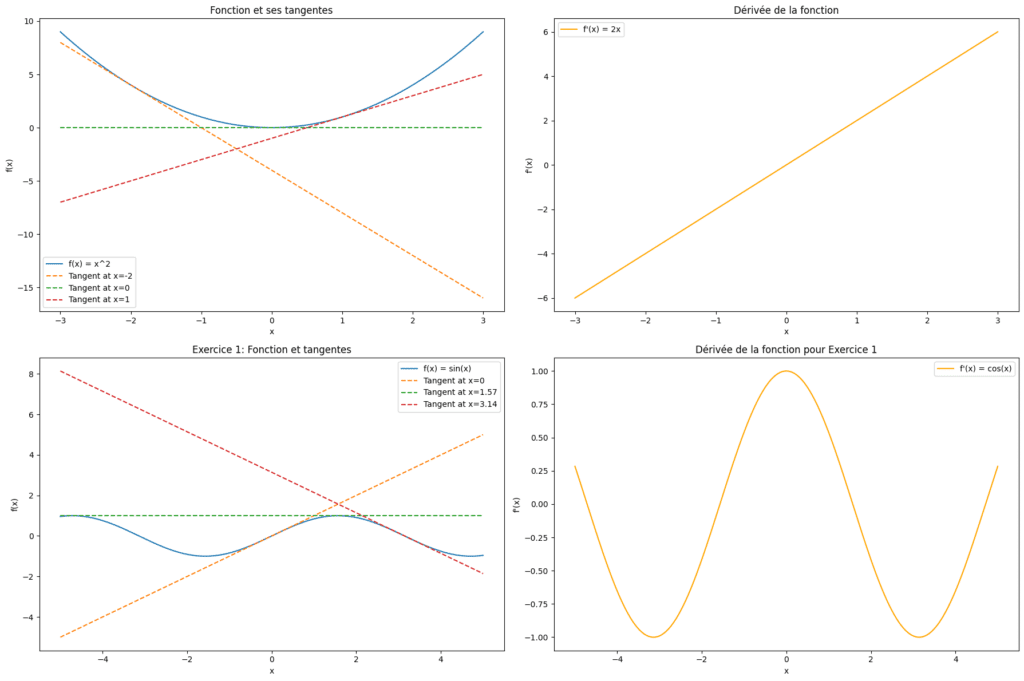
Pour différentes valeurs de \( x \), par exemple \( x = -2, 0, 1 \), on trace les tangentes à la courbe et on calcule leurs pentes. Par exemple, la pente de la tangente en \( x = 1 \) donne la valeur de la dérivée à ce point.
Essaye ces exercices pour t’entraîner à déterminer la dérivée à partir du graphique d’une fonction.
Exercices
Exercice 1
Soit la fonction \( f(x) = \sin(x) \). Utilise son graphique pour estimer les valeurs de la dérivée aux points \( x = 0, \frac{\pi}{2}, \pi \).
Voir la correction
Pour \( f(x) = \sin(x) \), la dérivée est \( f'(x) = \cos(x) \).
- En \( x = 0 \), la pente de la tangente est 1, correspondant à \( \cos(0) = 1 \).
- En \( x = \frac{\pi}{2} \), la pente est 0, correspondant à \( \cos(\frac{\pi}{2}) = 0 \).
- En \( x = \pi \), la pente est -1, correspondant à \( \cos(\pi) = -1 \).
Exercice 2
Considérons la fonction représentée graphiquement par une courbe parabolique. Estime la dérivée en \( x = 2 \) si la tangente à ce point passe par les points (2, 4) et (4, 8).
Voir la correction
La pente de la tangente, et donc la dérivée en \( x = 2 \), est calculée comme suit :
Pente = (change en y) / (change en x) = (8 – 4) / (4 – 2) = 2.
Donc, la dérivée à \( x = 2 \) est 2.
Calcul du nombre dérivé à partir de la définition
Le calcul du nombre dérivé à partir de sa définition est une compétence fondamentale en analyse mathématique, particulièrement utile lorsque tu commences à explorer les concepts de la dérivation.
Situation
Cette méthode intervient lorsque tu dois trouver la dérivée d’une fonction en un point spécifique sans utiliser les règles de dérivation. Elle est souvent employée dans les problèmes où la fonction n’est pas explicitement donnée ou pour renforcer la compréhension du concept de limite.
Démarche à suivre
Pour calculer le nombre dérivé d’une fonction \( f \) en un point \( a \) en utilisant la définition, suis ces étapes :
1. **Écrivez le taux d’accroissement** : Le taux d’accroissement de \( f \) entre \( a \) et \( a+h \) est donné par \( \frac{f(a+h) – f(a)}{h} \).
2. **Simplifie l’expression** : Simplifie l’expression du taux d’accroissement autant que possible.
3. **Calcule la limite lorsque \( h \) tend vers 0** : Le nombre dérivé est la limite de ce taux d’accroissement lorsque \( h \) tend vers 0.
Pourquoi cette méthode fonctionne-t-elle ?
Cette méthode fonctionne parce qu’elle est basée sur la définition même de la dérivée : la pente de la tangente à la courbe de la fonction en un point donné. En calculant la limite du taux d’accroissement, on trouve effectivement cette pente.
Exemple d’application
Considérons la fonction \( f(x) = x^2 \). Calculons son nombre dérivé en \( x = 1 \) en utilisant la définition.
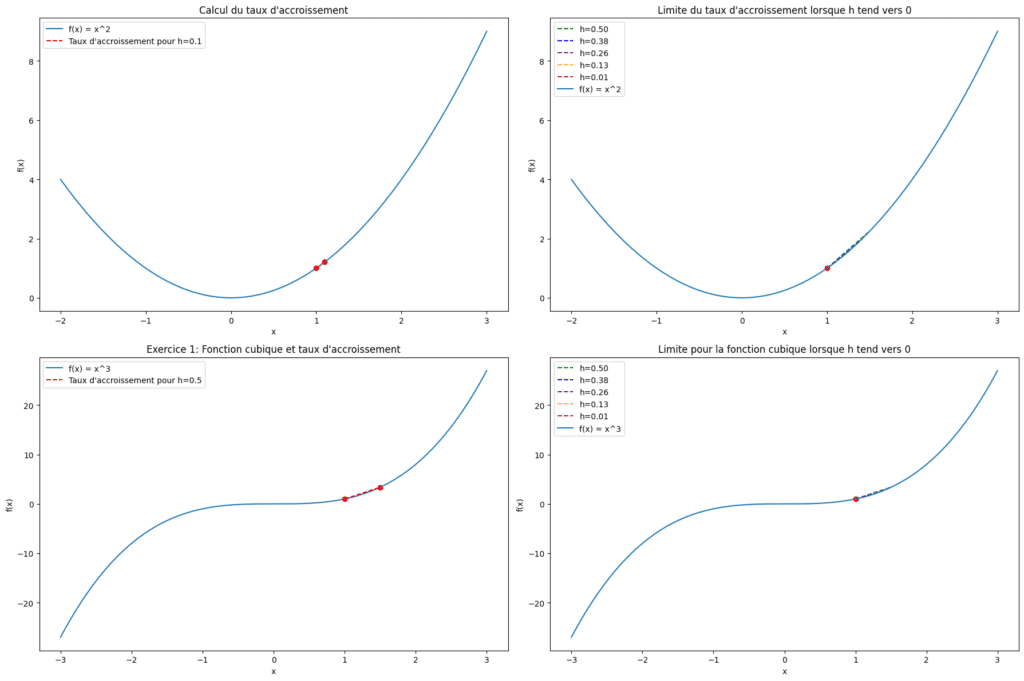
En utilisant la définition, on calcule :
\[ f'(1) = \lim_{h \to 0} \frac{(1+h)^2 – 1^2}{h} = \lim_{h \to 0} \frac{1 + 2h + h^2 – 1}{h} = \lim_{h \to 0} (2 + h) = 2 \]
Exercices
Essaye ces exercices pour t’entraîner à calculer le nombre dérivé à partir de la définition.
Exercice 1
Soit la fonction \( f(x) = x^3 \). Calcule le nombre dérivé de \( f \) en \( x = 1 \) en utilisant la définition de la dérivée.
Voir la correction
En utilisant la définition, nous calculons :
\[ f'(1) = \lim_{h \to 0} \frac{(1+h)^3 – 1^3}{h} = \lim_{h \to 0} \frac{1 + 3h + 3h^2 + h^3 – 1}{h} = \lim_{h \to 0} (3 + 3h + h^2) = 3 \]
Donc, le nombre dérivé de \( f(x) = x^3 \) en \( x = 1 \) est 3.
Exercice 2
Calcule le nombre dérivé de la fonction \( f(x) = \sqrt{x} \) en \( x = 4 \).
Voir la correction
En utilisant la définition, nous calculons :
\[ f'(4) = \lim_{h \to 0} \frac{\sqrt{4+h} – \sqrt{4}}{h} \]
Pour simplifier, multipliez le numérateur et le dénominateur par le conjugué du numérateur :
\[ \frac{\sqrt{4+h} – 2}{h} \cdot \frac{\sqrt{4+h} + 2}{\sqrt{4+h} + 2} = \frac{(4+h) – 4}{h (\sqrt{4+h} + 2)} = \frac{h}{h (\sqrt{4+h} + 2)} = \frac{1}{\sqrt{4+h} + 2} \]
En prenant la limite lorsque \( h \) tend vers 0, nous trouvons :
\[ f'(4) = \frac{1}{2 + 2} = \frac{1}{4} \]
Donc, le nombre dérivé de \( f(x) = \sqrt{x} \) en \( x = 4 \) est \( \frac{1}{4} \).
Équation de la tangente à une courbe en un point donné
Situation
On utilise cette méthode quand on veut connaître l’équation de la droite tangente à une courbe en un point spécifique. Ça peut être super pratique pour comprendre comment une fonction évolue autour de ce point.
Démarche à suivre
Voici comment tu peux trouver cette équation de la tangente :
1. **Trouve la dérivée de la fonction** : La dérivée te donne la pente de la tangente en tout point de la fonction.
2. **Calcule la pente en ton point d’intérêt** : Utilise la dérivée pour trouver la pente de la tangente au point donné.
3. **Utilise l’équation point-pente** : Avec la pente trouvée et les coordonnées du point, tu peux écrire l’équation de la tangente sous la forme \( y = mx + b \).
Pourquoi cette méthode fonctionne
Cette méthode est cool parce que la tangente est une ligne droite qui touche la courbe à un seul point et a la même pente que la courbe en ce point. Donc, en utilisant la dérivée, qui te donne cette pente, tu peux déterminer l’équation exacte de cette droite.
Exemple d’application
Considérons la fonction \( f(x) = x^2 \). Trouvons l’équation de la tangente en \( x = 1 \).
1. La dérivée de \( f(x) = x^2 \) est \( f'(x) = 2x \).
2. La pente en \( x = 1 \) est \( f'(1) = 2 \times 1 = 2 \).
3. La tangente passe par le point (1, 1), donc son équation est : \( y – 1 = 2(x – 1) \), ce qui simplifie à \( y = 2x – 1 \).
Exercices
À toi de jouer ! Voici quelques exercices pour t’entraîner à trouver l’équation de la tangente.
Exercice 1
Trouve l’équation de la tangente à la courbe \( f(x) = x^3 \) au point où \( x = 1 \).
Voir la correction
1. La dérivée de \( f(x) = x^3 \) est \( f'(x) = 3x^2 \).
2. La pente en \( x = 1 \) est \( f'(1) = 3 \times 1^2 = 3 \).
3. La fonction passe par le point (1, 1), donc l’équation de la tangente est : \( y – 1 = 3(x – 1) \), ce qui donne \( y = 3x – 2 \).
Exercice 2
Trouve l’équation de la tangente à la courbe \( f(x) = e^x \) au point où \( x = 1 \).
Voir la correction
1. La dérivée de \( f(x) = e^x \) est \( f'(x) = e^x \).
2. La pente en \( x = 1 \) est \( f'(1) = e^1 = e \).
3. La fonction passe par le point (1, e), donc l’équation de la tangente est : \( y – e = e(x – 1) \), ce qui donne \( y = e x \).
Exercice 3
Trouve l’équation de la tangente à la courbe \( f(x) = \sin(x) \) au point où \( x = \frac{\pi}{2} \).
Voir la correction
1. La dérivée de \( f(x) = \sin(x) \) est \( f'(x) = \cos(x) \).
2. La pente en \( x = \frac{\pi}{2} \) est \( f'(\frac{\pi}{2}) = \cos(\frac{\pi}{2}) = 0 \).
3. La fonction passe par le point (π/2, 1), donc l’équation de la tangente est : \( y – 1 = 0(x – \frac{\pi}{2}) \), ce qui donne \( y = 1 \).
Détermination des points où la tangente a une pente donnée
Situation
Cette méthode est utilisée quand on veut savoir où exactement sur une courbe la tangente a une pente précise. C’est particulièrement utile pour analyser le comportement d’une fonction et pour des applications en physique ou en ingénierie.
Démarche à suivre
Voici comment tu peux trouver ces points :
1. **Calcule la dérivée de la fonction** : La dérivée te donne la pente de la tangente en tout point de la fonction.
2. **Égalise la dérivée à la pente donnée** : Résous l’équation pour trouver les valeurs de \( x \) où la dérivée est égale à la pente désirée.
3. **Trouve les points correspondants** : Une fois que tu as les valeurs de \( x \), trouve les coordonnées \( y \) correspondant sur la courbe initiale.
Pourquoi cette méthode fonctionne
Cette méthode fonctionne parce que la dérivée d’une fonction en un point donné représente la pente de la tangente à la courbe en ce point. Donc, en trouvant où la dérivée est égale à une certaine valeur, tu trouves les points où la tangente a cette pente spécifique.
Exemple d’application
Considérons la fonction \( f(x) = x^3 – 3x \). Trouvons les points où la pente de la tangente est égale à 3.
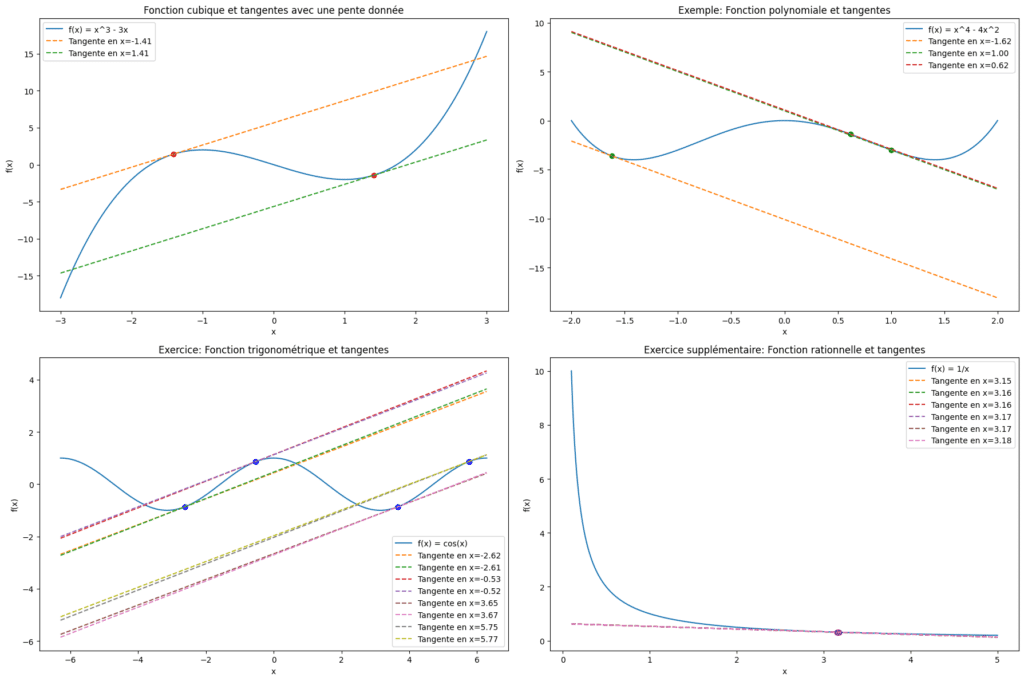
1. La dérivée de \( f(x) \) est \( f'(x) = 3x^2 – 3 \).
2. On résout l’équation \( 3x^2 – 3 = 3 \), ce qui donne \( x^2 = 2 \), soit \( x = \pm\sqrt{2} \).
3. Les points correspondants sur la courbe sont \( (\sqrt{2}, (\sqrt{2})^3 – 3\sqrt{2}) \) et \( (-\sqrt{2}, (-\sqrt{2})^3 + 3\sqrt{2}) \).
Exercices
À toi de jouer ! Voici quelques exercices pour t’entraîner à trouver les points où la tangente a une pente donnée.
Exercice 1
Trouve les points sur la courbe \( f(x) = x^4 – 4x^2 \) où la tangente a une pente de -4.
Voir la correction
1. La dérivée de \( f(x) = x^4 – 4x^2 \) est \( f'(x) = 4x^3 – 8x \).
2. On résout l’équation \( 4x^3 – 8x = -4 \), ce qui donne après simplification et résolution : \( x \approx 1.67 \) (solution réelle approximative).
3. Le point correspondant est trouvé en remplaçant \( x \) dans \( f(x) \).
Exercice 2
Trouve les points sur la courbe \( f(x) = \cos(x) \) où la tangente a une pente de 0.5.
Voir la correction
1. La dérivée de \( f(x) = \cos(x) \) est \( f'(x) = -\sin(x) \).
2. On résout l’équation \( -\sin(x) = 0.5 \), ce qui donne \( x \approx -1.13 + k\pi \) (où \( k \) est un entier), par approximation numérique.
3. Les points correspondants sont trouvés en remplaçant \( x \) dans \( f(x) \).
Exercice 3
Trouve les points sur la courbe \( f(x) = \frac{1}{x} \) où la tangente a une pente de -0.1.
Voir la correction
1. La dérivée de \( f(x) = \frac{1}{x} \) est \( f'(x) = -\frac{1}{x^2} \).
2. On résout l’équation \( -\frac{1}{x^2} = -0.1 \), ce qui donne \( x \approx \pm 3.16 \).
3. Les points correspondants sont trouvés en remplaçant \( x \) dans \( f(x) \).










