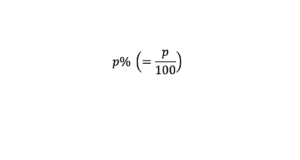Si tu as bien écouté en cours de spé maths, tu as du te rendre compte qu’il y a deux grandes notions en spé maths : les matrices et l’arithmétique. Trois articles ont été publiés récemment sur le site pour devenir le maître des matrices : les notions de base, le produit matriciel et enfin les matrices inversées.
Le jour du bac, les spé maths ont un exercice qui diffère par rapport à ceux qui ne font pas la spécialité maths. Cet exercice vaut généralement 5 points. Au début, les exercices de spé maths peuvent sembler un peu difficiles, mais c’est TOUJOURS la même chose. Un exercice qui mêle arithmétique et matrice et quasiment toujours de la même façon. Si tu ne nous crois pas, n’hésite pas à jeter un œil au corrigé détaillé de l’exercice de 2019 ici ou 2018 ici.
Venons en au cœur du sujet, les bases de l’arithmétique. En y regardant de plus près, tu connais déjà toutes les notions de base et tu les as vues au collège. Dit comme ça, ça fait réfléchir et pourtant je ne te mens pas. La division entière, la notion de diviseur commun, l’algorithme d’Euclide… tu as déjà entendu parler de tout ça. Alors pourquoi paniquer ? Aller on te réexplique tout cela !
Les bases de l’arithmétique : la division euclidienne dans \(\mathbb{Z}\)
La division euclidienne c’est la division entière. Oui oui, celle qu’on t’a enseignée en primaire. C’est une division de nombres entiers positifs ou négatifs par un autre nombre entier. Dans cette division, il n’y a pas de virgule dans le résultat, mais il y a un reste.
Soient \(a,b \in \mathbb{Z}\), alors il existe un unique couple \((q,r) \in \mathbb{Z}\) tel que $$a = bq+r$$.
On a forcément \(0 \leq r <b\).
q est le quotient de la division euclidienne de a par b.
r est le reste de la division euclidienne de a par b.
a est le dividende de la division euclidienne de a par b.
b est le diviseur de la division euclidienne de a par b.
Exemple : on veut faire la division euclidienne de 2020 par 3.
On obtient \(2020 = 3 * 673 + 1\)
673 est le quotient et 1 est le reste.
Les bases de l’arithmétique : les diviseurs
Si le reste de la division de a par b est 0, avec a et b des entiers, alors on dit que a est divisible par b.
Cela revient à dire qu’il existe un entier \(k\), tel que \(a=kb\). Si tu regardes bien c’est l’écriture de la division euclidienne avec \(q=k\) et \(r=0\).
Il y a équivalence entre les propositions suivantes :
- a est divisible par b
- a est un multiple de b
- b est un diviseur de a
- b divise a
- il existe un entier \(k\), tel que \(a=kb\)
On a la propriété suivante : si b divise a alors -b divise également a.
Petite démonstration : si b divise a, alors il existe \(k \in \mathbb{Z}\), tel que \(a=kb\). On peut réécrire cette égalité comme \(a=(-k)(-b)\). Or si k est un entier alors -k est aussi un entier, et cela revient bien à écrire que -b divise a.
Exemple : 7 est un diviseur de 21. En effet, on peut écrire \(21=3 \times 7\), mais on peut aussi écrire \(21=(-3) \times (-7)\). Donc -7 est bien un diviseur de 21.
Les bases de arithmétique : les multiples
Si tu as compris ce qu’est un diviseur, alors cette phrase devrait te paraître d’une évidence folle.
Soient a et b deux entiers relatifs, alors a est un multiple de b si et seulement il existe un entier k tel que \(a=kb\). C’est l’égalité du paragraphe d’au dessus et c’est normal puisque l’on a dit qu’il y a équivalence entre b divise a et a est un multiple de b.
Reprenons l’exemple du paragraphe précédent, puisque \(21=3 \times 7\), on peut dire que 21 est un multiple de 3 mais aussi que 21 est un multiple de 7.
Quelques propriétés
On a déjà dit que si b divise a alors -b divise aussi a.
On a également que si a, b, c sont des entiers et que c divise a et c divise b, alors c divise toutes les combinaisons linéaires de a et b.
C’est à dire que c divise tous les nombres de la forme $ma+nb$ avec m et n des entiers.
Petite démonstration :
c divise a donc il existe un entier k tel que \(a=kc\).
c divise b donc il existe un entier k’ tel que \(b=k’c\).
On peut donc écrire $ma+nb=kc+k’c=(k+k’)c$.
Cela veut dire en particulier que c divise a+b et a-b.
Exemple 3 divise 18 et 27.
On a \(27-18=9\) et 3 divise bien 9.
De même \(27+18=45\) est on écrire que \(45=3 \times 15\). Donc 3 divise bien 15.
A toi de jouer
Question 1 : si j’écris la division euclidienne de 87 par 5 : \(87=5*17+2\).
Alors qui est le dividende ? le diviseur ? le quotient ? et le reste ?
Question 2 : est ce correct d’écrire la division euclidienne de 48 par 5 comme \(48 = 8*5+8\) ?
Question 3 : est ce que 45 est un diviseur de 5 ?
Question 4 : est ce que 6 est un multiple de 18 ?
Réponse 1 : 87 est le dividende, 17 le quotient, 5 le diviseur, 2 le reste.
Réponse 2 : NON, le reste doit être inférieur à 5, il faut écrire \(48 = 9*5+3\) .
Réponse 3 : NON, c’est 5 qui est un diviseur de 45. On ne peut pas trouver un entier k tel que \(5=k \times 25\).
Réponse 4 : NON, c’est 18 qui est un multiple de 6. On ne peut pas trouver un entier k tel que \(6=k \times 18\).
Voilà qui conclut cet article ! Tu es prêt pour passer à la suite et découvrir, les congruences, PGCD et PPCM.
N’hésite pas à t’entraîner en faisant les exercices de spé maths des sujets de bac des années précédentes.