La quadrature du cercle : même si cette expression est devenue synonyme d’une tâche impossible, il s’agit avant tout d’un véritable problème mathématique posé dès l’Antiquité. Construire un carré ayant exactement la même aire qu’un cercle donné, à l’aide de la seule règle non graduée et du compas : voilà le défi lancé aux géomètres depuis des millénaires. Entre tentatives historiques, démonstrations modernes et outils numériques, découvrons ensemble pourquoi cette question a fasciné autant de savants, et pourquoi elle reste aujourd’hui encore un symbole d’impossible… ou presque.
Qu’est-ce que la quadrature du cercle ?
La quadrature du cercle est un problème de géométrie classique qui consiste à construire un carré ayant exactement la même aire qu’un cercle donné, en n’utilisant que deux outils : la règle non graduée et le compas.
Autrement dit, il s’agit de transformer, par des moyens strictement géométriques, un disque de rayon r en un carré dont la surface est égale à celle du cercle.
Origines historiques du quadruple du cercle
Le problème de la quadrature du cercle remonte à la Grèce antique, où il a été formulé comme l’un des trois grands défis de la géométrie classique, aux côtés de la trisection de l’angle et de la duplication du cube.
Parmi les premiers penseurs à s’y être intéressés figure Anaxagore, philosophe présocratique du Ve siècle av. J.-C., qui aurait tenté de résoudre ce problème lors de son emprisonnement, y voyant un exercice autant intellectuel que spirituel. Les géomètres grecs, attachés aux règles strictes de la construction à la règle non graduée et au compas, ont poursuivi cette quête pendant des siècles, notamment à travers des travaux comme ceux d’Hippocrate de Chios, qui parvint à cadrer des figures proches du cercle, les lunules.
Ce n’est qu’en 1882 que le mathématicien allemand Ferdinand von Lindemann mit un terme définitif à cette recherche en prouvant que π est un nombre transcendant, c’est-à-dire qu’il n’est solution d’aucune équation polynomiale à coefficients entiers. Cette découverte implique qu’il est impossible de construire géométriquement un carré de même aire qu’un cercle donné, avec les seuls outils autorisés par la géométrie euclidienne. La quadrature du cercle, longtemps perçue comme un défi solvable, entrait alors dans le domaine de l’impossible.
La réponse numérique : sommes-nous condamnés à l’approximation ?
Essayons de résoudre ce problème numériquement : prenons un cercle de rayon 1 cm. Son aire, donnée par
\(A = \pi * r^2 \approx 3.14 cm^2\)
Un carré dont l’aire est égale à A a donc pour côté \(\sqrt{\pi} \approx \sqrt{3.14} \approx 1.77cm\)
Problème résolu !
Deux millénaires pour ça ? Et bien non… Nous avons procédé par approximation : d’abord dans l’aire du cercle, puis dans le calcul du côté du carré.
Numériquement ça ne fonctionne pas ! Essayons autrement…
La réponse géométrique : vers la résolution ?
Les premières traces de résolution d’un tel problème remontent à l’Egypte antique : le papyrus Rhind, papyrus de mathématique écrit par le scribe Ahmès aux alentours de -1540. Ahmès nous invite à prendre le diamètre d’un cercle, le diviser en 9 parties égales, et construire un carré à partir des \(\frac{8}{9} \) du diamètre.
Prenons un cercle de diamètre 1 cm : le carré du cercle sera donc égal à \(\frac{8}{9}\) cm.
\(A_{carré} = (\frac{8}{9})^2 \approx 0.79 cm^2 \) et \(A_{cercle}= \pi \times 0.5^2 \approx 0.785 cm^2\)
On a une première piste de résolution géométrique, mais encore une fois, cela ne répond pas à notre besoin d’exactitude.
Procédons autrement : prenons un cercle qu’on fait rouler d’un point A sur un point B sur demi-tour, on obtient le segment AB qu’on prolonge d’un rayon jusqu’en C. On construit un demi-cercle sur le segment AC et une perpendiculaire en B, le point d’intersection entre le demi-cercle et la perpendiculaire est le point D qui nous donne le segment BD, avec lequel on construit un carré qui semble avoir la même aire que le cercle de départ.
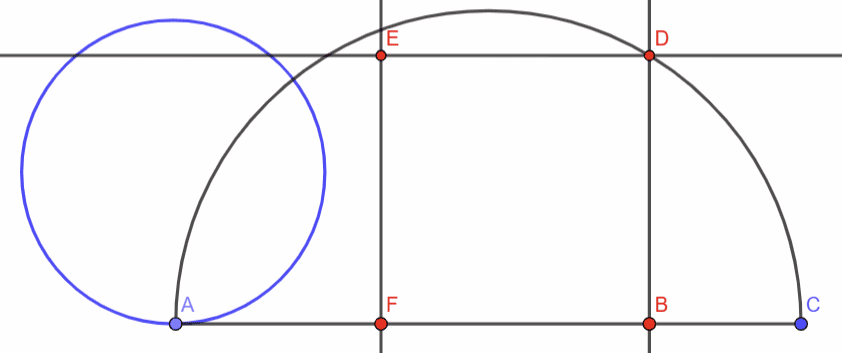
Vérification par le calcul : \( r = 1\) donc \( p = 2\pi \) donc \(AB = \pi \) et \(BC = 1\)
ADC est un triangle rectangle en D (rectangle inscrit dans un cercle dont un coté est le diamètre). ADB, DBC et ADC sont rectangles et similaires (puisqu’ils partagent leurs angles) : donc AB, DB et DA sont proportionnels à DB, CB et CD. Donc \(\frac{AB}{DB} = \frac{DB}{CB}\), donc \(\frac{\pi}{DB} = \frac{DB}{1}\) donc \(\pi \times 1 = DB^2 ⇔ DB = \sqrt{pi}\)
Ainsi : \(A_{carré} = \pi \) et \(A_{cercle} = \pi}\)
Cette construction est donc une quadrature du cercle parfaitement valide. Mais alors, comment a-t-on pu montrer en 1882 que la quadrature du cercle était un problème impossible ? Et bien parce que cette construction est correcte, mais ne respecte pas les critères d’une construction géométrique parfaite au sens des mathématiciens de l’Antiquité. En effet, pour correspondre aux règles de la construction géométrique parfaite, une figure doit être traçable au compas (cercle / arc de cercle) et à la règle (droite/segment) non graduée. Faire rouler le cercle comme on l’a fait est donc interdit !
Le problème de la quadrature du cercle est donc le suivant : construire géométriquement un carré ayant exactement la même aire qu’un disque donné à la règle non graduée et au compas. On peut généraliser cette question en se demandant ce qu’il est possible de construire à la règle et au compas, car c’est là que repose le cœur du problème !
On peut affirmer que tout entier naturel est constructible, leur somme et différence également. Grâce au théorème de Thalès, on peut affirmer que leur produit et leur quotient sont constructibles. On admet que la racine carrée d’un entier est également constructible. C’est en effet ce que nous dit le théorème de Wantzel dans sa version simplifiée : un nombre est constructible si et seulement si on peut l’écrire à partir de nombres entiers, de sommes, de différences, de produits, de quotients et de racines carrées.
On se demande donc si \(\pi \) est constructible : en bref, la réponse est non ! Pourquoi ? Car \(\pi \) est un nombre transcendant, c’est-à-dire qu’il n’est pas algébrique : il ne s’annule par aucun polynôme à coefficients rationnels, c’est ce que Ferdinand von Lindemann prouve en 1882.
La quadrature du cercle est donc impossible. Mais à quel point peut-on s’en rapprocher aujourd’hui ?
La résolution informatique : jusqu’où peut-on aller ?
Si la quadrature du cercle est mathématiquement impossible à réaliser avec une règle et un compas, elle devient numériquement approximable grâce aux outils informatiques. On peut donc tenter d’approximer la vérité en créant un algorithme Python tout simple !
C’est justement ce que tu apprends (ou apprendras) en terminale dans ton chapitre sur la programmation : une valeur exacte (comme \(\pi \)) ne peut pas toujours être atteinte par le calcul, mais les algorithmes permettent d’en donner une valeur approchée avec un niveau de précision contrôlé.
👉🏻 Premier exemple – Calcul simple de la longueur du côté d’un carré équivalent à un cercle de rayon donné.
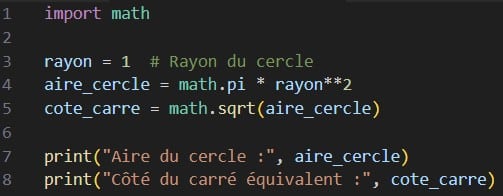
Ce programme simple calcule l’aire du cercle et déduit le côté d’un carré ayant la même aire. Il repose sur les formules classiques et sur la valeur de math.pi fournie par la bibliothèque Python. Mais ici, aucun contrôle n’est fait sur la précision ou l’erreur : c’est une simple évaluation.
👉🏻 Deuxième exemple – Approche itérative avec contrôle de la précision.
Ce deuxième programme utilise une boucle while pour améliorer progressivement l’approximation de la racine carrée de \(\pi \). L’algorithme s’arrête lorsque l’écart entre \(x^2 \) et \(\pi \) devient inférieur à une précision choisie (ici, \(10^6 \)).
On voit bien ici que l’informatique ne « résout » pas la quadrature du cercle au sens mathématique, mais la rend manipulable : on peut ajuster le niveau de précision, mesurer l’erreur, et comprendre que toute valeur approchée est conditionnée par les limites du calcul numérique. La programmation permet donc d’approcher l’idéal inaccessible de la quadrature du cercle.