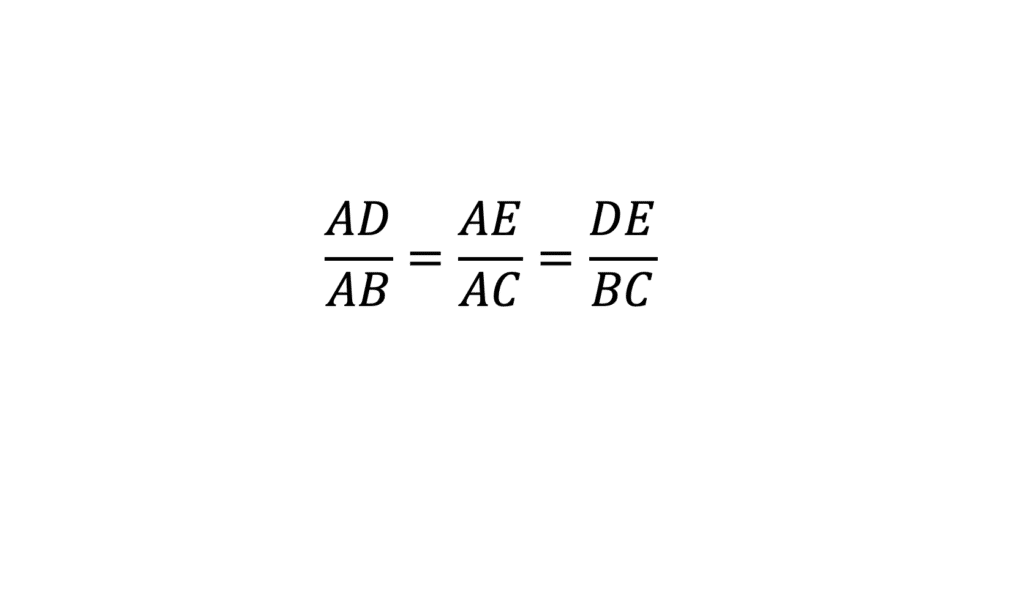Le théorème de Thalès, ça te dit quelque chose, non ? Que tu souhaites le découvrir ou simplement le réviser, tu es au bon endroit. Ce théorème est un incontournable du programme de collège et un outil essentiel pour cartonner au brevet.
C’est quoi le théorème de Thalès ?
Le théorème de Thalès concerne des relations de proportionnalité qui apparaissent lorsque des droites parallèles coupent deux droites sécantes. Il peut être formulé ainsi :
Soit un triangle \( ABC \). Si :
- Les points \( A\), \(D\) et \(B\) sont alignés sur la droite \( (AB) \).
- Les points \(A\), \(E\) et \(C\) sont alignés sur la droite \( (AC) \).
- Les droites \((DE)\) et \((BC)\) sont parallèles.
Alors, les rapports des longueurs des segments correspondants sont égaux : \( \frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC} \)
Cela signifie que les longueurs des segments sont proportionnelles. On peut aussi écrire cette égalité sous cette forme : \( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \).
⚠️ Attention : Les conditions \( (DE) \parallel (BC) \) et l’alignement des points sont indispensables pour appliquer ce théorème. N’oublie pas de les mentionner dans tes rédactions, sinon tu risques de perdre des points !
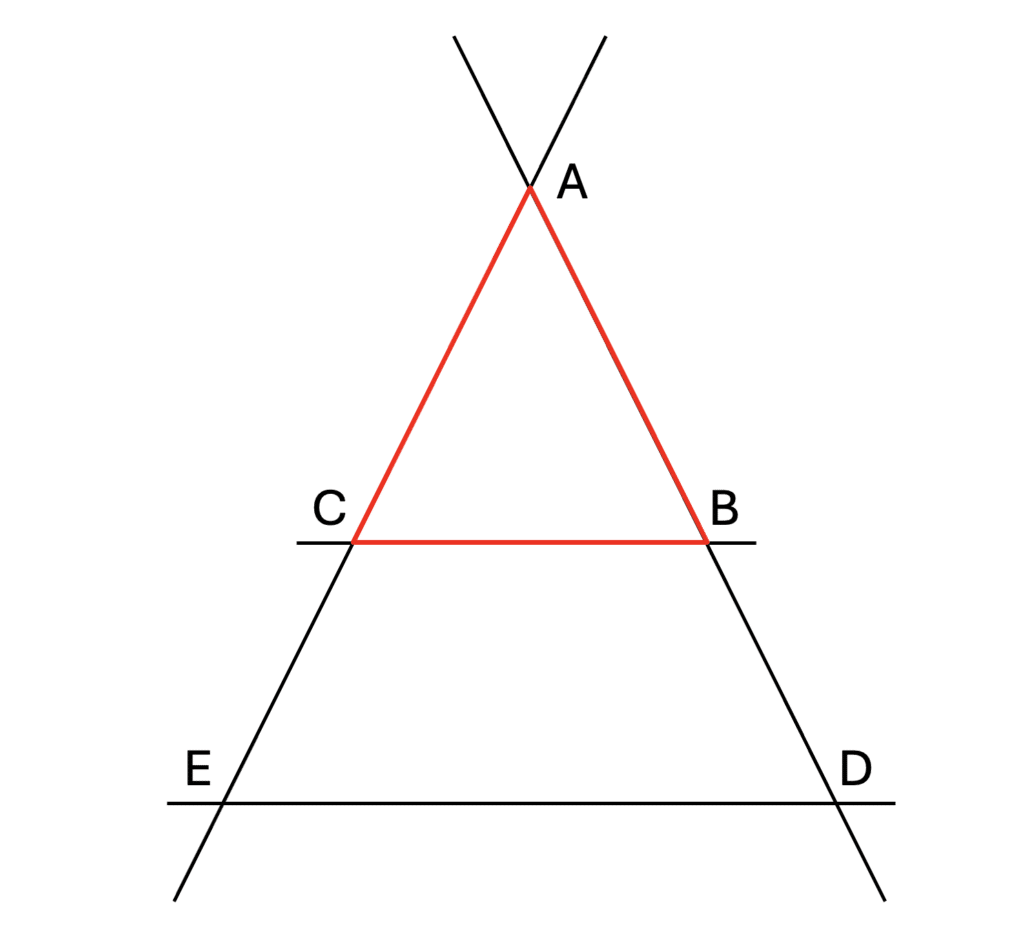
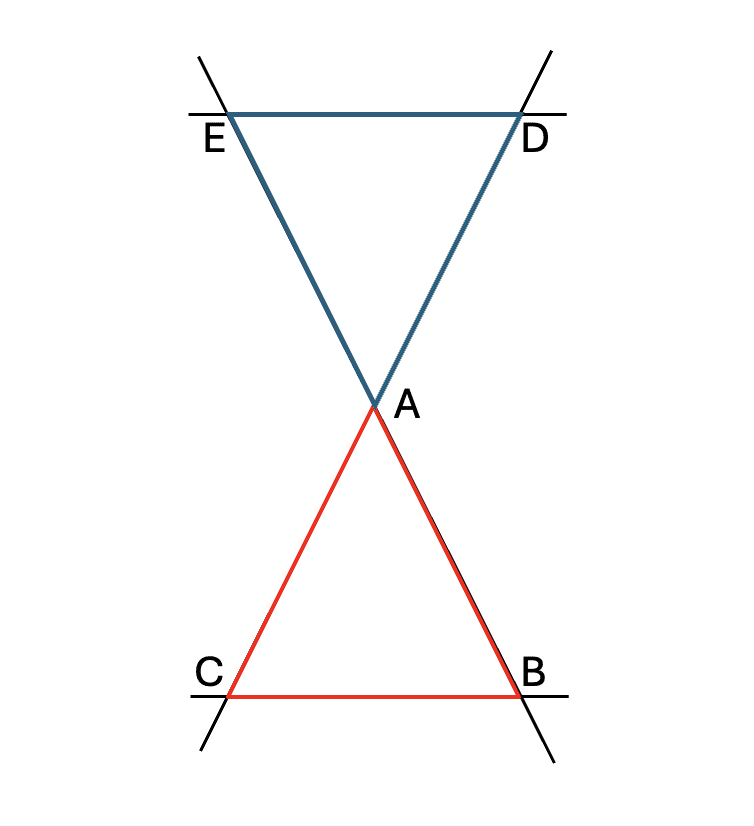
Les configurations principales du théorème de Thalès
Le théorème de Thalès peut s’appliquer dans deux situations principales, pour mieux illustrer cette configuration, voici une représentation schématique qui te permettra de visualiser clairement la situation.
Comment calculer une longueur avec le théorème de Thalès
Prenons un exemple pour voir comment le théorème de Thalès marche en pratique.
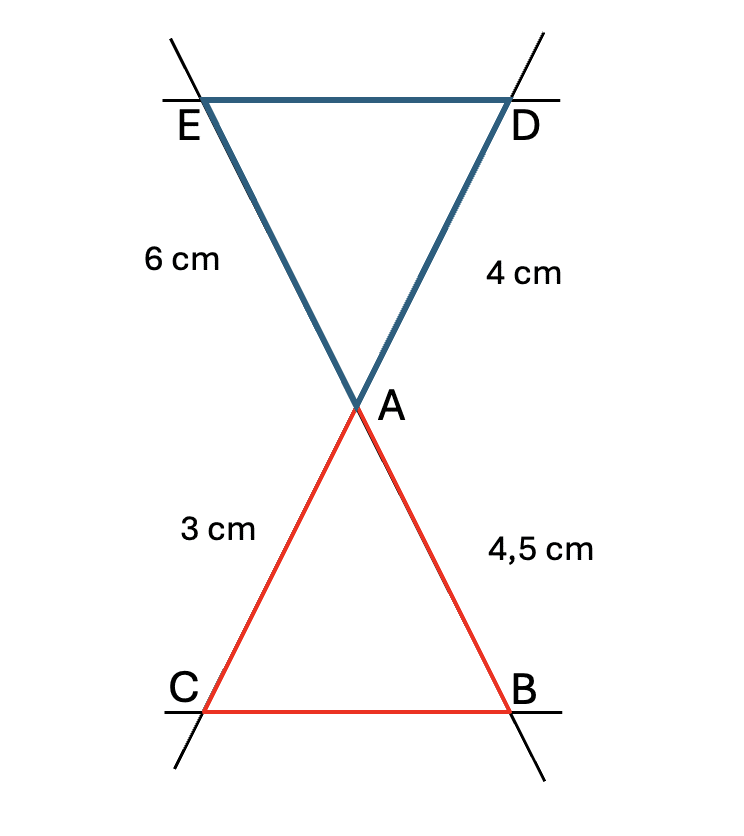
👉🏻 Exemple : Dans le triangle \( ABC \), les points \( E \) et \( D \) sont respectivement sur les droites \( (AC) \) et \( (AB) \) , avec \( (ED) \parallel (CB) \). On a :
- \( AD = 4 \text{ cm}. \)
- \( AC = 3 \text{ cm}. \)
- \( AE = 4,5 \text{ cm}. \)
Trouve la longueur de \( AB \).
Solution – Théorème de Thalès
Dans le triangle \( ABC \), les points \( D \) et \( E \) sont respectivement situés sur les droites \( (AB) \) et \( (AC) \), et la droite \( (ED) \) est parallèle à \( (BC) \). D’après le théorème de Thalès, on sait que : \( \frac{AD}{AB} = \frac{AE}{AC} \).
En remplaçant les valeurs données dans l’énoncé, on a : \( \frac{4}{AB} = \frac{4,5}{3} \).
On a \( AB = \frac{ 4 \times 3}{4,5} \approx 4,67 \), ainsi \( AB \approx 4,67 \text{ cm} \).
Vérifier que deux droites sont parallèles
Maintenant, voyons comment utiliser le théorème de Thalès pour prouver que deux droites sont parallèles.
👉🏻 Exemple : Les droites \( (BE) \) et \( (CD) \) sont sécantes en \( A \). On a :
- \( AB = 3 \text{ cm}. \)
- \( AE = 1 \text{ cm}. \)
- \( AD = 1,5 \text{ cm}. \)
- \( AC = 4,5 \text{ cm}. \)
Montre que \( (DE) \parallel (BC) \).
Solution – Théorème de Thalès
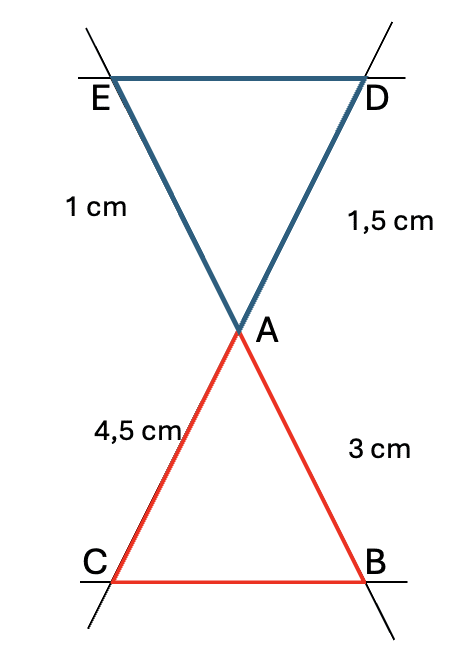
Les droites \( (BE) \) et \( (CD) \) sont sécantes en \( A \). Nous avons les informations suivantes : \( AB = 3 \, \text{cm} \), \( AE = 1 \, \text{cm} \), \( AC = 4,5 \, \text{cm} \), et \( AD = 1,5 \, \text{cm} \).
On commence par vérifier les rapports des segments. Calculons les rapports :
\( \frac{AB}{AE} = \frac{3}{1} = 3 \quad \text{et} \quad \frac{AC}{AD} = \frac{4,5}{1,5} = 3. \)
On constate que les deux rapports sont égaux :
\( \frac{AB}{AE} = \frac{AC}{AD}. \)
Les points \( A \), \( B \), et \( C \), ainsi que \( A \), \( B \), et \( E \), sont alignés.
Selon le théorème de Thalès, si ces rapports sont égaux, les droites \( (CB) \) et \( (ED) \) sont parallèles.
Par conséquent, les droites \( (CB) \) et \( (ED) \) sont parallèles.
Exercice – Théorème de Thalès (d’après Brevet des collèges Polynésie 2 septembre 2013)
Énoncé – Théorème de Thalès
🤔 Teiki se promène en montagne et aimerait connaître la hauteur d’un Pinus (ou Pin des Caraibes) situé devant lui. Pour cela, il utilise un bâton et prend quelques mesures au sol. Il procède de la façon suivante :
- Il pique le bâton en terre, verticalement, à 12 mètres du Pinus.
- La partie visible (hors du sol) du bâton mesure 2 m.
- Teiki se place derrière le bâton, de façon à ce que son œil, situé à 1,60 m au-dessus du sol, voie en alignement le sommet de l’arbre et l’extrémité du bâton.
- Teiki marque sa position au sol, puis mesure la distance entre sa position et le bâton. Il trouve alors 1,2 m.
On peut représenter cette situation à l’aide du schéma ci-dessous :
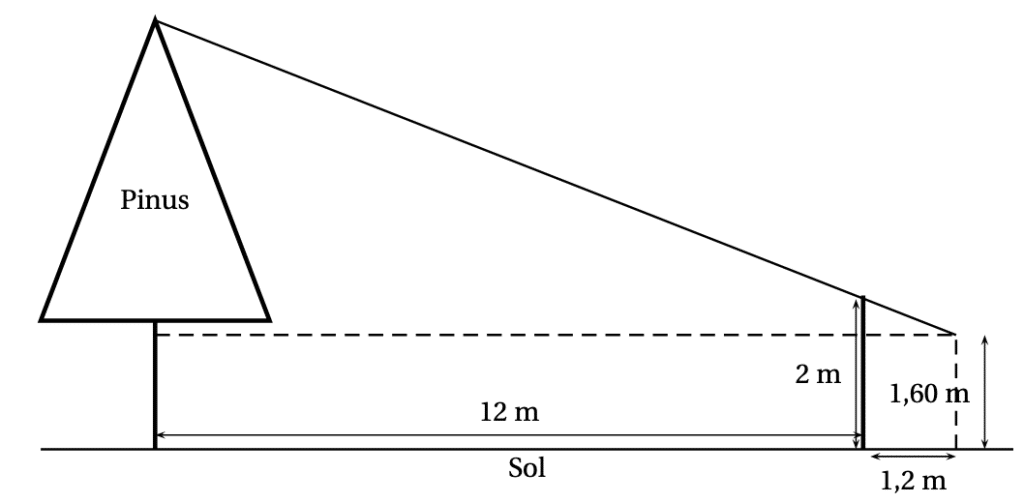
Quelle est la hauteur du Pinus au-dessus du sol ?
Solution – Théorème de Thalès
L’œil de Teiki, situé à 1,6 m au-dessus du sol, est aligné avec le sommet de l’arbre et l’extrémité du bâton. Le bâton et l’arbre sont parallèles car perpendiculaires au sol. La ligne de vision de Teiki forme un alignement, coupant ces deux droites parallèles (les troncs du bâton et de l’arbre). Cela permet d’appliquer le théorème de Thalès pour relier les distances et déterminer la hauteur de l’arbre.
D’après le théorème de Thalès, la proportion obtenue est :
\( \frac{H – 1,6}{0,4} = \frac{13,2}{1,2} \)
En résolvant cette proportion, on obtient :
\( H – 1,6 = \frac{13,2 \times 0,4}{1,2} = 4,4 \)
Ainsi, la hauteur totale de l’arbre est \( H = 4,4 + 1,6 = 6 \, \text{m} \).
La hauteur totale de l’arbre est donc de \( 6 \, \text{m} \).