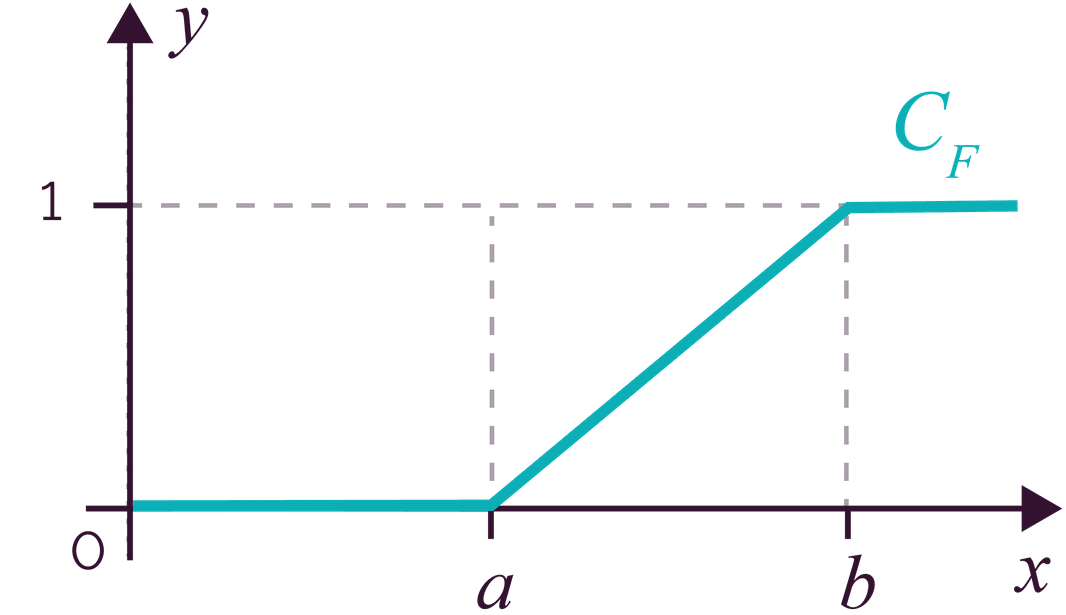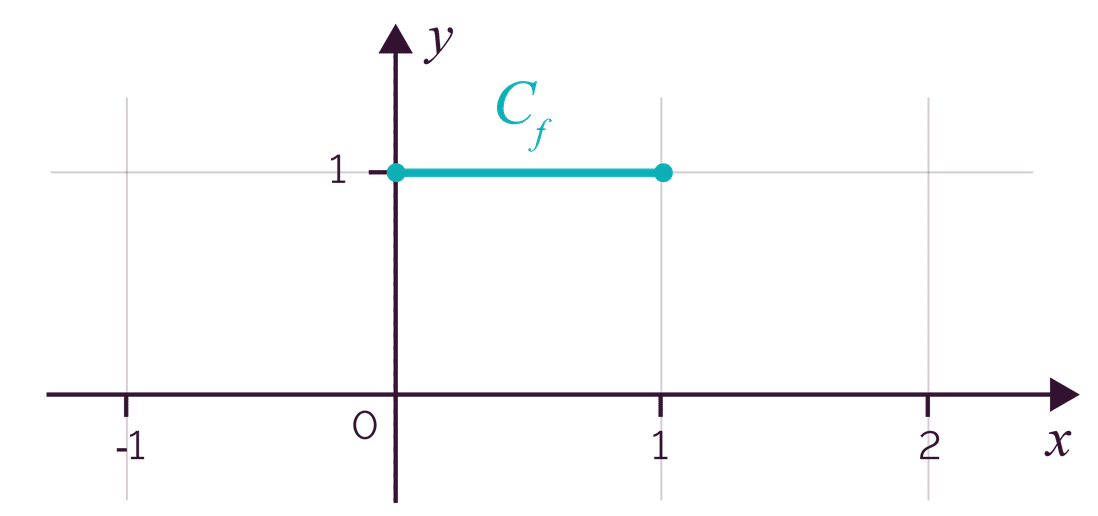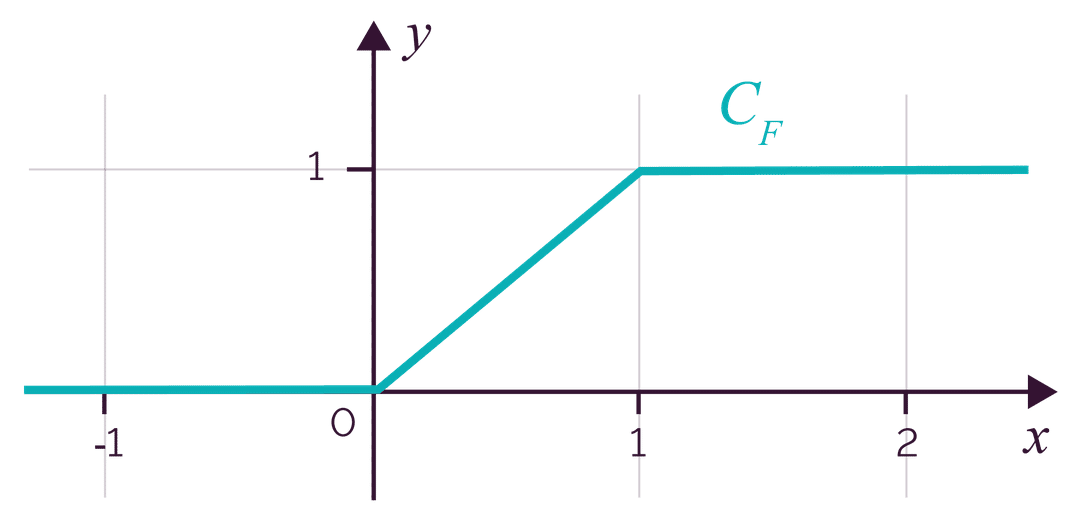Les variables aléatoires à densité sont une notion toute nouvelle sur les probabilités du programme de terminale. Une notion à ne pas négliger de part son importance !
Dans cet article, retrouve l’essentiel de ce qu’il faut savoir sur les variables aléatoires à densité.
Rappel sur les variables aléatoires à densité
On dit d’une variable aléatoire \(X\) qu’elle est continue si et seulement si sa fonction de répartition \(F_X\) est continue sur \(\mathbb {R}\). Les variables aléatoires continues sont diffuses : si \(X\) est une v.a. continue, alors pour tout \(x\) réel on a \(P(X = x) = 0\).
Soient \(X\) une variable aléatoire réelle et \(F_X\) sa fonction de répartition.
On dit que \(X\) est une variable aléatoire à densité lorsque \(F_X\) est continue sur \(\mathbb {R}\) et est de classe \(C_1\) sur \(\mathbb {R}\) sauf éventuellement en un nombre fini de points.
Si \(X\) est une v.a. à densité, on peut définir sur \(\mathbb {R}\) (sauf en un nombre fini de points) la fonction \(f_X : x \mapsto F’_X(x)\). On dit que c’est une densité de \(X\).
Lire aussi : Mathématiques : le produit scalaire
Loi uniforme à densité
\(a\) et \(b\) désignent deux nombres réels distincts.
On dit qu’une variable aléatoire \(X\) suit la loi uniforme sur l’intervalle \([a;b]\) lorsque sa densité de probabilité est une fonction constante sur \([a;b]\). On note alors : \(X \hookrightarrow \mathcal{U}([a,b])\).
La densité de probabilité de la loi uniforme sur \([a;b]\) est la fonction définie sur \([a;b]\) par \(
f(x) =
\begin{cases}
\frac{1}{b-a} &\text{si} \; a\le x\le b\\
0 &\text{sinon}
\end{cases}
\)
La fonction de répartition est donnée par \(
F(x) =
\begin{cases}
0 &\text{si} \; x < a\\
\frac{x-a}{b-a} &\text{si} \; a \le x < b\\
1 &\text{si} \; x \ge b
\end{cases}
\)
Soit \(X\) une variable aléatoire suivant la loi uniforme sur l’intervalle \([a;b]\). Pour tout intervalle \([c;d]\) inclus dans \([a;b]\), on a : \[P(c \le X \le d) = \displaystyle \int_{c}^{d} f(x) \, \mathrm{d}x = \frac {d-c}{b-a} \textrm{.}\]
Espérance et variance
Soit \(X\) une variable aléatoire suivant la loi uniforme sur l’intervalle \([a;b]\). On a alors :
\[E(X)=\frac{a+b}{2} \textrm{ et } V(X)=\frac{(a-b)^2}{12} \textrm{.}\]
Cas particulier où a=0 et b=1
Le cas particulier \(a =0\) et \(b = 1\) donne naissance à la loi uniforme standard, aussi notée \(\mathcal{U}([0;1])\).
Soit \(f\) la fonction définie sur \([0;1]\) par \(f(x) = 1\).
\(f\) est une fonction de densité de probabilité sur \([0;1]\).
Soit \(X\) une variable aléatoire de densité de probabilité \(f\).
On dit que \(X\) suit la loi uniforme sur \([0;1]\).
Si on note \F\) sa fonction de répartition sur \(\mathbb{R}\), alors : \(
F(x) =
\begin{cases}
0 &\text{si} \; x < 0\\
\frac{x-a}{b-a} &\text{si} \; x \in [0;1]\\
1 &\text{si} \; x > 1
\end{cases}
\)
Lire aussi : Le corrigé du bac 2022 de mathématiques
Exemple
Soit \(X\) une variable aléatoire qui suit la loi uniforme \(\mathcal{U}([3;6])\).
- Calculer \(P(3\le X \le 5,5)\).
- Calculer \(E(X)\).
- Calculer \(V(X)\).
Résolution :
\(f\) est définie sur \([2;5]\) par \(f(x)=\frac{1}{6-3} = \frac{1}{3}\).
- \( \begin{align}P(3\le X \le 5,5)&=\displaystyle \int_{3}^{5,5} \frac{1}{3} \, \mathrm{d}x\\
&=1,5*\frac{1}{3}\\&=\fbox{\(\frac{1}{2}\)}.\\\end{align}\) - \(E(X)=\frac{3+6}{2}=\fbox{\(\frac{9}{2}\)}.\)
- \(V(X)=\frac{(3-6)²}{12}=\frac{9}{12}=\fbox{\(\frac{3}{4}\)}.\)
Nous espérons que ce petit résumé de la loi uniforme à densité t’a plu ! N’hésite pas à aller regarder d’autres articles !