Dans cet article, tu vas retrouver le corrigé du premier sujet de bac de spécialité mathématiques 2025 ! Tu pourras ainsi te faire une idée de ta note à cette épreuve essentielle du baccalauréat ou bien t’entraîner si tu passes l’épreuve de spécialité mathématiques dans les prochains mois.
Bac 2025 : le sujet de l’épreuve de spécialité mathématiques
Tu peux retrouver ici l’ensemble des sujets des épreuves de spécialité du baccalauréat 2025 et n’oublies pas de revoir le programme de spécialité mathématiques :
Voici le sujet de l’épreuve de spécialité mathématiques du mardi 17 juin dernier :
Correction de l’exercice 1 – Sujet bac 2025 spécialité maths
L’exercice 1 portait sur un thème essentiel des mathématiques, celui des probabilités.
Question 1
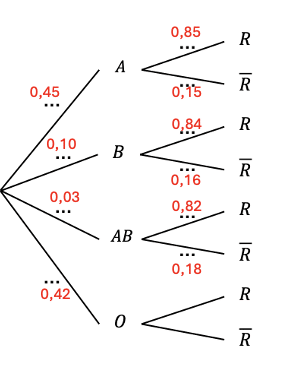
La majorité des probabilités était écrite dans l’énoncé sous forme de pourcentages. Pour les probabilités manquantes, les calculs sont les suivants :
- \( \displaystyle P(O) = 1 – P(A) – P(B) – P(A \cap B) = 1 – 0.45 – 0.10 – 0.03 = 0.42 \)
- \( \displaystyle P_B(\bar{R}) = 1 – 0.84 = 0.16 \)
- \( \displaystyle P_{AB}(\bar{R}) = 1 – 0.82 = 0.18 \)
- \( \displaystyle P_A(\bar{R}) = 1 – 0.85 = 0.15 \)
Question 2
On a :
\[ \displaystyle
P(B \cap R) = P(B) \times P_B(R) = 0{,}10 \times 0{,}84 = 0{,}084
\]
Dans le contexte de l’exercice, cela signifie que 8,4% des individus appartiennent au groupe B et sont de rhésus positif.
Question 3
D’après la formule des probabilités totales, on a :
\[ \displaystyle
P(R) = P(A \cap R) + P(B \cap R) + P(AB \cap R) + P(O \cap R)
\]
D’où \( \displaystyle P(O \cap R) = P(R) – P(A \cap R) – P(B \cap R) – P(AB \cap R)
Or \( \displaystyle P(O \cap R) = P(O) \times P_O(R) = 0{,}42 \times P_O(R) \)
\( \displaystyle P_O(R) = \frac{P(O \cap R)}{P(O)} = \frac{P(R) – P(A \cap R) – P(B \cap R) – P(AB \cap R)}{0{,}42} \)
\( \displaystyle P_O(R) = \frac{0{,}8397 – 0{,}45 \times 0{,}85 – 0{,}084 – 0{,}03 \times 0{,}82}{0{,}42} \)
\( \displaystyle P_O(R) = \frac{0{,}3486}{0{,}42} \)
\( \displaystyle P_O(R) = 0,83 \)
👉🏻 Tu as besoin d’un petit coup de pouce en mathématiques sur les racines carrées ou sur la fonction valeur absolue ? Jette un coup d’œil à nos articles sur tout ce qu’il faut savoir sur les racines carrées ou sur tout ce qu’il faut connaître sur la valeur absolue 👈🏻
Question 4
On doit trouver la probabilité de \( P(A \cap R) \). Or :
\( \displaystyle P(A \cap R) = P(O) \times P_O(R) \)
\( \displaystyle P(A \cap R) = P(O) \times (1 – P_O(R)) \)
\( \displaystyle P(A \cap R) = 0{,}42 \times (1 – 0{,}83) \)
\( \displaystyle P(A \cap R) = 0{,}0714 \)
La probabilité qu’un individu choisi au hasard dans la population française soit donneur universel est donc bien de 0,0714.
Question 5
a) Dans cette collecte de sang, on répète 100 fois la même expérience aléatoire de manière identique et indépendante les unes des autres puisque les personnes sont indépendantes. Il y a deux aussi possible dans cette expérience dont le succès est être un donneur universel, de probabilité \( p = 0,0714 \). La variable \( X \) compte le nombre de succès de cette expérience.
Donc \( X \) suit bien une loi binomiale de paramètres \( n = 100 \) et \( p = 0{,}0714 \).
b) \( \displaystyle P(X \leq 7) \approx 0{,}577 \)
c) Comme X suit une loi binomiale de paramètres \( n = 100 \) et \( p = 0{,}0714 \) on a :
- \( \displaystyle E(X) = n \times p = 100 \times 0{,}0714 = 7{,}14 \)
- \( \displaystyle V(X) = n \times p \times (1 – p) = 100 \times 0{,}0714 \times (1 – 0{,}0714) = 7{,}14 \times 0{,}9286 \approx 6{,}63 \)
Question 6
a) La variable aléatoire \( \displaystyle M_N \) représente la moyenne du nombre d’individus qui sont des donneurs universels sur les N collectes de sang réalisés
b) Par linéarité de l’espérance, on a :
\( \displaystyle
E(M_N) = E\left( \frac{1}{N} (X_1 + X_2 + \cdots + X_n) \right) = \frac{1}{N} \sum_{i=1}^{n} E(X_i) \)
Or pour tout i, on a \( E(X_i) = 7{,}14 \)
\( \displaystyle
E(M_N) = \frac{1}{N} \sum_{i=1}^{N} E(X_i) = \frac{1}{N} \times n \times 7{,}14 = 7{,}14
\)
Donc \( \displaystyle E(M_N) = 7,14 \)
c) De la même manière et grâce à l’indépendance des variables \( X_i \), on a :
\( \displaystyle V(M_N) = \frac{V(X)}{N} \)
\( \displaystyle V(M_N)= \frac{6{,}63}{N} \)
⚠️ Attention à ne pas faire d’erreur de rédaction, surtout dans les matières scientifiques ! ⚠️
d) On rappelle que l’inégalité de Bienaymé-Tchebychev, appliquée dans ce contexte, est:
\[ \displaystyle
P\left( \left| M_N – E(M_n) \right| \geq \varepsilon \right) \leq \frac{V(M_N)}{\varepsilon^2}
\]
Or on cherche à obtenir Or, on veut :
\[
P(7 < M_N < 7{,}28) \geq 0{,}95.
\]
Cette équation est équivalente à :
\[
P\big( |MN – 7{,}14| < \varepsilon \big) \geq 0{,}95.
\]
Pour \( t = 0,14 \), on a alors avec Bienaymé-Tchebychev \( P\big( |M_N – 7{,}14| > 0{,}14 \big) = 6{,}63 \times N \times 0{,}14^{2}. \)
D’où \[
\frac{16575}{49N} \leq 0,05.
\]
On obtient donc \( N \geq 6766 \).
La plus petite valeur de \( N \) telle que \( P(7 < M_N < 7{,}28) \geq 0{,}95 \)
est \( N = 6766. \)
Correction de l’exercice 2 – Sujet bac 2025 spécialité maths
Partie A : Lectures graphiques
Question 1
Le nombre dérivé \( f'(1) \) correspond à la pente de la tangente \( T_A \) à la courbe \( C_f \) au point A de coordonnées (1;2).
Or cette tangente passe par le point A(1;2) et par le point C(3;0). La pente est alors égale à :
\[ \displaystyle
\frac{x_C – x_A}{y_C – y_A} = \frac{3 – 1}{0 – 2} = \frac{2}{-2} = -1
\]
On obtient donc:
\[ \displaystyle
f'(1) = -1
\]
Question 2
Cette équation \( f'(x) = 0 \) signifie que la tangente à la courbe \( C_f \) est horizontale. Graphiquement, on observe qu’il y a alors deux solutions possibles.
Question 3
Au point \( x = 0,2 \), la courbe \( C_f \) est concave, donc on a \( \displaystyle f”(0{,}2) < 0 \). \( f”(0{,}2) \) est strictement négatif.
Partie B : Étude de la fonction \( f \)
Question 1
On a le discriminant donnée par :
\[
\Delta = (-3)^2 – 4 \times 2 \times 2 = 9 – 16 = -7
\]
Comme \( \Delta \) est strictement inférieur à 0, l’équation \( \displaystyle 2X^2 – 3X + 2 = 0 \) n’admet donc pas de solutions sur \( \displaystyle \mathbb{R} \).
Or pour savoir si la courbe \( C_f \) coupe l’axe des abscisses, il faut résoudre \( f(x) = 0 \). En choissisant \( X = ln(x) \), on retrouve bien l’équation initiale. Donc, l’équation \( f(x) = 0 \) n’a pas de solutions.
La courbe \( C_f \) ne coupe pas l’axe des abscisses.
Question 2
La fonction initiale ne nous permet pas de déterminer les limites car il y a des formes indéterminées. On la factorise donc :
\(
f(x) = x \left( 2 (\ln x)^2 – 3 \ln x + 2 \right)
\]
\[
f(x) = x (\ln x)^2 \left( 2 – \frac{3}{\ln x} + \frac{2}{(\ln x)^2} \right)
\]
Or on a :
\[
\lim_{x \to +\infty} x (\ln x)^2 = +\infty
\]
\[
\lim_{x \to +\infty} \left( 2 – \frac{3}{\ln x} + \frac{2}{(\ln x)^2} \right) = 2
\]
Par produit des limites, on obtient donc \( \lim_{x \to +\infty} f(x) = +\infty \)
Question 3
a) On a \( f'(x) = 2(\ln x)^2 + \ln x – 1 \). On dérive alors:
\[ \displaystyle
f”(x) = 2 \cdot \left( 2 \ln x \cdot \frac{1}{x} \right) + \frac{1}{x}
= \frac{4 \ln x}{x} + \frac{1}{x}
= \frac{1}{x} (4 \ln x + 1)
\]
b) On cherche le signe de la dérivée seconde de la fonction \( f \), autrement dit le signe de \( f” \).
D’une part, comme \( x \in \, ]0; +\infty[ \), on a \( \frac{1}{x} > 0 \).
D’autre part, \[ \displaystyle
f”(x) = \frac{1}{x} (4 \ln x + 1) > 0 \quad \Longleftrightarrow \quad 4 \ln x + 1 > 0 \Longleftrightarrow \ln x > -\frac{1}{4} \quad \Longleftrightarrow \quad x > e^{-1/4}
\]
Donc la fonction \( f \) est concave sur l’intervalle \( \displaystyle \left] 0 ; e^{-1/4} \right[ \) et convexe sur l’intervalle \( \displaystyle \left[ e^{-1/4} ; +\infty \right[ \).
Le point d’inflexion vaut \( e^{-1/4} \approx 0{,}779 \)
c) La fonction \( f \) est convexe sur l’intervalle \( \displaystyle \left[ 1 ; +\infty \right[ \) car \( e^{-1/4} < 1 \). Donc la courbe \( C_f \) est au-dessus de la tangente \( T_B \) sur l’intervalle \( [1 ; +\infty[ \).
Partie C : Calcul d’aire
Question 1
On calcule \( y = f'(e)(x – e) + f(e) \) :
- \( f'(e) = 2(\ln e)^2 + \ln e – 1 = 2 \cdot 1^2 + 1 – 1 = 2 \)
- \( f(e) = e \)
Donc \( \text{La tangente } T_B \text{ a pour équation réduite : } y = 2x – e \).
Question 2
On réalise une intégration par partie. On a :
\[ \displaystyle
u(x) = \ln x \Rightarrow u'(x) = \frac{1}{x} \, dx
\quad \text{et} \quad
v(x) = x \, dx \Rightarrow v'(x) = \frac{x^2}{2}
\]
\[ \displaystyle
\int_1^e x \ln x \, dx = \left[ \frac{x^2}{2} \ln x \right]_1^e – \int_1^e \frac{x^2}{2} \cdot \frac{1}{x} \, dx
\int_1^e x \ln x \, dx = \left[ \frac{x^2}{2} \ln x \right]_1^e – \int_1^e \frac{x}{2} \, dx
\]
Or :
\[ \displaystyle
\left[ \frac{x^2}{2} \ln x \right]_1^e = \frac{e^2}{2} \cdot \ln e – \frac{1^2}{2} \cdot \ln 1 = \frac{e^2}{2} \cdot 1 – \frac{1}{2} \cdot 0 = \frac{e^2}{2}
\]
\[ \displaystyle
\int_1^e 2x \, dx = 2 \times \left[ \frac{x^2}{2} \right]_1^e = 2 \times \left( \frac{e^2}{2} – \frac{1}{2} \right) = \frac{e^{2} – 1}{4}
\]
On somme alors dans la fonction et on a :
\( \displaystyle \int_1^e x \ln x \, dx = \frac{e^2}{2} – \frac{e^{2} – 1}{4} = \frac{e^{2} + 1}{4} \)
Question 3
La partie hachuré correspond à \( \displaystyle A = \int_{1}^{e} \bigl(f(x) – (2x – e)\bigr) \, dx \)
Après calculs, on obtient
\( \displaystyle A = 2 \int_{1}^{e} x (\ln x)^2 \, dx – 3 \int_{1}^{e} x \ln x \, dx + \int_{1}^{e} e \, dx \)
\( \displaystyle A = \frac{3e^{2} – 5 – 4e}{4} \)
L’aire \( A \) vaut donc \( \frac{3e^{2} – 5 – 4e}{4} \) en unité d’aire.
Correction de l’exercice 3
Affirmation 1
Soit \( \vec{u} \) un vecteur directeur de
\[ \displaystyle
\begin{cases}
x = 3 – 2t \
y = 2 – t \
z = -1 + 3t
\end{cases}
\]
Alors on a le vecteur \( \displaystyle \vec{u} = (-2, \; -1, \; 3) \). Le vecteur \( \overrightarrow{AB} \) est colinéaire à \(\vec{u} \).
On vérifie si les points A et B appartiennent à la droite définie par
\[ \displaystyle
\begin{cases}
x = 3 – 2t \
y = 2 – t \
z = -1 + 3t
\end{cases}
\quad \text{avec } t \in \mathbb{R}.
\]
On a pour le point A,
\( \displaystyle x = 3 – 2t \Rightarrow -1 = 3 – 2t \Rightarrow 2t = 4 \Rightarrow t = 2 \)
D’où \( y = 2 – t = 2 – 2 = 0 \)
\( z = -1 + 3t = -1 + 3 \times 2 = -1 + 6 = 5 \)
Donc le point A appartient bien à la droite.
Pour le point B, on a :
\( \displaystyle x = 3 – 2t \Rightarrow 3 = 3 – 2t \Rightarrow 2t = 0 \Rightarrow t = 0 \)
\( y = 2 – t = 2 – 0 = 2 \)
\( z = -1 + 3t = -1 + 3 \times 0 = -1 \)
Donc le point B appartient bien à la droite.
Une représentation paramétrique de la droite \( (AB) \) est donc bien :
\[ \displaystyle
\begin{cases}
x = 3 – 2t \
y = 2 – t \
z = -1 + 3t
\end{cases}
\quad \text{avec } t \in \mathbb{R}.
\]
L’affirmation 1 est vraie.
Affirmation 2
\[ \displaystyle
\overrightarrow{AB} =
\begin{pmatrix}
4 \
2 \
-6
\end{pmatrix}
\quad \text{et} \quad
\overrightarrow{OA} =
\begin{pmatrix}
-1 \
0 \
5
\end{pmatrix}.
\]
Ces deux vecteurs ne sont pas colinéaires.
On calcule alors avec le vecteur normal \( \vec{n} \)
\[ \displaystyle
\vec{n} \cdot \overrightarrow{AB} = 4 \times 5 + 2 \times (-1) – 6 \times 1 = 20 – 4 – 6 = 10 \neq 0
\]
Le vecteur \( \vec{n} =
\begin{pmatrix}
5 \
-2 \
1
\end{pmatrix} \)
n’est pas normal au plan \( (OAB) \). L’affirmation 2 est fausse.
Affirmation 3
Comme les vecteurs directeurs de ces deux droites, les vecteurs \( \displaystyle
\vec{d} =
\begin{pmatrix}
1 \
-1 \
2
\end{pmatrix}
\quad \text{et} \quad
\vec{d’} =
\begin{pmatrix}
4 \
4 \
-6
\end{pmatrix}
\) ne sont pas colinéaires. Les droites (d) et (d’) ne sont pas parallèles. Il faut vérifier si elles sont sécantes.
On cherche alors s’il existe une solution au système suivant :
\[ \displaystyle
\begin{cases}
15 + k = 1 + 4s \
8 – k = 2 + 4s \
-6 + 2k = 1 – 6s
\end{cases}
\]
On obtient :
\[ \displaystyle
\begin{cases}
s = 2{,}5 \
s = 2{,}5 \
k = -4
\end{cases}
\]
Ce système admet donc une solution. On peut en conclure que les droites d et d’ sont sécantes, et donc qu’elles sont coplanaires.
L’affirmation 3 est fausse.
Affirmation 4
Soit J le projeté orthogonal de C sur le plan P. On a alors :
\[
x = 2 + t \]
\[ y = -1 – t \]
\[ z = 2 + t \]
\[ x – y + z + 1 = 0 \]
\[
x = 2 + t \]
\[ y = -1 – t \]
\[ z = 2 + t \]
\[ 2+t + 1+t + 2+t + 1 = 0
\]
\[ x = 2 – 2 = 0 \]
\[ y = -1 + 2 = 1 \]
\[ z = 2 – 2 = 0 \]
\[ 3t + 6 = 0 \]
\[ t = -2 \]
Donc les coordonnées de J sont (0 ; 1 ; 0). On calcule alors la distance JC :
\[
JC = \sqrt{(0 – 2)^2 + (1 – (-1))^2 + (0 – 2)^2} \]
\[ JC = \sqrt{4 + 4 + 4} \]
\[ JC = \sqrt{12} \]
\[ JC = 2 \sqrt{3} \]
\]
La distance du point \( C(2, \, -1, \, 2) \) au plan \( P \) est égale à \( 2 \sqrt{3} \). L’affirmation 4 est vraie.
Correction de l’exercice 4
Partie A : étude d’un modèle discret
Question 1
On a \( u_0 = 1 \) et
\[
u_1 = -0,02 u_0^2 + 1,3 u_0 = -0,02 \times 1^2 + 1,3 \times 1 = 1,28.
\]
D’après ce modèle, la posidonie au premier juillet 2025 devrait recouvrir 1,28 ha
Question 2
a) On pose \( P_n \) : ” \( \quad 1 \leq u_n \leq u_{n+1} \leq 20 \) “
Initialisation
Pour \( n = 0 \), on a : \( \quad 1 \leq u_0 \leq u_1 \leq 20 \) d’après la question 1. Donc l’affirmation \( P_0 \) est vraie.
On passe à l’Hérédité.
Supposons que la propriété est vraie pour un entier naturel \(n\), tel que :
\[ \quad 1 \leq u_n \leq u_{n+1} \leq 20 \]
Montrons alors que cette propriété est encore vraie au rang \( n + 1 \).
On constate d’abord que \( h(u_n) = u_{n+1} \)
Par hypothèse de récurrence, on a \[ \quad 1 \leq u_n \leq u_{n+1} \leq 20 \]
Comme h est croissante sur l’intervalle \( \displaystyle \left[ 0 ; 20 \right[ \), on a alors
\[ h(1) \leq h(u_n) \leq h(u_{n+1}) \leq h(20) \]
\[
1 \leq 1{,}28 \leq u_{n+1} \leq u_{n+2} \leq 18 \leq 20
\]
Donc l’affirmation est héréditaire
Ainsi, on a bien démontré par récurrence que pour tout entier naturel \(n\), on a :
\[ \quad 1 \leq u_n \leq u_{n+1} \leq 20 \]
b) Par le théorème des suites monotones, comme \( (u_n) \) est croissante et majorée d’après les résultats de la question 2)a), alors cette suite converge.
c) On utilise le théorème du point fixe et on résout \( h(x) = x \), autrement dit \( -0,02 x^{2} + 1,3 x = x \).
On trouve alors \( x = 0 \) ou \( x = 15 \). 15 est l’unique solution appartenant à l’intervalle de solutions possibles.
Donc \( L = 15 \)
Question 3
a) Comme d’après la question 2)c), la limite de la suite \( u_n \) quand n tend vers l’infini est 15, autrement dit est supérieur au 14 hectare. Alors, on peut conclure que cela se produira.
b)
while u <= 14 :
n= n+1
u= -0.02*u**2 + 1.3*u
return n
Partie B : étude d’un modèle continu
Question 1
On a \( g(t) = \frac{1}{f(t)} \) d’où \( g« (t) = -\frac{f »(t)}{(f(t))^2} \).
\[ g'(t) = -\frac{0{,}02 f(t) (15 – f(t))}{(f(t))^2}.
\]
\[
g'(t) = -0{,}02 \cdot \frac{15 – f(t)}{f(t)}.
\]
\[
g'(t) = -0{,}02 \left( \frac{15}{f(t)} – 1 \right).
\]
Or \( g(t) = \frac{1}{f(t)} \), on obtient donc :
\[
g'(t) = -0{,}02 (15g(t) – 1) = -0{,}3g(t) + 0{,}02.
\]
\( g \) est bien solution de l’équation différentielle \( (E_2) : y’ = -0{,}3y + 0{,}02 \).
Question 2
Les solutions d’après le cours des équations différentielles de forme \( y’ = ay + b \),
sont données par :
\[
y(t) = Ce^{at} – \frac{b}{a},
\]
D’après la question 1, les solutions de l’équation différentielle \( (E_2) \) :
\[
y(t) = Ce^{-0{,}3t} – \frac{0{,}02}{-0{,}3} = Ce^{-0{,}3t} + \frac{1}{15}.
\] \( C \in \mathbb{R} \)
Question 3
On a \[
f(t) = \frac{1}{g(t)} = \frac{1}{\frac{14}{15}e^{-0{,}3t} + \frac{1}{15}}
= \frac{15}{14e^{-0{,}3t} + 1}.
\] car la seule solution qui vérifie \( g(0) = 1 \) est la fonction où \( C = \frac{14}{15} \). Il suffit de résoudre \( g(0) = \frac{1}{f(0)} \) = 1 \)
Question 4
On a \[
\lim_{t \to +\infty} (-0,3t) = -\infty
\].
D’où \[
\lim_{t \to +\infty} 14 e^{-0,3t} = 0
\lim_{t \to +\infty} \left( 14 e^{-0,3t} + 1 \right) = 1
\]
Par quotient, on a donc la limite de \( f \) à l’infini donnée par:
\[
\lim_{t \to +\infty} f(t) = \lim_{t \to +\infty} \frac{15}{14 e^{-0,3t} + 1} = \frac{15}{0 + 1} = 15.
\]
Question 5
On résout \( f (t) > 14 \), autrement dit \( \frac{15}{14 e^{-0,3t} + 1} > 14 \).
On trouve \( 15 > 196 e^{-0,3t} + 14 \) d’où \( \frac{1}{196} > e^{-0,3t} \). Puis on passe au logarithme et on trouve alors après calculs que :
\[
t > \frac{\ln(196)}{0.3}.
\]
\[
t > \frac{5.278}{0.3} \approx 17.59.
\]
car \( \ln(196) \approx 5.278 \)
Donc dans 17,59 années pour que la superficie recouverte par la posidonie dépassera 14 hectares.
Conclusion
Voilà, tu connais désormais tout la correction de ce premier sujet de mathématiques ! J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et lire cet article sur les techniques de conversion des unités de longueur !











