Dans cet article, tu vas retrouver la correction du second sujet de bac de spécialité mathématiques 2025 ! Tu pourras ainsi te faire une idée de ta note à cette épreuve essentielle du baccalauréat ou bien t’entraîner si tu passes l’épreuve de spécialité mathématiques dans les prochains mois.
Bac 2025 : le sujet de l’épreuve de spécialité mathématiques
Tu peux retrouver ici l’ensemble des sujets des épreuves de spécialité du baccalauréat 2025 et n’oublies pas de revoir le programme de spécialité mathématiques :
Voici le sujet du mercredi 18 juin de spécialité mathématiques :
Correction de l’exercice 1 – Bac 2025 spécialité maths
L’exercice 1 portait sur un thème essentiel des mathématiques, celui des probabilités.
Partie A
Question 1
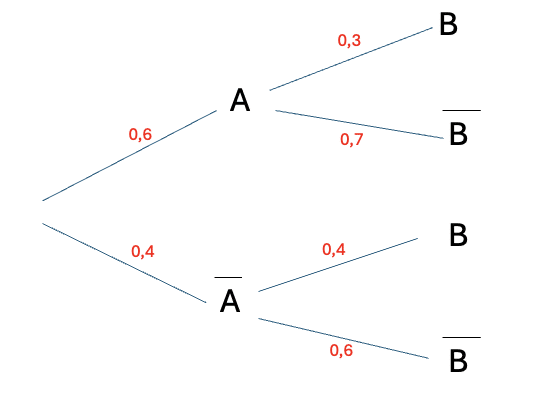
Question 2
On a :
\[ P(\overline{A} \cap \overline{B}) = P(\overline {A}) \times P(\overline{B} \cap \overline{B}) \]
\[ P(\overline{A} \cap \overline{B}) = 0{,}4 \times 0{,}6 = 0{,}24. \]
La probabilité que la personne ne chute pas pendant la première séance et pendant la deuxième séance est égale à 0,24.
Question 3
D’après la formule des probabilités totales, on a :
\[
P(B) = P( A \cap B) + P( A \cap \overline{B})
\]
\[
P(B) = 0{,}3 \times 0{,}6 + 0{,}4 \times 0{,}4 = 0{,}18 + 0{,}16
\]
\[
P(B) = 0{,}34
\]
La probabilité de l’évènement B est donc égale à 0,34.
Question 4
\[ \displaystyle
P(\overline{A} \mid \overline{B}) = \frac{P(\overline{A} \cap \overline{B})}{P(\overline{B})} = \frac{0{,}4 \times 0{,}6}{1 – 0{,}34} = \frac{0{,}24}{0{,}66} \approx 0{,}364.
\]
La probabilité que la personne n’ait pas chuté lors de la première séance sachant qu’elle ne chute pas pendant la deuxième séance est donc égale à 0,364.
👉🏻 Tu as besoin d’un petit coup de pouce en mathématiques sur les racines carrées ou sur la fonction valeur absolue ? Jette un coup d’œil à nos articles sur tout ce qu’il faut savoir sur les racines carrées ou sur tout ce qu’il faut connaître sur la valeur absolue 👈🏻
Question 5
a) On répète 100 fois la même expérience aléatoire de Bernoulli de manière identique et indépendante les unes des autres puisque les personnes sont indépendantes. Il y a deux aussi possible dans cette expérience dont le succès est « la personne n’a pas chuté aux deux séances » de probabilité \( p = 0,24 \). La variable \( X \) compte le nombre de succès de cette expérience.
Donc \( X \) suit bien une loi binomiale de paramètres \( n = 100 \) et \( p = 0{,}24 \).
b) Comme X suit une loi binomiale, on a :
\[
P(X \geq 20) = 1 – P(X < 20) = 1 – P(X \leq 19)
\]
Avec la calculatrice, on obtient
\[
P(X \geq 20) \approx = 0{,}855
\]
c) Comme X suit une loi binomiale de paramètres \( n = 100 \) et \( p = 0{,}24 \) on a :
- \( \displaystyle E(X) = n \times p = 100 \times 0{,}24 = 24 \)
Sur un échantillon de 100 personnes, on peut espérer attendre que 24 personnes ne chutent pas pendant la première et la deuxième séance.
Partie B
Question 1
Par linéarité de l’espérance,
\[
E(T) = E(T_1 + T_2) = E(T_1) + E(T_2)
\]
\[
E(T) = 40 + 60 = 100 \text{ minutes}.
\]
Le temps d’attente moyen d’une personne pour avoir accès aux activités sportives sur les deux jours est de 100 minutes.
Question 2
De la même manière et grâce à l’indépendance des variables \( T_1 \) et \( T_2 \), on a :
\( \displaystyle V(T) = V(T_1 + T_2) \)
\( \displaystyle V(T) = V(T_1) + V(T_2) \)
\( \displaystyle V(T)= 100 + 256 = 356 \)
⚠️ Attention à ne pas faire d’erreur de rédaction, surtout dans les matières scientifiques ! ⚠️
Question 3
v
On rappelle que l’inégalité de Bienaymé-Tchebychev, appliquée dans ce contexte, avec \( \varepsilon^2 = 40 \) est :
\[ \displaystyle
P\left( \left| T – E(T) \right| \geq \varepsilon \right) \leq \frac{V(T)}{\varepsilon^2}
\]
On obtient alors :
\[ \displaystyle
P\left( \left| T – 100 \right| \geq 40 \right) \leq \frac{356)}{40^2}
\]
Cette équation est équivalente à :
\[
P(60 \leq T \leq 140) \leq 0{,}2225.
\]
On obtient alors:
\[
1 – P(60 \leq T \leq 140) \geq 0{,}7775 > 0{,}77.
\]
Pour une personne choisie au hasard parmi celles venues un week-end au centre multisports, la probabilité que son temps total d’attente \( T \) soit strictement compris entre 60 et 140 minutes est donc bien supérieure à \( 0{,}77 \).
Correction de l’exercice 2
Partie A
Question 1
Les vecteurs directeurs de ces deux droites sont les vecteurs \( \displaystyle
\vec{d} =
\begin{pmatrix}
2 \
1 \
-1
\end{pmatrix}
\quad \text{et} \quad
\vec{d’} =
\begin{pmatrix}
1 \
1 \
-2
\end{pmatrix}
\).
On constate aisément que ces deux vecteurs ne sont pas colinéaires. Les droites (d) et (d’) ne sont pas parallèles. Il faut vérifier si elles sont sécantes.
On cherche l’existence d’une solution pour laquelle les deux équations paramétriques doivent être égales. On résout donc :
\[
\left\{
\begin{array}{l}
\frac{3}{2} + 2t = s \\
2 + t = \frac{3}{2} + s \\
3 – t = 3 – 2s
\end{array}
\right.
\iff
\left\{
\begin{array}{l}
-\frac{1}{2} + t = -\frac{3}{2} \\
s = 2 + t – \frac{3}{2} \\
t = 3 – 3 + 2s
\end{array}
\right.
\iff
\left\{
\begin{array}{l}
t = -1 \\
s = -0{,}5 \\
t = -1
\end{array}
\right.
\]
Or avec \( t = – 1 \) on retrouve dans le système correspondant à la représentation paramétrique de la droite (d). Les coordonnées suivantes :
\[
\left\{
\begin{array}{l}
x = -0,5 \\
y = 1 \\
z = 4
\end{array}
\right.
\]
Ces coordonnées correspondent à celles du point \( S \). On en conclut donc bien que les droites \( d \) et \( d’ \) sont sécantes au point \( S \left(-\frac{1}{2};\, 1;\, 4 \right) \).
Question 2
a) On calcule les coordonnées des deux vecteurs \( \vec{AB} \) et \( \vec{AC} \) à partir des coordonnées des points A, B et C.
\[
\vec{AB} = (1 – (-1);\, -1 – 2;\, 2 – 1) = (2;\, -3;\, 1).
\]
\[
\vec{AC} = (1 – (-1);\, 1 – 2;\, 1 – 1) = (2;\, -1;\, 0).
\]
Les coordonnées de ces deux vecteurs n’étant pas proportionnelles. Les vecteurs \( \vec{AB} \) et \( \vec{AC} \) ne sont pas colinéaires.
On s’intéresse alors à l’orthogonalité du vecteur \( \vec{n} \) par rapport à ces deux vecteurs.
\[
\vec{n} \cdot \vec{AB} = 1 \times 2 + 2 \times (-3) + 4 \times 1 = 0.
\]
\[
\vec{n} \cdot \vec{AC} = 1 \times 2 + 2 \times (-1) + 4 \times 1 = 0.
\]
Le vecteur \( \vec{n} \) est orthogonal à deux vecteurs non colinéaires du plan \( (ABC) \). On peut donc en conclure que le vecteur \( \vec{n} \) est un vecteur normal au plan \( (ABC) \).
b) D’après le résultat de la question précédent, on en déduit qu’avec le vecteur \( \vec{n}(1; 2; 4) \), l’équation du plan \((ABC) \) est alors
\[
1x + 2y + 4z + d = 0.
\]
Il faut déterminer la valeur de la variable \( d \). On utilise les coordonnées du point \( A(-1; 2; 1) \) appartenant à ce plan.
\[
1(-1) + 2(2) + 4(1) + d = 0
\]
\[
-1 + 4 + 4 + d = 0
\]
\[
d = -7.
\]
Une équation cartésienne du plan \( (ABC) \) est donc :
\[
x + 2y + 4z – 7 = 0.
\]
c) Il suffit de montrer que le point \( S \) n’appartient pas au plan \( (ABC) \) car les autres points A, B, C appartiennent par définition à ce plan. On utilise les coordonnées du point \( S \left( -\frac{1}{2};\, 1;\, 4 \right) \) dans l’équation du plan \( (ABC) \)trouvée à la question précédente:
\[
-\frac{1}{2} + 2 \times 1 + 4 \times 4 – 7 = -\frac{1}{2} + 2 + 16 – 7 = 10,5 \neq 0
\]
Le point \( S \) n’appartient donc pas au plan \( (ABC) \). Les points A, B, C, S ne sont pas coplanaires.
Question 3
a) Pour que H soit le projeté orthogonal de \( S \) sur le plan \( (ABC) \), il faut que le point H appartienne au plan \( (ABC) \) et que le vecteur \( \vec{SH} \) est colinéaire au vecteur normal \( \vec{n} \) du plan \( (ABC) \).
En remplaçant les coordonnées du point \( H \) dans l’équation du plan \( (ABC) \) on a :
\[ -1 + 2 \times 0 + 4 \times 2 – 7 = -1 + 0 + 8 – 7 = 0 \]
Donc H appartient au plan \( (ABC) \).
Les coordonnées du vecteur \(\vec{SH} \) sont \( \left(-\frac{1}{2};\, -1;\, -2 \right) \) car
\[ \left(-1 – \left(-\frac{1}{2}\right);\, 0 – 1;\, 2 – 4 \right) = \left(-\frac{1}{2};\, -1;\, -2 \right) \]
On remarque alors que \( \vec{SH} = -\frac{1}{2} \times \vec{n} \). Donc le vecteur \( \vec{SH} \) est colinéaire au vecteur normal \( \vec{n} \) du plan \( (ABC) \).
On en conclut donc bien que le point \( H \) est le projeté orthogonal de \( S \) sur le plan \( (ABC) \).
b) On calcule la distance SH en sachant que pour tout point \( M \) du plan \((ABC)\), la distance \( SM \) est toujours supérieure ou égale à la distance \( SH \).
\[ \displaystyle
SH = \sqrt{\left(-\frac{1}{2}\right)^2 + (-1)^2 + (-2)^2} = \sqrt{\frac{1}{4} + 1 + 4} = \sqrt{\frac{1}{4} + \frac{4}{4} + \frac{16}{4}} = \sqrt{\frac{21}{4}} = \frac{\sqrt{21}}{2}.
\]
Comme \( SM > SH \), Il n’existe aucun point \( M \) du plan \((ABC)\) tel que
\[
SM < \frac{\sqrt{21}}{2}.
\]
Partie B
Question 1
On a \( \overrightarrow{CM} = k \overrightarrow{CS}. \text{ Donc, on a }
\). Il faut alors résoudre :
\[
\begin{pmatrix}
x_M – x_C \\
y_M – y_C \\
z_M – z_C
\end{pmatrix}
= k
\begin{pmatrix}
x_S – x_C \\
y_S – y_C \\
z_S – z_C
\end{pmatrix}
\]
\[
\begin{pmatrix}
x_M – 1 \\
y_M – 1 \\
z_M – 1
\end{pmatrix}
=
\begin{pmatrix}
-\frac{3}{2}k \\
0 \\
3k
\end{pmatrix}
\]
On obtient alors le système suivant :
\[
\begin{cases}
x_M – 1 = -\frac{3}{2}k \\
y_M – 1 = 0 \\
z_M – 1 = 3k
\end{cases}
\quad \Rightarrow \quad
\begin{cases}
x_M = -\frac{3}{2}k + 1 \\
y_M = 1 \\
z_M = 3k + 1
\end{cases}
\]
Les coordonnées du point \( M \) en fonction de \( k \) sont donc \(
\left(-\frac{3}{2}k + 1 ;\quad 1 ;\quad 3k + 1 \right)
\)
Question 2
On sait que le triangle \( MAB \) est rectangle en \( M \) si et seulement si le produit scalaire des vecteurs \( \vec{MA} \) et \( \vec{MB} \) est nul, donc si et seulement si :
\[
\vec{MA} \cdot \vec{MB} = 0.
\]
On commence par calculer les coordonnées \( \vec{MA} \) et \( \vec{MB} \) à partir des coordonnées des points A, B et M.
\[
\overrightarrow{MA} = \begin{pmatrix}
x_A – x_M \\
y_A – y_M \\
z_A – z_M
\end{pmatrix}
= \begin{pmatrix}
-1 – \left(1 – \frac{3}{2}k\right) \\
2 – 1 \\
1 – \left(1 + 3k\right)
\end{pmatrix}
= \begin{pmatrix}
-2 + \frac{3}{2}k \\
1 \\
-3k
\end{pmatrix}
\]
\[
\overrightarrow{MB} = \begin{pmatrix}
x_B – x_M \\
y_B – y_M \\
z_B – z_M
\end{pmatrix}
= \begin{pmatrix}
1 – \left(1 – \frac{3}{2}k\right) \\
-1 – 1 \\
2 – \left(1 + 3k\right)
\end{pmatrix}
= \begin{pmatrix}
\frac{3}{2}k \\
-2 \\
1 – 3k
\end{pmatrix}
\]
On calcule alors le produit scalaire des deux vecteurs :
\[
\overrightarrow{MA} \cdot \overrightarrow{MB} = \left(-2 + \frac{3}{2}k\right)\left(\frac{3}{2}k\right) + (1)(-2) + (-3k)(1 – 3k)
\]
D’où \( \displaystyle \overrightarrow{MA} \cdot \overrightarrow{MB} = 0 \rightarrow \frac{45}{4}k^2 – 6k – 2 = 0 \quad \Rightarrow \quad 45k^2 – 24k – 8 = 0 \).
On calcule alors le discriminant de ce polynôme du second degré :
\[ \Delta = (-24)^2 – 4 \cdot 45 \cdot (-8) = 576 + 1440 = 2016 \]
Comme le discriminant est positif, il y a deux solutions qui sont
\[ \displaystyle
k_1 = \frac{4 – 2\sqrt{14}}{15} \quad \text{et} \quad k_2 = \frac{4 + 2\sqrt{14}}{15}.
\]
Or avec la calculatrice, on voit que seule la solution \( k_2 \) appartient à l’intervalle \( \left[0; 1\right] \).
Il existe donc un seul point \( M \) sur le segment \([CS] \) tel que le triangle \( MAB \) soit rectangle en \( M \).
Correction de l’exercice 3
Affirmation 1
On réécrit \( u_n \) en le factorisant par \( 5^n\) :
\[ \displaystyle
u_n = \frac{5^n \left( \frac{1}{5^n} + 1 \right)}{5^n \left( \frac{2}{3^n} + 1 \right)}
\]
\[ \displaystyle
u_n = \frac{5^n}{5^n} \cdot \frac{\frac{1}{5^n} + 1}{\frac{2}{3^n} + 1}
\]
\[ \displaystyle
u_n = \frac{1 + \left( \frac{1}{5} \right)^n}{1 + 2 \left( \frac{1}{3} \right)^n}
\]
Comme \(\frac{3}{5} \) est compris dans l’intervalle \(\left]-1;\,1\right[ \), on a :
\[
\lim_{n \to +\infty} \left(\frac{3}{5}\right)^n = 0.
\]
\[
\lim_{n \to +\infty} \left( \frac{1}{5} \right)^n +1 = 1.
\]
Or
\[
\lim_{n \to +\infty} \left( \frac{1}{5} \right)^n +1 = 0^+.
\]
D’où par quotient des limites,
\[
\lim_{n \to +\infty} u_n = +\infty.
\]
La suite \(u_n \) ne converge donc pas vers \( \frac{5}{3} \). L’affirmation 1 est fausse.
Affirmation 2
On raisonne par récurrence. On pose \( P_n \) : ” \( w_n \geq n \) “
Initialisation
Pour \( n = 0 \), on a : \( w_0 = 0 \). Or \( 0 \geq 0 \). Donc l’affirmation \( P_0 \) est vraie.
On passe à l’Hérédité.
Supposons que la propriété est vraie pour un entier naturel \(n\), tel que :
\[ w_n \geq n \]
Montrons alors que cette propriété est encore vraie au rang \( n + 1 \) tel que :
\[ w_{n+1} \geq n +1 \]
Par hypothèse de récurrence, on a :
\[ w_n \geq n \]
\[ 3 \times w_n \geq 3n \]
\[ 3w_n – 2n + 3 \geq 3n – 2n + 3 \]
\[ 3w_n – 2n + 3 \geq n + 3 \geq n + 1 \]
On a bien:
\[ w_{n+1} \geq n +1 \]
Donc l’affirmation est héréditaire
Ainsi, on a bien démontré par récurrence que pour tout entier naturel \(n\), on a :
\[ w_n \geq n \]
L’affirmation 2 est vraie.
Affirmation 3
Au point A, la tangente \( T \) traverse la courbe \( C_f \). Il y a un changement de convexité au point A, la fonction \( f \) est concave à ce point. Donc la fonction \( f \) n’est pas convexe sur tout son ensemble de définition.
L’affirmation 3 est fausse.
Affirmation 4
On pose une fonction \( h \) définie par \( h(x) = \ln(x) – x + 1 \) définie pour tout réel \( x > 0 \). On cherche le signe de cette fonction.
On a \( h« (x) = \frac{1}{x} – 1 \). On résout alors \( h »(x) = 0 \Longleftrightarrow x = 1 \).
Donc la dérivée \( h’ \) est positive sur \(]0,1[ \) et négative sur \(]1, +\infty[\)
La fonction \( f \) est croissante sur \(]0,1[ \), décroissante sur \(]1, +\infty[\) et atteint son maximum en \( x = 1 \) qui vaut 0. Donc pour tout réel \( x > 0 \), \( h(x) \leq 0 \).
Pour tout réel \( x > 0 \), \( \ln(x) – x + 1 \leq 0 \). L’affirmation 4 est vraie.
Correction de l’exercice 4
Partie A
Question 1
D’après le graphique, on observe que le le chariot aura parcouru 15 mètres au bout de 2 secondes.
Question 2
La longueur minimale à prévoir pour la zone de freinage est de 22,8 mètres.
Question 3
On a \( d'(4{,}7) \approx 1 \). Dans le contexte de l’exercice, cela signifie qu’à l’instant t = 4,7 secondes, la vitesse du chariot est d’environ 1 mètre par seconde.
Partie B
Question 1
a)Les solutions d’après le cours des équations différentielles de forme \( y’ = ay + b \),
sont données par :
\[
y(t) = Ce^{at} – \frac{b}{a},
\]
Or ici
\[
y’ + 0{,}6\,y = 0 \Longleftrightarrow y’ = -0,6y
\]
Les solutions de l’équation différentielle \( (E’) \) :
\[
y(t) = Ce^{-0{,}6t}
\] \( C \in \mathbb{R} \)
b) On dérive la fonction \( g \) donnée et on trouve:
\[
g'(t) = e^{-0{,}6 t} – 0{,}6 t \times e^{-0{,}6 t}
\]
D’où
\[
g'(t) + 0{,}6\,g(t) = \left(e^{-0{,}6 t} – 0{,}6 t \times e^{-0{,}6 t}\right) + 0{,}6 \times \left(t \times e^{-0{,}6 t}\right)
\]
\[
g'(t) + 0{,}6\,g(t) = e^{-0{,}6 t} – 0{,}6 t \times e^{-0{,}6 t} + 0{,}6 t \times e^{-0{,}6 t}
\]
\[
g'(t) + 0{,}6\,g(t) = e^{-0{,}6 t}.
\]
La fonction \( g \) est une solution de l’équation différentielle \( E \).
c) D’après les résultats des deux questions précédentes, on a :
\[ \displaystyle
y(t) = C \, e^{-0{,}6 t} + t \, e^{-0{,}6 t}, \quad C \in \mathbb{R}
\]
d) D’après les résultats des questions précédentes, la fonction \( v \) est la solution spécifique de l’équation différentielle \(E \) qui satisfait la condition initiale \( v(0) = 12 \).
On a alors :
\[
v(t) = (C + t) \, e^{-0{,}6 t}.
\]
On cherche la valeur de la constante \( C \):
\[
v(0) = 12 \Longleftrightarrow C e^{0} + 0 = 12 \Longleftrightarrow C = 12.
\]
Pour tout réel \( t \) appartenant à l’intervalle \([0 ; +\infty[\), on a :
\[
v(t) = (12 + t) \times e^{-0{,}6 t}
\]
Question 2
a) On dérive la fonction \( v \) qui est dérivable sur \( \displaystyle \mathbb{R} \) comme somme et composés de fonctions qui le sont. On trouve:
\[
v'(t) = e^{-0{,}6 t} – 0{,}6 \times (12 + t) \times e^{-0{,}6 t}.
\]
D’où par factorisation,
\[
v'(t) = e^{-0{,}6 t} \times \left[ 1 – 0{,}6 \times (12 + t) \right]
\]
\[
v'(t) = (-6{,}2 – 0{,}6 t) \times e^{-0{,}6 t}.
\]
b) On a \( v(t) = 12 \times e^{-0{,}6 t} + t \times e^{-0{,}6 t} \)
Or
\[
\lim_{t \to +\infty} 12 \times e^{-0{,}6 t} = 0.
\]
Et par croissances comparées, on a :
\[
\lim_{t \to +\infty} t \times e^{-0{,}6 t} = 0
\]
On en conclut par somme,
\[
\lim_{t \to +\infty} v_n = 0
\]
c) Comme \( e^(-0,6t) > 0 \) alors la fonction \( v’ \) est du signe de \( (-6,2 – 0,6t) \).
\[
-6,2 – 0,6t = 0 \Longleftrightarrow -0,6t = 6,2 \Longleftrightarrow t = \frac{6{,}2}{-0{,}6} \Longleftrightarrow t < 0
\]
Donc \( v’ < 0 \). La fonction \( v \) est strictement décroissante pour tout réel \( x \geq 0 \). On a alors le tableau de variations suivant :
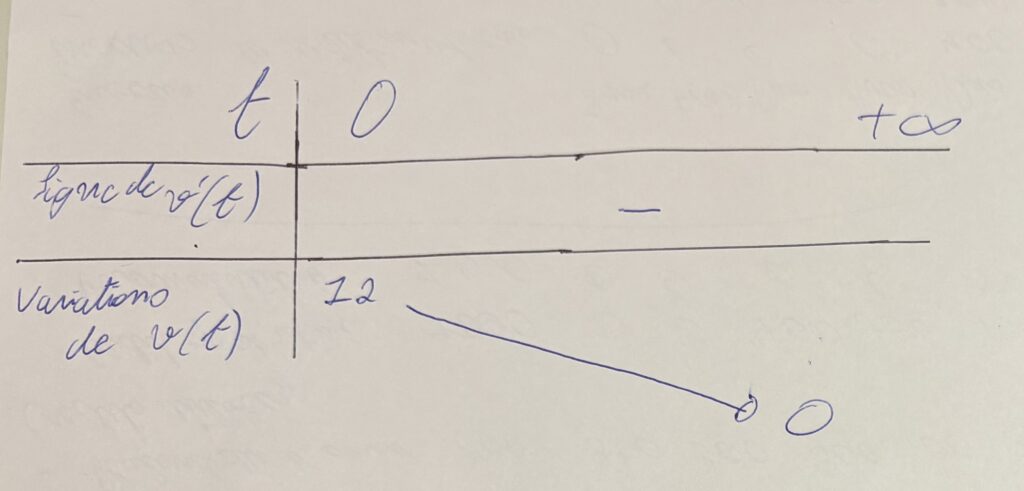
d) Pour tout réel \( x \geq 0 \), on observe que :
- La fonction \( v \) est continue (car dérivable)
- La fonction \( v \) est strictement décroissante
- \( v(0) = 12 \) et \( \lim_{t \to +\infty} v_n = 0 \)
D’après le corollaire du théorème des valeurs intermédiaires, l’équation \( v(t) = 1 \) admet donc une unique solution \( \alpha \in ]0, +\infty[ \) avec \( \alpha \approx 4{,}7 \).
Question 3
Le système se déclenche lorsque la vitesse \( v(t) \) atteint ou passe en dessous de 1 mètre par seconde, autrement dit quand \( v(t) \leq 1 \).
Or \( v(t) \leq 1 \Longleftrightarrow t \geq \alpha \).
Donc \( t \approx 4{,}7 \) secondes.
Le système se déclenche à partir d’environ 4,7 secondes.
Partie C
Question 1
On réalise une intégration par partie. On a :
\[ \displaystyle
u(x) = 12 + x \Rightarrow u'(x) = 1 \, dx
\quad \text{et} \quad
v(x) = e^{-0{,}6 t} \, dx \Rightarrow v'(x) = \frac{e^{-0{,}6 t}}{-0{,}6}
\]
\[ \displaystyle
\int_1^t (12 + x) e^{-0{,}6 t} \, dx = \left[ (12 + x) \times \frac{e^{-0{,}6 t}}{-0{,}6} \right] – \int_1^t \times \frac{e^{-0{,}6 t}}{-0{,}6} \, dx
\]
On obtient :
\[ \displaystyle
\int_1^t (12 + x)e^{-0{,}6 t} \, dx = \left[\frac{(12+x)e^{-0{,}6 t}}{-0{,}06}\right]_{0}^{t} + \frac{1}{0.6}\int_{0}^{t}e^{-0.06x}dx
\]
Après calculs on a donc :
\[ \displaystyle
\int_1^t (12 + x)e^{-0{,}6 t} \, dx = e^{-0{,}6 t} \frac{(8,2+0,6t)}{-0,36} + \frac{205}{9}
\]
\[ \displaystyle
\int_1^t (12 + x) e^{-0{,}6 t} \, dx = e^{-0{,}6 t} \times \left(-\frac{5}{3} t – \frac{205}{9} \right) + \frac{205}{9} \]
On a bien démontré l’expression demandée.
Question 2
D’après le résultat de la question 3 de la Partie B, il faut que \( t \approx 4{,}7 \) secondes pour que le système se déclenche. On a donc:
\[
d(4{,}7) = e^{-2{,}82} \times \left( -\frac{275{,}5}{9} \right) + \frac{205}{9}
\]
\[
d(4{,}7) \approx 20{,}95
\]
La distance parcourue est donc d’environ 20,95 mètres.
Conclusion
Voilà, tu connais désormais tout la correction de ce second sujet de mathématiques ! J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et lire cet article sur les techniques de conversion des unités de longueur !