Si tu cherches à mieux comprendre les puissances en maths, cet article est fait pour toi ! Tu les rencontreras dans presque tous les chapitres, des équations simples aux problèmes plus complexes. Au lycée, et surtout pour ton bac, maîtriser les puissances te sera super utile, que ce soit pour résoudre des équations, comprendre des fonctions, ou même pour analyser des données. Dans cet article, on va te guider à travers les règles essentielles à connaître et surtout, on va te montrer comment éviter les erreurs courantes qui peuvent te faire perdre des points. Prêt à devenir un pro des puissances et à impressionner tes profs ? Alors, c’est parti ! 🚀
Définition et explications des puissances
1.1 Introduction aux puissances
Imagine que tu as un sac de bonbons. Si chaque jour, tu reçois un nombre de bonbons égal à ce que tu avais la veille multiplié par un certain nombre, tu utilises sans le savoir les puissances ! Une puissance, c’est simplement une manière compacte d’écrire une multiplication répétée. Par exemple, si tu as 2 bonbons et que ce nombre double chaque jour pendant 3 jours, tu auras 2 × 2 × 2 bonbons, ce qu’on écrit 23 (on lit « 2 à la puissance 3 »).
Définition mathématique d’une puissance
Une puissance est définie par un nombre appelé la base (par exemple, 2) et un autre nombre appelé l’exposant (par exemple, 3). La puissance te dit combien de fois tu dois multiplier la base par elle-même. Donc, 23 signifie 2 multiplié par lui-même 3 fois : 2 × 2 × 2 = 8.
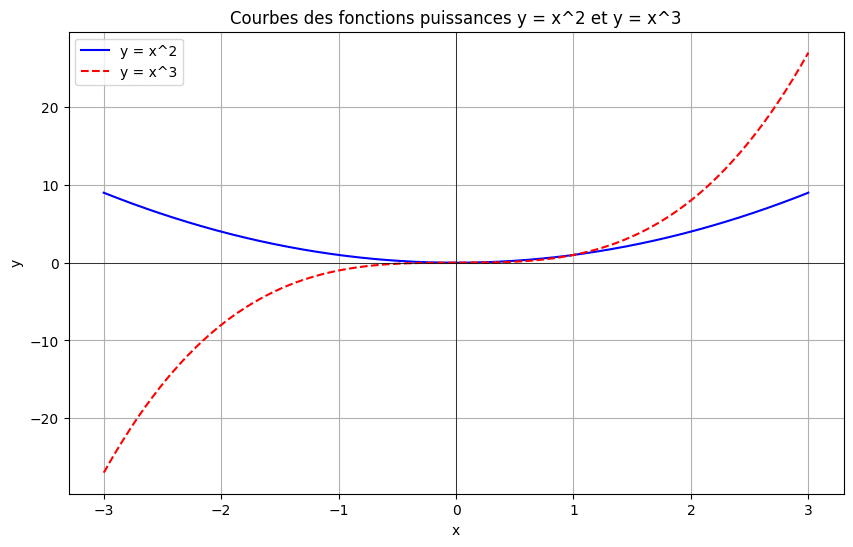
Sur ces graphes, tu peux voir comment la valeur de y change avec x pour différentes puissances. La courbe de y = x^2 est une parabole, tandis que celle de y = x^3 a une forme différente, avec une symétrie particulière.
Petit exercice pour vérifier la compréhension
Calcule les valeurs suivantes :
34, (-2)3 et (1/3)2
Voir la correction
Les erreurs fréquentes
2.1 Identifier les erreurs courantes
Imagine que tu essaies de résoudre un problème de maths et que tu confonds les règles des puissances. C’est comme si tu essayais de cuisiner sans savoir si tu dois ajouter du sucre ou du sel ! Voici quelques erreurs courantes que tu pourrais faire avec les puissances :
- Confusion entre addition et multiplication des exposants : Beaucoup de gens pensent que am + an est égal à am+n, mais ce n’est pas vrai ! La multiplication des exposants fonctionne différemment.
- Règles incorrectes pour les exposants négatifs : Certaines personnes pensent qu’un exposant négatif rend la base négative, mais en réalité, cela signifie que la base est l’inverse (par exemple, a-n = 1/an).
- Erreurs avec les puissances de 0 et de 1 : Tout nombre à la puissance 0 vaut 1, et à la puissance 1, il reste lui-même. Mais il est facile d’oublier ces règles simples !
Petit exercice pour vérifier la compréhension
Corrige les expressions suivantes si elles sont incorrectes :
- 32 + 33 = 35
- 4-2 = -16
- 70 = 0
Voir la correction
- Faux. 32 + 33 = 9 + 27 = 36, pas 35 (qui est 243).
- Faux. 4-2 = 1/(42) = 1/16.
- Faux. 70 = 1.
3. Les propriétés utiles et exercices d’application
Produit de puissances de même base
Quand tu multiplies deux puissances avec la même base, tu peux simplement ajouter leurs exposants. Par exemple, si tu as 23 × 24, cela revient à 23+4 = 27.
Quotient de puissances de même base
Quand tu divises deux puissances avec la même base, tu soustrais leurs exposants. Par exemple, 25 / 22 = 25-2 = 23.
Puissance de puissance
Quand tu as une puissance d’une puissance, tu multiplies les exposants. Par exemple, (23)2 = 23×2 = 26.
Puissance d’un produit et d’un quotient
Quand tu as une puissance d’un produit ou d’un quotient, tu peux distribuer l’exposant. Par exemple, (ab)3 = a3 × b3 et (a/b)3 = a3 / b3.
Exercice 1
Calcule les expressions suivantes :
- 24 × 23
- 75 / 73
- (32)4
- (5×2)3
Voir la correction
- 24 × 23 = 24+3 = 27 = 128
- 75 / 73 = 75-3 = 72 = 49
- (32)4 = 32×4 = 38 = 6561
- (5×2)3 = 53 × 23 = 125 × 8 = 1000
Les propriétés utiles et exercices d’application
3.1 Propriétés des puissances
Les puissances ont des propriétés incroyablement utiles qui peuvent te simplifier la vie en maths. Voici quelques-unes des plus importantes :
Produit de puissances de même base
Quand tu multiplies deux puissances avec la même base, tu additionnes simplement leurs exposants !
Exemple : \( a^m \times a^n = a^{m+n} \). Donc, si tu as \( 2^3 \times 2^4 \), c’est égal à \( 2^{3+4} = 2^7 = 128 \).
Quotient de puissances de même base
Quand tu divises deux puissances avec la même base, tu soustrais leurs exposants.
Exemple : \( a^m / a^n = a^{m-n} \). Donc, \( 3^5 / 3^2 = 3^{5-2} = 3^3 = 27 \).
Puissance de puissance
Quand tu as une puissance élevée à une autre puissance, tu multiplies les exposants.
Exemple : \( (a^m)^n = a^{m \times n} \). Donc, \( (2^3)^2 = 2^{3 \times 2} = 2^6 = 64 \).
Puissance d’un produit et d’un quotient
La puissance d’un produit est le produit des puissances. Par exemple, \( (a \times b)^n = a^n \times b^n \). Et pour un quotient, c’est similaire : \( (a / b)^n = a^n / b^n \).
Exemple : \( (2 \times 3)^3 = 2^3 \times 3^3 = 8 \times 27 = 216 \).
3.2 Exemples détaillés pour chaque propriété
Voici quelques exemples supplémentaires pour t’aider à bien comprendre chaque propriété :
- Produit : \( 5^2 \times 5^3 = 5^{2+3} = 5^5 = 3125 \)
- Quotient : \( 7^6 / 7^2 = 7^{6-2} = 7^4 = 2401 \)
- Puissance de puissance : \( (4^2)^3 = 4^{2 \times 3} = 4^6 = 4096 \)
- Puissance d’un produit : \( (3 \times 4)^2 = 3^2 \times 4^2 = 9 \times 16 = 144 \)
3.3 Exercices d’application
Exercice 1
Calcule \( 2^3 \times 2^4 \).
Voir la correction
\( 2^3 \times 2^4 = 2^{3+4} = 2^7 = 128 \)
Exercice 2
Calcule \( 5^6 / 5^3 \).
Voir la correction
\( 5^6 / 5^3 = 5^{6-3} = 5^3 = 125 \)
Exercice 3
Calcule \( (3^2)^3 \).
Voir la correction
\( (3^2)^3 = 3^{2 \times 3} = 3^6 = 729 \)
Exercice 4
Calcule \( (2 \times 5)^3 \).
Voir la correction
\( (2 \times 5)^3 = 2^3 \times 5^3 = 8 \times 125 = 1000 \)
Exercice 5
Calcule \( (10 / 2)^4 \).
Voir la correction
\( (10 / 2)^4 = 10^4 / 2^4 = 10000 / 16 = 625 \)










