Comment caractériser un son ? Pourquoi un son est-il fort ou faible, grave ou aigu ? Pourquoi peut-on faire la différence entre une voix et une flûte ? Tout ça, nous allons y répondre dans cette fiche sur les ondes sonores. Mais avant de te consacrer à ces ondes sonores, pour être au point sur les ondes mécaniques, fonce vite lire la fiche dédiée.
Intensité sonore et niveau sonore
Le son, ou onde sonore, est une onde mécanique progressive. Elle se propage donc dans un milieu matériel avec une certaine célérité et autres propriétés des la fiche dédiée.
Plus particulièrement, le son est une onde longitudinale qui va se propager par vibration des particules du milieu. Le son se propage comme une vague de compression sur un ressort.
OndesIntensité sonore
Il s’étend en 3 dimensions: Un émetteur crée autour de lui des vibrations sphériques qui vont se propager, comme des bulles qui deviennent de plus en plus grandes.
Le son qui se propage a une certaine intensité. Elle est notée \(I\) (en W/m²) et vaut
\(I = \dfrac{P}{S} \)
avec \(P\) la puissance du son (énergie par unité de temps, en W ou J/s) et \(S\) la surface de propagation du son (en m²).
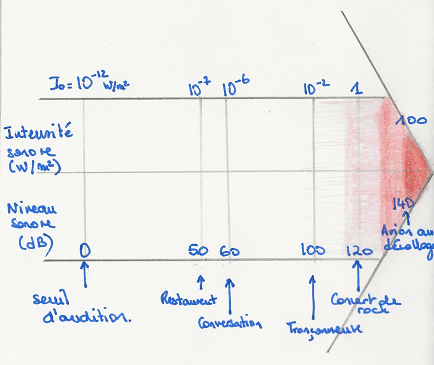
Dans la vie courante, on utilise la notion de niveau sonore, noté \(L\) (en décibels dB) qui est défini comme
\(L = 10\log(\dfrac{I}{I_{0}}) \)
avec \(I\), l’intensité sonore en W/m² et \(I_{0}\), l’intensité sonore de référence, qui vaut \(10^{-12}\) W/m².
Remarque
Le niveau sonore est croissant avec l’intensité sonore. Plus un son est fort plus son intensité et donc son niveau sonore sont grands.
\(I_{0}\) est l’intensité de référence. Le niveau sonore associé est de 0 dB. C’est le seuil d’audition.
Attention
Les intensités sonores s’additionnent, les niveaux sonores ne s’additionnent pas !
Les intensités sonores s’additionnent parce qu’elles dépendent directement de l’énergie, pas les niveaux sonores, qui eux ont une dépendance logarithmique !
Exemple
Si l’on avait le droit d’additionner les niveaux sonores, alors 2 personnes qui parlent en même temps (chacune à 60 dB) feraient le même bruit qu’un concert de rock (120 dB), c’est impossible !
Exercice
Deux personnes parlent en même temps, chacune à 60 dB. Quel est le niveau sonore total ? Combien de personnes doivent parler en même temps pour atteindre 120 dB (concert de rock) ?
Réponse
On ne peut pas additionner les niveaux sonores ! On additionne les intensités sonores, on calcule donc les intensités d’abord.
\(I_{1 personne} = I_{0}*10^{\frac{L}{10}} = 10^{-12}*10^{6} = 10 ^{-6}\) W/m²
Donc, \(I_{2 personnes} =2*I_{1 personne}= 2*10 ^{-6}\) W/m²
Ainsi, en appliquant la formule du niveau sonore, \(L_{2 personnes} = 10 \log(\frac{2*10 ^{-6}}{10^{-12}}) = 63\) dB.
Deux personnes parlant en même temps correspond à un niveau sonore de 63 dB, et pas 120 !
\(I_{concert} = 10^{-12} * 10^{120/10} = 1\) W/m²
\(N_{personnes} = \frac{I_{concert}}{I_{1 personne}} = \frac{1}{2*10^{-6}} = 0.5 * 10^6 = 500 000\) personnes
Pour arriver à 120 dB, il faut 500 000 personnes qui parlent en même temps.
C’est énorme et on voit bien deux choses:
- Les niveaux sonores ne s’additionnent pas
- Pour augmenter un petit peu le niveau sonore, il faut énormément faire augmenter l’intensité d’un son. C’est pour cela qu’il faut se méfier des sons trop forts, qui sont si intenses qu’il peuvent abîmer les oreilles.
Atténuation sonore
L’atténuation sonore, c’est la baisse du niveau sonore au cours de la propagation du son.
On peut la noter
\(A = L_{t} – L_{i} = 10 \log(\dfrac{I_{t}}{I_{i}}) \)
avec \(L_{i}\) et \(L_{t}\) les niveaux sonores de l’onde incidente (celle qui arrive, au départ) et de l’onde transmise (celle qui est propagée, à la fin), et \(I_{i}\) et \(I_{t}\) leurs intensités respectives.
Il y a deux sources notables d’atténuation: l’atténuation géométrique et l’atténuation par absorption.
1. Atténuation géométrique
L’atténuation géométrique est liée au fait que, lorsque que l’onde sonore se propage dans un milieu uniformément, elle évolue comme une bulle sphérique de vibrations qui grandit.
L’intensité du son vaut \(\frac{P}{S}\). Dans le cas d’une sphère, \(S = 4 \pi R^{2}\). Donc l’intensité du son peut s’écrire \(\frac{P}{4 \pi R^{2}}\), avec \({R}\) le rayon de la bulle de son. Lorsque le son se propage, la bulle grandit, donc R grandit, et I diminue.

En fait, la puissance du son doit se répartir sur plus de surface pour couvrir toute la sphère qui grandit. Il y a donc moins de puissance par unité de surface. Le son s’atténue.
2. Atténuation par absorption
L’atténuation par absorption est due à la perte d’énergie de l’onde sonore lorsqu’elle interagit avec les particules du milieu.
L’onde sonore se propage en faisant vibrer les particules les unes par rapport aux autres. Ces vibrations causent des frottements qui absorbent une partie de l’énergie du son: l’intensité sonore baisse.
Hauteur, timbre d’un son et analyse spectrale
On l’a vu, l’intensité sonore fait qu’un son est plus ou moins fort. Mais d’où vient la différence entre un son grave et un son aigu ?
1. Hauteur d’un son
Le son est une onde mécanique progressive dont la perturbation fait vibrer les particules du milieu. Cette vibration est un mouvement qui se fait avec une certaine fréquence. Cette fréquence est propre à ce son, c’est sa hauteur. Plus un son est haut (aigu), plus sa fréquence est grande.
Les fréquences audibles par l’homme se situent entre 20 Hz et 20 kHz. En-dessous de 20 Hz ce sont les infrasons, des sons si graves que l’on ne peut pas les entendre. Au-delà de 20 kHz, ce sont les ultrasons, des sons si aigus que l’on ne les entend pas.
Remarque
Ces valeurs ne sont que des approximations: l’oreille humaine évolue au cours du temps et en vieillissant on entendra de moins en moins les sons aigus.
2. Timbre d’un son
Le timbre d’un son, c’est la perception que l’on a de ce son. C’est parce que leur timbre est différent que l’on entend pas une voix de la même manière qu’une flûte.
Pour être plus clair, le timbre, c’est l’ensemble des fréquences qui sont contenues dans un son et leurs amplitudes.
Tout d’abord, il y a les sons purs. Ces ondes sonores sont parfaitement sinusoïdales (les particules du milieu vibrent de manière régulière). Le mouvement des particules peut être décrit par une unique fréquence, appelée le fondamental, noté \(f_{1}\).
Il y a ensuite les sons complexes. Le mouvement des particules n’est pas décrit par une seule fréquence, mais par plusieurs mouvements ayant chacun leur propre fréquence et leur propre amplitude.
Ainsi, un son complexe périodique se décompose en fonctions sinusoïdales de fréquence fondamentale \(f_{1}\), puis les fréquences \(f_{2} = 2 *f_{1}\), \(f_{3} = 3 *f_{1}\), etc. Les fréquences multiples du fondamental sont les harmoniques.
On peut représenter le timbre d’un son par son spectre. C’est un diagramme avec en x, la fréquence, et en y, l’amplitude (en dB). Ces diagrammes spectraux permettent de représenter visuellement le timbre d’un son et de voir en pratique les différences.
Exemples
Voici des spectres d’un \(La_{3}\) (440 Hz) qui est la note qui sert à accorder les instruments de musique. Ces spectres ont été obtenus, soit en jouant la note avec une flûte traversière, soit en chantant la note.
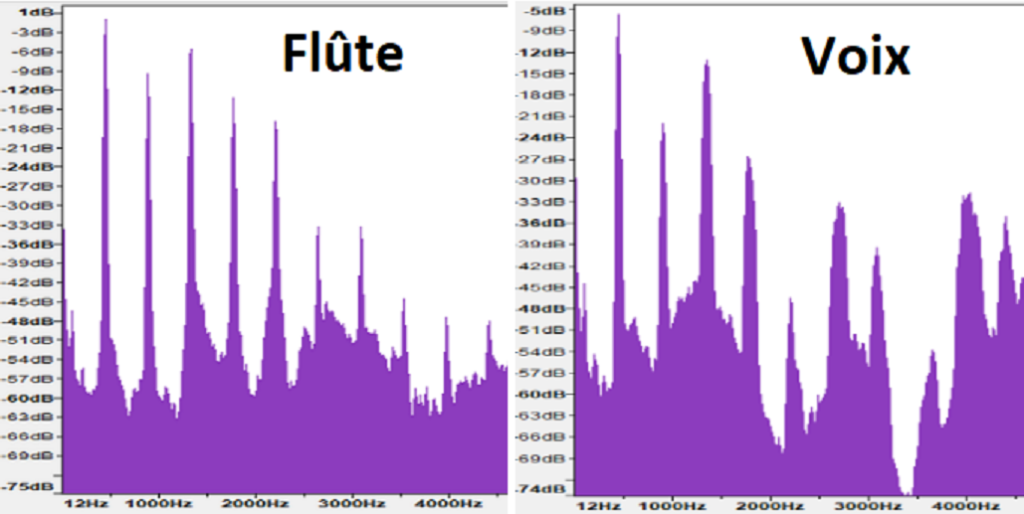
Si on ne fait attention qu’aux pics (le reste étant du bruit de fond), on remarque que plusieurs fréquences composent les spectres. Ce sont donc des sons complexes (sinon il n’y aurait qu’un seul pic, celui à la fréquence du son pur). Ces pics se trouvent aux fréquences multiples de 440Hz. On peut donc identifier le fondamental (440Hz) et ses harmoniques (880Hz, 1320Hz, etc.). Le son que l’on entend est celui de la fréquence du fondamental, on entend bien un \(La_{3}\).
Là où les spectres sont différents, c’est dans les amplitudes des pics. Ces différences d’amplitudes font que le timbre est différent, donc que l’on sait faire la différence entre une flûte qui joue et moi qui chante.
A retenir sur les ondes sonores
- Les ondes sonores sont des ondes mécaniques progressives longitudinales qui se propagent en 3 dimensions, par vibration des particules du milieu.
- L’intensité sonore vaut \(I = \frac{P}{S}\), en W/m², avec P la puissance du son (W), et S la surface sur laquelle il se propage (m²)
- Le niveau sonore associé vaut \(L = 10\log(\dfrac{I}{I_{0}})\) en dB, avec \(I_{0}\) l’intensité de référence, valant \(10^{-12}\) W/m²
- Inversement, \(I = I_{0} * 10^{\frac{L}{10}}\)
- Les intensités sonores s’ajoutent entre elles, pas les niveaux sonores !
- L’atténuation A (en dB) c’est la perte de niveau sonore d’un son qui se propage. Entre le son incident i et le son transmis t, \(A = L_{t} – L_{i} = 10 \log(\dfrac{I_{t}}{I_{i}})\)
- L’atténuation peut être géométrique (la surface de propagation grandit donc la puissance s’étale) ou par absorption (frottements des particules qui vibrent)
- Hauteur d’un son = Fréquence de ce son
- La plage de fréquences audibles va de 20Hz à 20kHz. En-dessous ce sont les infrasons graves, et au-dessus ce sont les ultrasons aigus
- Le timbre d’un son est l’ensemble des fréquences contenues dans un son et leurs amplitudes. On le représente graphiquement par un spectre (amplitude en fonction de la fréquence)
- Un son périodique a dans son spectre, une fréquence fondamentale (celle que l’on entend) et des harmoniques (multiples du fondamental)
Voilà qui conclut cet article sur la physique des ondes sonores. Découvre également notre fiche sur les trois lois de Newton !