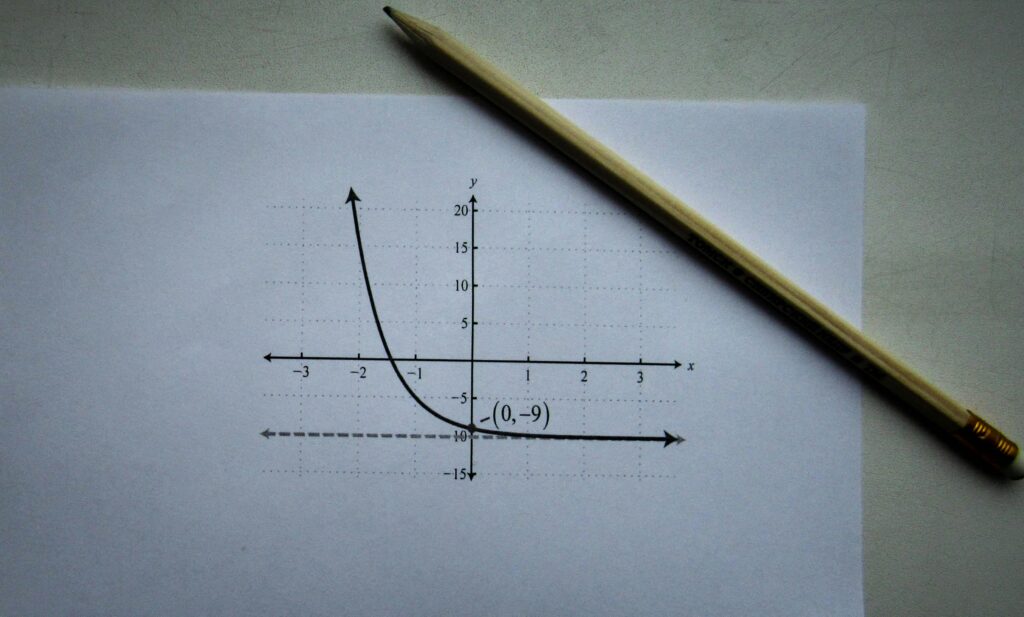
Les limites de fonctions : comprendre l’infini et les asymptotes

Les limites de fonctions sont un pilier fondamental de l’analyse mathématique. Elles permettent de modéliser le comportement d’une fonction lorsque la variable tend vers une valeur précise ou vers l’infini. Tu dois absolument comprendre les limites pour anticiper les variations, comprendre la notion de continuité, d’asymptotes et étudier en détail les points où le calcul « habituel » n’est plus possible sur une fonction. 

Définition de la limite en mathématiques

On dit que la fonction \( f \) admet pour limite le nombre \( L \) lorsque \( x \) tend vers une valeur \( a \) (finie ou infinie), si, pour toute valeur de \( x \) proche de \( a \), \( f(x) \) est aussi proche que l’on veut de \( L \).

En écriture académique : 

• Limite finie en a : \(  \lim_{x \to a} f(x) = L \)
• Limite infinie en a : \( \lim_{x \to a} f(x) = +\infty \text{ ou } -\infty \)

Les différents types de limites

Limite finie en un point

Lorsque la fonction approche une valeur réelle fixée près de a : 

• \(  \lim_{x \to 2} 3x + 1 = 7 \)

Limite infinie en un point

Quand la fonction « explose » et devient aussi grande (ou petite) que l’on veut :

• \(  \lim_{x \to 0^+} \frac{1}{x} = +\infty \)
• \(  \lim_{x \to 0^-} \frac{1}{x} = -\infty \)

Limite en l’infini

Décrit le comportement de f(x) lorsque x devient très grand ou très petit :

• \(  \lim_{x \to +\infty} \frac{2x + 3}{x – 1} = 2 \)
• \(  \lim_{x \to -\infty} x^2 = +\infty\)

Propriétés fondamentales des limites

• Linéarité : La limite d’une somme ou d’une différence est la somme ou la différence des limites (quand elles existent).
• Produit : Limite d’un produit = produit des limites.
• Quotient : Limite d’un quotient = quotient des limites, si la limite du dénominateur n’est pas 0.
• Composition : \(  \lim_{x \to a} f(g(x)) = f(\lim_{x \to a} g(x) \) si f est continue au point \( \lim_{x \to a} g(x) \)

💡 Remarque : en cas d’indétermination (ex : \( \frac{0}{0} \) ou \( \infty – \infty \)), il faut transformer la fonction pour lever l’ambiguïté.

Calcul de limites en mathématiques

Opérations sur les limites

Soulever une indétermination 

Les 4 formes indéterminées sont : 

• \( \infty – \infty \)
• \( \frac{\infty}{\infty} \)
• \( 0 \times \infty \)
• \( \frac{0}{0} \)

Factorisation par la monôme de plus haut degré

1. Identifier le terme de plus haut degré dans le numérateur et le dénominateur
2. Factoriser chaque terme par ce monôme dominant
3. Simplifier l’expression obtenue
4. Calculer la limite simplifiée

Multiplication par la forme conjuguée

1. Multiplier le numérateur et le dénominateur par l’expression conjuguée
2. Utiliser l’identité remarquable : \( (a − b)(a + b) = a^2 − b^2 \)
3. Simplifier et recalculer la limite

L’infini et les asymptotes

L’étude des limites infinies permet de mieux comprendre le comportement des fonctions lorsque les valeurs de x deviennent très grandes (ou très petites), ou lorsqu’une fonction « explose » à proximité d’un point donné. Cela conduit naturellement à la notion d’asymptote, qui décrit une direction vers laquelle la courbe d’une fonction tend sans jamais l’atteindre.

Asymptote horizontale 

Si \( \lim_{x \to +\infty} f(x) = L \), la droite d’équation \( y = L \) est appelée asymptote horizontale à la courbe de la fonction \( f \) en \( +\infty \)

Comment faire ? 

1. Calculer \( \lim_{x \to +\infty} f(x) \) et \( \lim_{x \to -\infty} f(x) \).
2. Si ces limites sont finies, alors l’équation de l’asymptote est : \( y = L \), où \( L \) est la valeur limite.

Asymptote verticale

Si \( \lim_{x \to A} f(x) = +\infty \) ou \( \lim_{x \to A} f(x) = -\infty \), la droite d’équation \(x = A \) est appelée asymptote verticale à la courbe de la fonction \( f \).

👉🏻 Comment faire ?

1. Identifier les valeurs interdites de \( f(x) \) (où le dénominateur s’annule ou où la fonction n’est pas définie).
2. Calculer \( \lim_{x \to a} f(x) \) en chaque valeur interdite \(a \).
3. Si \( \lim_{x \to a} f(x) = \pm\infty \), alors il y a une AV d’équation : \( x = a \)

Asymptote oblique

\( y = ax + b \) est une asymptote oblique à la courbe représentative de \( f \) en \( \infty \) si : \( \lim_{x \to \infty} \left( f(x) – (ax + b) \right) = 0 \).

Comment faire ? 

1. Vérifier les conditions préalables : la fonction doit tendre vers l’infini quand \( x \) tend vers l’infini
2. Déterminer le coefficient directeur \( a \) : calculer \( \lim_{x \to +\infty} \frac{f(x)}{x} \) ; Si cette limite existe et vaut \(a \) (avec \(a \neq 0 \)), alors la pente de l’asymptote est \(a \)
3. Déterminer l’ordonnée à l’origine \(b \) : calculer \( \lim_{x \to +\infty} [f(x) – ax] \); Si cette limite existe et vaut \( b \), alors l’ordonnée à l’origine est \( b\)
4. L’équation de l’asymptote oblique est \( y = ax + b \) ; On peut vérifier que \( \lim_{x \to +\infty} [f(x) – (ax + b)] = 0 \)

Théorèmes fondamentaux

Théorème des gendarmes

Soient trois fonctions \( f \), \( g \) et \( h \) définies sur un intervalle \( I \) et un réel \( a \) tel que :

• \( \forall x \in I$, $g(x) \leq f(x) \leq h(x) \)
• \( \lim\limits_{x \to a} g(x) = \lim\limits_{x \to a} h(x) = L \) 

Alors : \( \lim\limits_{x \to a} f(x) = L \)

Théorème de comparaison

\( \text{Soient } f, g : I \to \mathbb{R}, \text{ avec } a \in I, \text{ et } x \in I \setminus {a}. \text{Si } f(x) \leq g(x) \text{ pour tout } x \text{ proche de } a, \text{ et si } \lim_{x \to a} f(x) = \lim_{x \to a} g(x) = \ell, \text{ alors } \lim_{x \to a} h(x) = \ell \text{ pour toute fonction } h \text{ telle que } f(x) \leq h(x) \leq g(x). \)