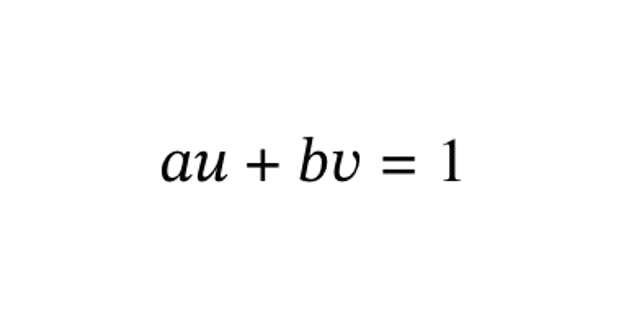Aujourd’hui, nous allons travailler ensemble sur une notion fondamentale en arithmétique : le théorème de Bézout ! Tu vas retrouver cette notion dans de nombreux concepts mathématiques, il est donc primordial de la comprendre et de savoir l’utiliser. Cet article est justement là pour te permettre de maîtriser toutes les propriétés et astuces autour du théorème de Bézout. Tu pourras même t’entraîner avec deux exercices corrigés à la fin de cet article !
Qu’est-ce que le théorème de Bézout ?
Le théorème de Bézout stipule que deux nombres \( a \) et \( b \) sont premiers entre eux si et seulement s’il existe deux entiers \( u \) et \( v \) tels que :
\[ \displaystyle au + bv = 1 \]
Pour rappel, un nombre premier est un nombre qui est divisible uniquement par 1 et par lui-même. Voici une liste des nombres premiers jusqu’à 100 que tu peux apprendre : \( 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, \)
\( 59, 61, 67, 71, 73, 79, 83, 89, 97 \)
Comme tu le sais, lorsque qu’en mathématiques, on utilise l’expression « si et seulement si », cela signifie que l’égalité ou l’équation marche dans les deux sens. Autrement dit, si tu prouves que \( au + bv = 1 \) alors les deux nombres \( a \) et \( b \) sont des nombres premiers. Inversement, si deux nombres \( a \) et \( b \) sont des nombres premiers alors on a \( au + bv = 1 \).
⚠️ Attention à ne pas faire d’erreur de rédaction dans tes calculs, surtout dans les matières scientifiques ! ⚠️
Ce théorème au programme de la spécialité mathématique est particulièrement utile pour identifier des nombres premiers, mais aussi pour trouver leur plus grand commun diviseur (PGCD) comme on le verra par la suite.
Un peu de culture sur le créateur du théorème de Bézout
Le théorème de Bézout est la généralisation du théorème formulé en 1624 par Claude-Gaspard Bachet dit de Méziriac. C’est le mathématicien Étienne Bézout (1730-1783) qui généralise ce théorème.
Étienne Bézout était un mathématicien français connu pour ses travaux sur la théorie des nombres ainsi qu’en algèbre. Il écrit de nombreux traités sur les équations algébriques, grâce auquel l’étude des déterminants s’améliore grandement au cours du XVIIIe siècle. Son théorème est un résultat fondamental en arithmétique modulaire et en théorie des nombres.
Lien entre le théorème de Bézout et le Plus Grand Commun Diviseur
On peut écrire à nouveau le théorème de Bézout à partir du Plus Grand Commun Diviseur de \( a \) et \( b\) tel que :
\[ \displaystyle au + bv = PGCD(a, b) \]
Pour rappel, le Plus Grand Commun Diviseur (PGCD) de deux nombres réels non nuls désigne le plus grand nombre entier possible qui divise ces deux nombres.
👉🏻 Tu as besoin d’un petit coup de pouce en mathématiques sur les racines carrées ou sur la fonction valeur absolue ? Jette un coup d’œil à nos articles sur tout ce qu’il faut savoir sur les racines carrées ou sur tout ce qu’il faut connaître sur la suite de Fibonacci et le nombre d’or 👈🏻
Par exemple, le PGCD de 12 et 24 est 12, car les diviseurs de 12 sont :
- \( 1, 2, 3, 4, 6, 12 \)
Et de 24 :
- \( 1, 2, 3, 4, 6, 8, 12, 24 \)
Par ailleurs, cette nouvelle écriture du théorème de Bézout est fondamentale ! C’est elle qui va nous permettre de montrer s’il existe réellement des solutions \( u \) et \( v \) possibles pour pouvoir ensuite les trouver. En effet, l’équation \( \displaystyle au+bv = c \) admet des solutions entières si et seulement si le PGCD(a,b) divise \( c \).
Comment trouver le PGCD en mathématiques ?
Pour trouver le PGCD de deux nombres, plusieurs méthodes sont envisageables.
La liste des diviseurs
Tout d’abord, tu peux lister tous les diviseurs de ces deux nombres. Cette méthode est la plus fastidieuse surtout lorsque les nombres sont grands, mais elle est aussi la plus simple. Ainsi, pour trouver le PGCD de 12 et 18. On peut écrire tous leurs diviseurs :
- les diviseurs de 12 : \( 1, 2, 3, 4, 6, 12 \)
- les diviseurs de 18 : \( 1, 2, 3, 4, 6, 9, 18 \)
On a donc \( \displaystyle \text{PGCD}(12, 18) = 6 \)
L’algorithme d’Euclide
Une autre méthode possible est celle utilisant l’algorithme d’Euclide. Parmi les deux nombres à diviser tu vas identifier le plus grand et le plus petit.
Cette méthode consiste alors à diviser le plus grand nombre par le plus petit. Tu vas alors trouver un reste. Puis tu vas diviser alors le plus petit nombre par ce reste. Il faut alors répéter ces séries d’opérations jusqu’à obtenir un reste nul.
Ainsi pour trouver le PGCD de 12 et 18, on commence par diviser 18 par 12 et on obtient alors :
\[ \displaystyle 18 = 1 \times 12 + 6 \]
Le reste est donc 6. On divise alors 12 par 6 et on obtient :
\[ \displaystyle 12 = 1 \times 6 + 0 \]
Le reste est nul. Donc le PGCD de 12 et 18 est 6.
Cette méthode est la plus rapide, notamment lorsque les deux nombres initiaux sont très grands.
La décomposition en produits de nombres premiers
La dernière méthode consiste à développer chaque nombre initial en produit de nombres premiers les plus petits possibles pour identifier les nombres en commun. Il faut alors choisir les nombres premiers communs avec les plus petits exposants. Prenons un exemple, pour mieux comprendre cette méthode !
Ainsi, on a :
\[
12 = 2^2 \times 3
\]
\[
18 = 2 \times 3^2
\]
Ici, on constate que les facteurs premiers avec les plus petits exposants sont 3 dans la première équation et 2 dans la seconde. Le PGCD de 12 et 18 est donc le produit de ces deux nombres. Ainsi, on a :
\[ \displaystyle
\text{PGCD}(12,18) = 2^{1} \times 3^{1} = 2 \times 3 = 6
\]
Exercices d’entraînement sur le théorème de Bézout
Exercice 1
En utilisant la définition du théorème de Bézout et ses différentes caractéristiques. Trouve deux entiers u et v tels que :
\[ \displaystyle 15 \times u + 6 \times v = 30 \]
Exercice 2
En utilisant le théorème de Bézout, montre que les entiers 7 et 5 sont premiers entre eux.
Corrigés des exercices sur le théorème de Bézout
Corrigé de l’exercice 1
On commence par vérifier si des solutions entières existent grâce à la reformulation du théorème de Bézout avec le PGCD. Or les diviseurs de 15 sont \( 1, 3, 5, 15 \) et les diviseurs de 6 sont \( 1, 2, 3, 6 \)
Ainsi, on constate que le Plus Grand Commun Diviseur de 15 et 6 est 3. On a donc \( \displaystyle \text{PGCD}(15, 6) = 3 \)
Or 30 est bien divisible par 3. Il existe donc des solutions \( u \) et \( v \) entières.
Pour trouver les solutions \( u \) et \( v \), le plus simple est de commencer par essayer avec des valeurs simples dans ta tête, comme \( 0, 1, -1, 2 \) ou encore \( -2 \).
Or ici une solution apparaît assez rapidement puisque qu’avec \( v = 0 \) on a alors \( 15u = 30 \) donc \( u = 2 \). Inversement on aurait pu choisir \( u = 0 \) on a alors \( 6v = 30 \) donc \( v = 5 \).
Deux réponses possibles sont donc (2;0) et (0;5) mais il en existe une infinité.
Corrigé de l’exercice 2
Pour montrer que 7 et 5 sont premiers entre eux, en utilisant le théorème de Bézout. Il faut donc trouver \( u \) et \( v \) tel que
\[ \displaystyle 7u + 5v = 1 \]
Pour trouver \( u \) et \( v \), le plus simple est de s’intéresser au PGCD de ces deux nombres. Or en réduisant avec le plus petit produit possible, on constate que :
\[ \displaystyle 7= 1 \times 5+ 2 \]
\[ \displaystyle 5 = 2 \times 2+1 \]
\[ \displaystyle 2 = 2 \times 1 + 0 \]
Le plus grand commun diviseur (PGCD) de 7 et 5 est donc 1. Ces deux nombres sont donc des nombres premiers. Mais on va aller encore plus loin, en identifiant \( u \) et \( v \) grâce à cette décomposition.
En effet, on a d’après la première décomposition, \( \displaystyle 2 =7 − 1 \times 5 \). On remplace alors dans l’équation recherchée, autrement dit \( \displaystyle 7u + 5v = 1 \) et on trouve :
\[ \displaystyle
1 = 5 – 2 \times (7 – 1 \times 5)
\]
\[ \displaystyle
1 = 5 – 2 \times 7 + 2 \times 5
\]
\[ \displaystyle
1 = (3 \times 5) – (2 \times 7)
\]
\[ \displaystyle
1 = (-2) \times 7 + 3 \times 5
\]
On trouve donc que \( u = -2 \) et \( v = 3 \). Mais en réalité, il existe une infinité de réponses possibles.
Ce que tu dois retenir sur le théorème de Bézout
Voilà, tu connais maintenant tout sur le théorème de Bézout ! Tu es désormais capable d’énoncer sa définition ainsi que ses différentes propriétés. Tu t’es même entraîné avec deux exercices sur cette notion fondamentale ! J’espère que cet article t’a plu. Tu peux retrouver ici toutes nos autres ressources mathématiques et lire cet article sur les techniques de conversion des unités de longueur !