Le chapitre sur les complexes est un bloc important du programme de terminale S et il est impossible de réussir un exercice sans savoir utiliser le cercle trigonométrique ! Up2School a donc décidé de vous rédiger cet article pour revoir ensemble tout ce qu’il y a à savoir. Le cercle trigonométrique permet notamment de déterminer l’argument d’un nombre complexe.
🤓 Si jamais tu as des doutes sur la notion d’argument ou sur les nombres complexes en général, n’hésite pas à relire notre article disponible à ce sujet.
Le cercle trigonométrique, qu’est-ce que c’est ?
Qu’est-ce qu’un cercle trigonométrique ? Il s’agit d’un cercle centré en 0 et de rayon 1. On trace souvent ce cercle dans le plan complexe, c’est-à-dire que l’axe des ordonnées correspond à la partie imaginaire et l’axe des abscisses correspond à la partie réelle. Ainsi, le nombre \(z=2+4i\) sera représenté sur ce graphique par le point d’abscisse 2 et d’ordonnée 4 ! Il est important de comprendre le sens de lecture du texte, qui se fait dans le sens des aiguilles d’une montre.
On parle de cercle trigonométrique, car on vient placer des angles sur le cercle !
Comment construire un cercle trigonométrique ? Méthode étape par étape
Il est primordial de savoir tracer rapidement un cercle trigonométrique sur un brouillon.
Étape préliminaire : savoir lire le cercle trigonométrique
Pour le construire, il faut comprendre le lien entre ce cercle et le sinus / le cosinus d’un angle. Considérons un point M sur le cercle, on forme ainsi un angle \( \alpha\) avec l’axe des abscisses. Maintenant, en revenant à la définition du cosinus et du sinus, on remarque qu’on retrouve ces valeurs sur le schéma suivant :
On remarque donc sur cette figure qu’on peut :
- Lire le cosinus sur l’axe des abscisses
- Lire le sinus sur l’axe des ordonnées
C’est grâce à cela que l’on va construire le cercle.
Étape 1 – Tracer l’axe des ordonnées et des abscisses et le cercle
On commence par tracer l’axe des ordonnées et des abscisses, puis on dessine un cercle que l’on essaie de centrer au niveau de l’origine.
Étape 2 – Placer les angles
On continue en plaçant les angles très simples, à savoir \(0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}\). Ces angles doivent être appris par cœur et doivent constituer une référence incontournable du cercle trigonométrique dans ton esprit.
On obtient la figure suivante :
Étape 3 – Tracer les bissectrices
On trace ensuite les bissectrices (en rouge)
Étape 4 – Tracer les lignes supplémentaires
Tracer les lignes supplémentaires (en noir) pour que le cercle ressemble finalement à ça :
On peut s’aider des lignes en pointillé, mais elles restent optionnelles et non obligatoires
Étape 5 – Placer les angles
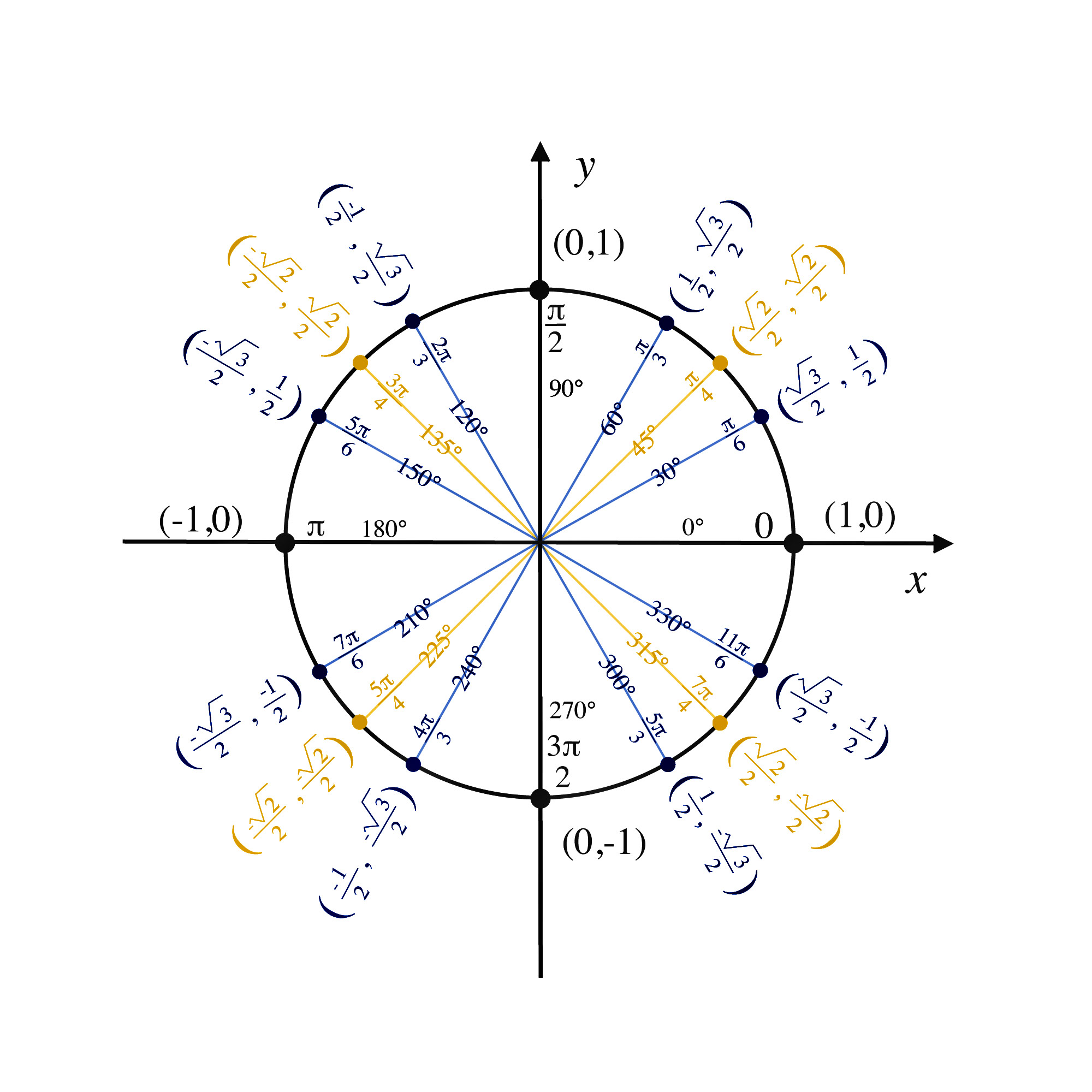
Placer et apprendre les angles du cercle trigonométrique dans le côté du cercle qui se situe en haut à droite. Il est indispensable de connaître ces 5 angles par cœur (\(0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}\)), car à partir de ceux-là, tu pourras ensuite retrouver tous les autres angles du cercle trigonométrique.
Enfin, on complète en utilisant les valeurs connues de sinus et cosinus qu’on vous rappelle ici :
\(\begin{array}{|l|c|c|c|c|c|c|c|c|c|}
\hline \boldsymbol{x} \text { (en rad) } & 0 & \frac{\pi}{6} & \frac{\pi}{4} & \frac{\pi}{3} & \frac{\pi}{2} & \frac{2 \pi}{3} & \frac{3 \pi}{4} & \frac{5 \pi}{6} & \pi \\
\hline \sin x & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 \\
\hline \cos x & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 & -\frac{1}{2} & -\frac{\sqrt{2}}{2} & -\frac{\sqrt{3}}{2} & -1 \\
\hline
\end{array}\)
On remarque que pour ces angles, il y a toujours une valeur, soit le cosinus soit le sinus qui est facile à placer sur l’axe correspond. Par exemple, pour \(\frac{\pi}{6}\) le sinus vaut un demi. On peut donc placer ce point puis tracer la droite parallèle à l’axe des abscisses passant par ce point, l’intersection de cette droite avec le cercle permet de placer le point. Voici ce que cela donne :
En faisant cela pour toutes les valeurs, on obtient le cercle trigonométrique complet !
Quel lien entre le cercle trigonométrique et les nombres complexes ?
Regarde cette vidéo avant de commencer, qui t’expliquera les formes trigonométriques (le cercle trigonométrique) et le lien avec les nombres complexes !
On a donc construit un cercle trigonométrique, mais à quoi cela sert-il ? Il sert principalement pour trouver l’argument d’un nombre complexe.
Pour rappel l’argument d’un complexe c’est l’angle qu’il forme avec l’axe des abscisses, qui est représenté par theta sur la figure suivante :
Considérons le nombre complexe, écrit sous forme algébrique \(z=2+2i\).
Il faut ensuite le mettre sous forme trigonométrique ou exponentielle. On peut déterminer le module puis l’argument.
On a \(|z|=\sqrt{2^2+2^2}= \sqrt{8} = 2 \sqrt{2}\)
Pour trouver l’argument on peut utiliser plusieurs techniques :
- On factorise par le module. Ce qui donne \(z= 2\sqrt{2}(\frac{1}{\sqrt{2}}+ i \frac{1}{\sqrt{2}})\). On cherche alors un angle tel que \(\cos(\theta) = \frac{\sqrt{2}}{2}\) et \(\sin(\theta) = \frac{\sqrt{2}}{2}\). Le tableau ou le cercle nous permettent de trouver \(\theta= \frac{\pi}{4}\).
- Ensuite, on utilise la formule avec l’arctangente. $$\theta = arctan(\frac{2}{2})= \arctan(1) = \frac{\pi}{4}$$
- on trace le cercle trigonométrique, on place le point et on lit l’angle (cette méthode permet de trouver graphiquement l’angle mais ne justifie pas la réponse ! )
On obtient donc l’écriture trigonométrique suivante : $$ z=2 \sqrt{2}(\cos(\frac{\pi}{4})+ i \sin(\frac{\pi}{4}))$$
Et l’écriture exponentielle :
$$z=2 \sqrt{2} e^{i \frac{\pi}{4}}$$
La trigonométrie expliquée dans une vidéo très complète
Si des paroles valent plus que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette vidéo explicative de Ambroise réalisée sur notre chaîne YouTube, il détaille vraiment tout ce que tu dois connaître de la trigonométrie dans les moindres détails…
Prendre de l’avance sur le programme de terminale (en prépa ECG !)
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes les ressources associées à la trigonométrie :
Voilà qui conclut cette fiche sur le cercle trigonométrique. D’ailleurs, n’hésite pas à t’entraîner sur nos annales de bac !
FAQ sur le cercle trigonométrique
Qu’est-ce qu’un cercle trigonométrique ?
Le cercle trigonométrique est un cercle de rayon 1 centré sur l’origine d’un repère orthonormé. Il est utilisé en trigonométrie pour définir les angles et les valeurs des fonctions trigonométriques (sinus, cosinus, tangente).
À quoi sert le cercle trigonométrique ?
Il permet de représenter visuellement les angles en radians, de déterminer les valeurs des fonctions trigonométriques et d’étudier les propriétés des angles remarquables (30°, 45°, 60°…).
Pourquoi utilise-t-on les radians sur le cercle trigonométrique ?
Les radians sont une unité naturelle de mesure des angles qui facilitent les calculs. Un tour complet du cercle correspond à 2π radians, ce qui simplifie les formules trigonométriques.
Comment trouver les valeurs du sinus et du cosinus sur le cercle trigonométrique ?
Pour un angle donné, la valeur du cosinus correspond à l’abscisse du point sur le cercle, et la valeur du sinus à son ordonnée.
Quelles sont les coordonnées des points remarquables sur le cercle trigonométrique ?
Les points remarquables sont : (1,0) pour 0 rad, (0,1) pour π/2 rad, (-1,0) pour π rad et (0,-1) pour 3π/2 rad.
Comment utiliser le cercle trigonométrique pour résoudre une équation trigonométrique ?
Pour résoudre une équation comme cos(x) = 1/2, on repère sur le cercle les angles où le cosinus vaut 1/2 : π/3 et -π/3. On généralise avec la périodicité des fonctions trigonométriques.
