La loi de Beer-Lambert est une des pierres angulaires de la spectrophotométrie, technique largement utilisée en physique-chimie et dans de nombreux domaines scientifiques pour quantifier la concentration d’une substance en solution. Que ce soit en laboratoire, dans le contrôle qualité industriel ou dans l’environnement, cette loi permet de relier de façon simple et directe une grandeur optique mesurable, l’absorbance, à la concentration chimique. Cet article détaillé s’appuie sur des démonstrations accessibles, des conditions d’application, ainsi que des exemples et exercices pour renforcer ta compréhension.
Introduction générale : de quoi parle-t-on ?
Quand un rayon lumineux traverse une solution colorée, son intensité diminue. Cette diminution provient de l’absorption de photons par les molécules présentes dans la solution. Plus une solution est concentrée, plus l’intensité sera atténuée. La loi de Beer-Lambert formalise et quantifie précisément cette diminution en relation à la concentration.
Pour la mesurer, on utilise un spectrophotomètre qui compare l’intensité lumineuse avant et après passage à travers la solution, afin d’évaluer la proportion de lumière absorbée.
Définitions des grandeurs physiques
- Intensité incidente : Puissance lumineuse entrant dans la solution à la longueur d’onde considérée.
- Intensité transmise : Puissance lumineuse sortant de la solution.
- Transmittance : Fraction de lumière transmise, définie par :
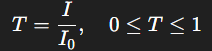
- Absorbance : Grandeur sans dimension donnée par :
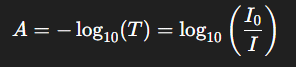
Énoncé de la loi de Beer-Lambert
La loi s’exprime par la relation : A=ε×ℓ×c
Où :
- A : Absorbance (sans unité)
- ε : Coefficient d’extinction molaire de l’espèce chimique à la longueur d’onde donnée (en L·mol⁻¹·cm⁻¹)
- ℓ : Longueur de la cuve, c’est-à-dire la distance parcourue par la lumière dans la solution (en cm)
- c : Concentration de la substance absorbante (en mol·L⁻¹)
Cette relation montre que l’absorbance est proportionnelle à la concentration, ce qui permet de calculer c si ε et ℓ sont connus.
Interprétation physique et mathématique
Considérons un faisceau lumineux monochromatique traversant une solution.
La diminution d’intensité lumineuse sur une épaisseur infinitésimale dx est proportionnelle à l’intensité courante I et au nombre de molécules absorbantes rencontrées sur dx, soit :
dI = -κ I dx
Avec κ un coefficient d’absorption linéaire. Par intégration entre 0 et ℓ, on obtient :
I = I₀ e^(-κ ℓ)
La transmittance s’écrit ainsi :
T = I / I₀ = e^(-κ ℓ)
Prenant le logarithme décimal, on obtient l’absorbance :
A = -log₁₀(T) = log₁₀(I₀ / I)
La proportionnalité entre A et κ ℓ découle du changement de base du logarithme.
Or, κ est proportionnel au nombre de particules absorbantes par unité de volume, ce qui est directement lié à la concentration c (mol·L⁻¹). Ainsi, on peut écrire :
A = ε ℓ c
Où ε est une constante spécifique à chaque molécule et à la longueur d’onde.
Conditions et limites d’application
La loi est simple mais ne s’applique correctement que sous certaines conditions, qui sont à connaître absolument :
- Lumière monochromatique ou quasi-monochromatique à une longueur d’onde précise, généralement le pic maximal d’absorption.
- Solutions diluées et limpides : éviter la diffusion de la lumière par des particules en suspension.
- Absorbance dans une gamme raisonnable, typiquement <1,5 à 2 ; au-delà, la relation linéaire se dégrade.
- Comportement non interférent entre molécules : pas d’associations, de complexes ou d’interactions modifiant l’absorption.
Au-delà, des corrections sont à appliquer ou la loi doit être remplacée par des modélisations plus complexes.
Applications pratiques
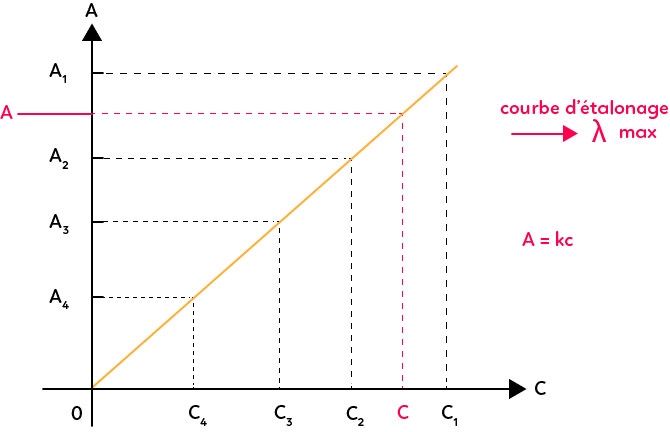
Dosage d’une espèce inconnue par étalonnage
L’utilisation la plus classique : doser une solution.
- Étape 1 : Préparer une gamme d’étalons de concentrations connues.
- Étape 2 : Mesurer l’absorbance A de chaque étalon.
- Étape 3 : Tracer A = f(c), vérifier que c’est une droite passant par l’origine.
- Étape 4 : Mesurer l’absorbance Aₓ de la solution inconnue.
- Étape 5 : Lire la concentration cₓ correspondante sur la droite (ou utiliser la formule).
Analyse de mélanges
Lorsque différentes espèces absorbent à différentes longueurs d’onde, on mesure les absorbances aux longueurs d’onde spécifiques de chaque composé. La relation additive :
Aₜₒₜₐₗ(λ) = ∑ᵢ εᵢ(λ) ℓ cᵢ
Permet de calculer chacune des concentrations en résolvant un système d’équations.
Exemple détaillé
On mesure le dosage du permanganate de potassium (KMnO₄) en milieu aqueux. À λₘₐₓ = 525 nm, le coefficient d’extinction molaire est ε = 2250 L·mol⁻¹·cm⁻¹, avec une cuve de 1 cm.
Absorbance mesurée de la solution :
A = 0.90
Calcul de la concentration c :
c = A / (ε ℓ) = 0.90 / (2250 × 1) = 4.0 × 10⁻⁴ mol·L⁻¹Équipements et montage expérimental
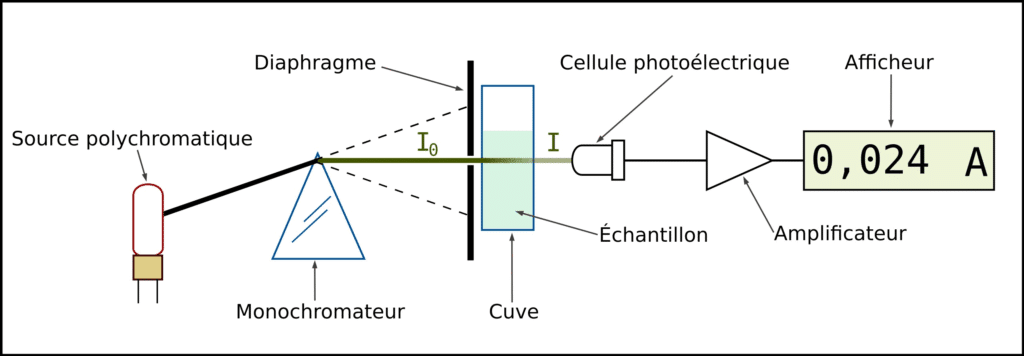
Un spectrophotomètre se compose de :
- Source lumineuse (lampe à deutérium, tungstène, etc.)
- Monochromateur (prisme ou réseau) pour sélectionner la λ
- Cuvette contenant la solution
- Détecteur mesurant I et I₀
- Unité de calcul affichant l’absorbance
Afin que les expériences aboutissent, il faut toujours :
- Utiliser toujours une cuve propre et d’épaisseur connue.
- Éviter la présence de bulles ou de particules dans la solution.
- Faire un « blanc » en mesurant la solution sans la substance absorbante (solvant seul).
- Vérifier la linéarité de la courbe d’étalonnage avant toute mesure.
Teste tes connaissances !
Questions :
- Quelle grandeur mesure directement un spectrophotomètre ?
- Que représente le coefficient ε dans la loi de Beer-Lambert ?
- Comment varie l’absorbance si on double la concentration ?
- Que fait l’absorbance si on quadruple la longueur de la cuve ?
- Pourquoi faut-il choisir une longueur d’onde d’absorption maximale ?
- À quoi correspond une absorbance A=0 ?
- Quel est l’effet de l’augmentation de la longueur d’onde sur l’absorbance ?
- Comment varie la transmittance lorsqu’on augmente la concentration ?
- Que se passe-t-il pour l’absorbance si la solution est trop concentrée ?
- Quelle est l’unité de la concentration dans l’expression de la loi de Beer-Lambert ?
Réponses :
- L’absorbance
- Le coefficient d’extinction molaire de l’espèce chimique
- Elle double (proportionnelle)
- Elle quadruple (proportionnelle)
- Pour maximiser la sensibilité et la précision des mesures
- Aucune lumière n’est absorbée (transmission totale)
- L’absorbance augmente généralement (jusqu’à une certaine limite)
- La transmittance diminue
- L’absorbance peut devenir trop élevée et dépasser la gamme linéaire du spectrophotomètre
- mol·L⁻¹
Pour aller plus loin, je te conseille vivement de visionner ces deux vidéos :
Conclusion
La loi de Beer-Lambert est un outil indispensable pour toute analyse quantitative par absorption lumineuse. Sa simplicité, sa robustesse et sa généralité permettent d’aborder des mesures fiables de concentration dans des domaines très variés, du contrôle médical à la chimie industrielle. Comprendre cette loi, ses hypothèses et applications vous donnera toutes les clés pour exploiter pleinement la spectrophotométrie, que ce soit lors des examens du bac, en travaux pratiques ou dans la recherche scientifique par la suite.