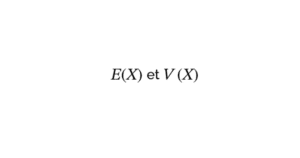Si tu es actuellement en terminale complémentaire, tu as sûrement déjà entendu parler des lois exponentielles. Si tu n’as pas compris ce chapitre ou si tu veux approfondir cette notion pour le baccalauréat, cet article est fait pour toi.
Comment définir une loi exponentielle ?
Soit \( \lambda \) un réel strictement supérieur à 0.
On dit qu’une variable aléatoire suit une loi exponentielle de paramètre \(\ \lambda \) lorsque \(\ f(x) = \begin{cases} \lambda*e^{-\lambda(x)} &\text{si} \; x ≥ 0\\ 0 &\text{si} \; x < 0 \end{cases} \)
Soit \(\ X \) une variable aléatoire qui suit une loi exponentielle de paramètre \( \lambda \).
La fonction de répartition de \(\ X \) sur \(\ R \) est définie par :
\(\ F(x) = \begin{cases} 1- e^{-\lambda(x)} &\text{si} \; x ≥ 0\\ 0 &\text{si} \; x < 0 \end{cases} \)
L’espérance d’une variable aléatoire \(\ X \) qui suit une loi exponentielle de paramètre \(\ \lambda \) est \(\ E(X) = \frac{1}{\lambda} \).
Calculer une probabilité avec une loi exponentielle
À toi de jouer :
Soit \(\ X \) une variable aléatoire qui suit une loi exponentielle de paramètre \(\ \lambda = 2 \)
- Calcule (1) \(\ P(X≤3) \), (2) \(\ P(X≥2) \) et (3) \(\ P(2<X<3) \).
Rappel :
Soit \(\ X \) une variable aléatoire de densité \(\ f \).
On note \(\ F \) la fonction de répartition de la variable aléatoire \(\ X \) définie par tout réel \(\ x \) par \(\ F(x) = P(X≤x) \).
On peut aussi rappeler que pour tous réels \(\ a \) et \(\ b \) avec \(\ a≤b \), on a :
-
\(\ P(a≤X≤b) = P(a<X≤b) = P(a≤X<b) = P(a<X<b) = F(b) – F(a) \), avec \(\ F \) la fonction de répartition de X.
-
\(\ P(X≥a) = 1-P(X≤a) = 1-F(a) \), avec \(\ F \) la fonction de répartition de \(\ X \).
(1) Ainsi, \(\ P(X≤3) = F(3) = 1-e^{-3*2}= 1-e^{-6} \).
(2) De même, \(\ P(X≥2) = 1-P(X≤2) = 1-(1- e^{-2*2}) = e^{-4} \).
(3) Ensuite, \(\ P(2<X<3)= P(2≤X<3) = P(2<X≤3) = P(2≤X≤3)=F(3) -F(2) = 1-e^{-6} – (1-e^{-4})=1-e^{-6}-1+e^{-4} = e^{-4}-e^{-6} \).
Résoudre un problème à l’aide de la loi exponentielle
Dans cet exercice, on étudie une variable aléatoire X égale au temps d’attente d’un usager à un arrêt de bus.
On considère que \(\ X \) suit une loi exponentielle de paramètre 0,1.
(1) Quelle est la durée moyenne d’attente pour prendre le bus ?
(2) Montrer que la probabilité pour que l’usager attende entre 5 et 15 minutes est d’environ 0,38.
(3) Calculer la probabilité que l’usager attende moins de 5 minutes.
(4) Calculer la probabilité que l’usager attende plus de 15 minutes.
(1) Pour calculer le temps d’attente moyen, il faut utiliser l’espérance.
Ainsi \(\ E(X) = \frac{1}{\lambda} = \frac{1}{0,1} = 10 \), car la variable aléatoire \(\ X \) suit une loi exponentielle de paramètre \(\ \lambda = 0,1 \).
L’usager attendra en moyenne 10 minutes.
(2) Pour calculer la probabilité que l’usager attende entre 5 et 15 minutes, il faut utiliser cette propriété \(\ P(a≤X≤b) = P(a<X≤b) = P(a≤X<b) = P(a<X<b) = F(b) – F(a) \), avec \(\ F \) la fonction de répartition de \(\ X \).
Dans cette exemple \(\ a = 5 \) et \(\ b = 15 \), on a donc bien \(\ a ≤ b \) autrement dit \(\ 5 ≤ 15\).
Ainsi, \(\ P(5≤X≤15) =F(15) – F(5) = 1-e^{-15*0,1}-(1-e^{-5*0,1}) = e^{-0,5}-e^{-1,5} ≈ 0,38 \).
La probabilité que l’usager attende entre 5 et 15 minutes est d’environ 0,38.
(3) Pour calculer la probabilité que l’usager attende plus de 15 minutes, il faut utiliser cette propriété : \(\ P(X≥a) = 1-P(X≤a) = 1-F(a) \), avec \(\ F \) la fonction de répartition de \(\ X \).
Dans cette exemple \(\ a = 15 \), ainsi \(\ P(X≥15) = 1-P(X≤15) = 1-F(5) = 1-(1-e^{-15*0,1}) = e^{-1,5} ≈ 0,22\).
La probabilité pour que l’usager attende plus de 15 minutes est d’environ 0,22.
(4) Pour calculer la probabilité que l’usager attende moins de 5 minutes, on peut utiliser deux méthodes.
i) On peut utiliser la définition de la fonction de répartition de \(\ X \) que tu es habitué à utiliser, c’est-à-dire : \(\ P(X≤5) = F(5) = 1-e^{-0,1*5}=1-e^{-0,5} \).
ii) On peut utiliser le fait que \(\ \int_{-∞}^{+∞}f(t)dt=1\).
Rappel :
Soit \(\ X \) une variable aléatoire continue. On sait que \(\ X \) suit une loi de probabilité de densité \(\ f \) lorsqu’il existe une fonction \(\ f \) continue, positive sur un intervalle \(\ I \) de \(\ R \) telle que :
- Si \(\ I ∈ [a ;b] \),\(\ \int_{a}^{b}f(t)dt=1\).
- Et plus généralement, si \(\ I ∈ R \), \(\ \int_{-∞}^{+∞}f(t)dt=1\). .
On sait également que, \(\ \int_{-∞}^{+∞}f(t)dt= \lim \limits_{x \to – \infty} \int_{x}^{a}f(t)dt + \int_{a}^{b}f(t)dt +\lim \limits_{x \to +\infty} \int_{b}^{x}f(t)dt \), d’après Chasles.
Or, on sait d’après notre cours que pour tout réel \(\ a \), on a : \(\ F(a)=P(X≤a)= \lim \limits_{x \to – \infty} \int_{x}^{a}f(t)dt \) et pour tout réel \(\ b \), \(\ F(b)=P(X≥b)= \lim \limits_{x \to +\infty} \int_{b}^{x}f(t)dt \).
Et pour tout réel \(\ a \) et \(\ b \) tels que \(\ a ≤ b \), on a : \(\ F(b)-F(a)= F(a≤X≤b) = \int_{a}^{b}f(t)dt \).
Alors, \(\ \int_{-∞}^{+∞}f(t)dt= \lim \limits_{x \to – \infty} \int_{x}^{a}f(t)dt + \int_{a}^{b}f(t)dt +\lim \limits_{x \to +\infty} \int_{b}^{x}f(t)dt =P(X≤a)+P(a≤X≤b)+P(X≥b) \).
Ainsi, dans notre exemple, si on remplace \(\ a \) par 5 et \(\ b \) par 15, avec l’intervalle \(\ [0 ; +∞[ \), on obtient donc pour tout \(\ x ≥0 \), \(\ \lim \limits_{x \to +\infty} \int_{0}^{x}f(t)dt \).
Or, \(\ \lim \limits_{x \to +\infty} \int_{0}^{x}f(t)dt =P(X≤5)+P(5≤X≤15)+P(X≥15) =1 \).
Donc \(\ P(X≤5)= 1-P(X≥15) – P(5≤X≤15)= 1- e^{-1,5} –( e^{-0,5}-e^{-1,5})= 1-e^{-0,5}≈0,39\).
La probabilité pour que l’usager attende moins de 5 minutes est d’environ 0,39.
Dans cet exemple, il est préférable d’utiliser la première méthode, mais dans des cas plus complexes, il est envisageable d’utiliser la seconde.
Lire aussi : Tout comprendre aux sommes
Pour aller plus loin
Si la variable aléatoire \(\ X \) suit une loi exponentielle de paramètre \(\ \lambda >0 \) alors :
X admet une variance : \(\ V(X) = \frac{1}{\lambda} \).
Soit \(\ X\) une variable aléatoire qui suit une loi exponentielle de paramètre \(\ \lambda >0 \).
Pour tout réel t et s strictement supérieurs à 0, on sait que :
\(\ P_{(X>t)} (X>t+s)=P(X>s) \).
À toi de jouer :
Reprenons le problème, imaginons que des usagers attendent le bus depuis 10 minutes bus, calcule le temps d’attente qu’ils l’attendent 5 minutes de plus.
D’après la propriété d’absence de mémoire pour les lois exponentielles, on a \(\ P_{(X>10)} (X>10+5)=P(X>5)=1-(1-e^{-0,1*5})= e^{-0,5} \).
Lire aussi : Les méthodes pour étudier le sens de variation d’une suite