Si tu cherches à mieux comprendre les matrices et les systèmes d’équations, cet article est fait pour toi ! Ces outils sont partout en mathématiques, que ce soit en algèbre, en géométrie ou même en sciences appliquées. Que tu sois en train de préparer ton bac ou simplement curieux de mieux gérer les exercices de lycée, maîtriser ces notions peut vraiment t’aider à gagner en confiance et en efficacité. Dans cet article, je vais t’expliquer tout ça de façon claire et simple, histoire que tu puisses enfin dompter ces concepts sans prise de tête !
Rappels de définitions des matrices et des systèmes d’équations et explication de leur lien
1.1 Définitions fondamentales des matrices et des systèmes d’équations
Imagine un tableau de points dans un jeu vidéo où chaque case peut contenir un nombre : tu obtiens une matrice ! C’est un objet clé des maths, qui se présente toujours sous forme de rectangle composé de lignes et de colonnes.
Pour une matrice, on note généralement \(A = (a_{ij})\), où \(i\) indique la ligne et \(j\) la colonne. Par exemple, si on écrit :
\( \displaystyle A = \begin{pmatrix} 3 & 5 \\ 2 & 1 \end{pmatrix} \)
Ici, on a 2 lignes et 2 colonnes, donc une matrice « carrée » d’ordre 2. Mais une matrice peut très bien avoir plus de lignes que de colonnes (ou l’inverse), et ça se note avec la dimension \( m \times n \) : \(m\) lignes et \(n\) colonnes. On appelle la diagonale principale la suite des termes \(a_{ii}\) pour \(i\) de 1 à \(n\).
Exercice 1
Dans la matrice suivante, indique le nombre de lignes, de colonnes et précise si elle est carrée :
\( \displaystyle M = \begin{pmatrix} 0 & 4 & -2 \\ 3 & 1 & 7 \end{pmatrix} \)
Voir la correction
Elle a 2 lignes et 3 colonnes, donc dimension \(2 \times 3\), ce n’est pas une matrice carrée (car il faudrait 2 lignes et 2 colonnes ou 3 lignes et 3 colonnes).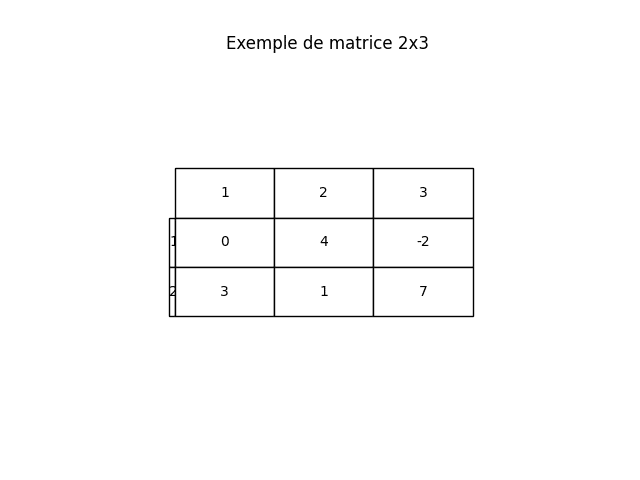
1.2 Opérations élémentaires sur les matrices
Supposons que tu aies deux matrices de même taille, comme deux tableaux de scores dans Mario Kart. Tu peux les additionner simplement : il suffit d’additionner les coefficients qui se trouvent à la même place !
Par exemple, pour deux matrices \( A = \begin{pmatrix}1&2\\3&4\end{pmatrix} \) et \( B = \begin{pmatrix}2&1\\0&3\end{pmatrix} \), leur somme est : \( A+B = \begin{pmatrix}1+2 & 2+1 \\ 3+0 & 4+3\end{pmatrix} = \begin{pmatrix}3 & 3 \\ 3 & 7\end{pmatrix} \).
On peut aussi multiplier une matrice par un nombre (appelé scalaire). Si tu multiplies chaque score par 2 pour doubler les points, tu obtiens \(2A = \begin{pmatrix}2&4\\6&8\end{pmatrix}\). Ces opérations sont commutatives (pour les additions : \(A+B=B+A\)), associatives ((\(A+B)+C=A+(B+C)\)), et distributives par rapport au scalaire (\(k(A+B)=kA+kB\)).
Exercice 2
Calcule \(A+B\) et \(3A\) pour les matrices suivantes :
\(A = \begin{pmatrix}1 & -2\\0 & 5\end{pmatrix}\), \(B = \begin{pmatrix}2 & 3\\4 & -1\end{pmatrix}\)
Voir la correction
\(A+B = \begin{pmatrix}1+2 & -2+3 \\ 0+4 & 5+(-1)\end{pmatrix} = \begin{pmatrix}3 & 1 \\ 4 & 4\end{pmatrix}\)\(3A = \begin{pmatrix}3 \times 1 & 3 \times -2 \\ 3 \times 0 & 3 \times 5\end{pmatrix} = \begin{pmatrix}3 & -6 \\ 0 & 15\end{pmatrix}\)
1.3 Systèmes d’équations linéaires
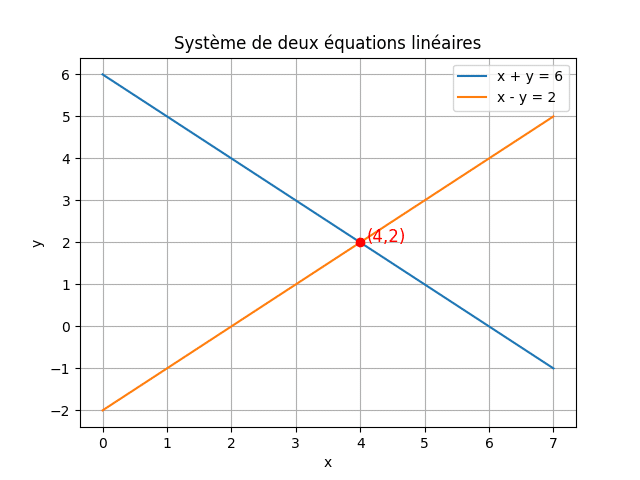
Supposons que tu cherches deux nombres dont la somme fait 6 et la différence vaut 2. C’est un système d’équations linéaires :
\( \begin{cases} x + y = 6 \\ x – y = 2 \end{cases} \)
Ici, il y a 2 équations et 2 inconnues (\(x\) et \(y\)). On appelle une solution tout couple \((x, y)\) qui vérifie les deux équations. Il peut y avoir une unique solution (« déterminé »), aucune solution (système incompatible), ou une infinité de solutions (système compatible indéterminé).
Exercice 3
Résous le système précédent.
Voir la correction
On additionne les deux équations :\(x + y + x – y = 6 + 2 donc 2x = 8 donc x = 4\)
On remplace dans la 1re équation : \(4 + y = 6 donc y = 2\).
Donc la solution est \((x, y) = (4, 2)\).
1.4 Passage du système à la matrice
Les maths aiment les raccourcis. Pour les systèmes, on note tout avec des matrices : la matrice des coefficients (\(A\)), le vecteur des inconnues (\(X\)), et le vecteur des constantes (\(B\)). Un système comme :
\( \begin{cases} 2x + 3y = 7 \\ x – y = 1 \end{cases} \)
s’écrit sous la forme : \( AX = B \), où :
\(A = \begin{pmatrix} 2 & 3 \\ 1 & -1 \end{pmatrix}\), \(X = \begin{pmatrix} x \\ y \end{pmatrix}\), \(B = \begin{pmatrix} 7 \\ 1 \end{pmatrix}\)
Cet encodage en matrice permet d’utiliser des outils puissants (calculs automatiques, méthodes de résolution) et rend la manipulation très rapide, surtout pour des systèmes plus gros !
L’avantage ? En appliquant des opérations sur les lignes, on peut résoudre le système de façon super efficace ! Par exemple, soustraire 3 fois la première ligne à la deuxième élimine \(x\).
Exercice 5
Résous ce système sous forme matricielle par combinaison des lignes.
Voir la correction
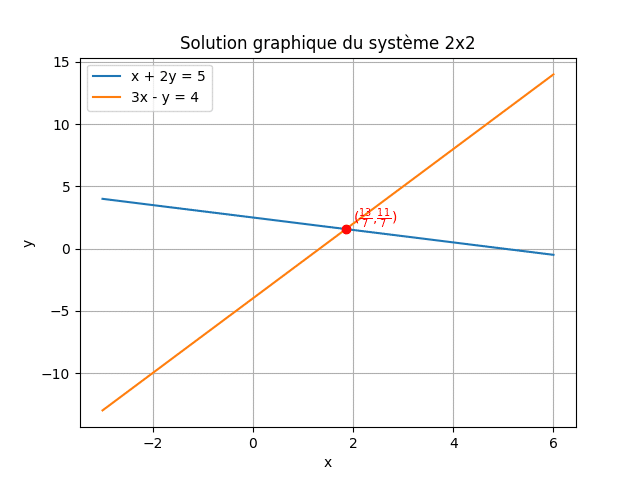
Première ligne : \(1x + 2y = 5\)Deuxième ligne moins 3 × première : \( (3x – y) – 3(1x + 2y) = 4 – 3 \times 5 \rightarrow 3x – y – 3x – 6y = 4 – 15 donc -7y = -11 donc y = \frac{11}{7}\)
Remplacer dans première équation : \(x + 2 \times \frac{11}{7} = 5 donc x = 5 – \frac{22}{7} = \frac{35-22}{7} = \frac{13}{7}\)
Solution unique : \( x = \frac{13}{7}, y = \frac{11}{7} \)
Exercices récapitulatifs
Voici cinq exercices pour t’entraîner. N’hésite pas à vérifier chaque correction !
Exercice 1
Indique la dimension et la nature des matrices suivantes :
a. \(A = \begin{pmatrix}2 & 1\end{pmatrix}\)
b. \(B = \begin{pmatrix} 4 \\ 6 \end{pmatrix} \)
c. \(C = \begin{pmatrix}1 & 0\\2 & 3\end{pmatrix}\)
Voir la correction
a. \(1 \times 2\), matrice ligneb. \(2 \times 1\), matrice colonne
c. \(2 \times 2\), matrice carrée
Exercice 2
Additionne \( D = \begin{pmatrix} 2 & -1 \\ 0 & 5 \end{pmatrix} \) et \( E = \begin{pmatrix} 1 & 4 \\ 3 & -2 \end{pmatrix} \).
Voir la correction
\(D + E = \begin{pmatrix} 2+1 & -1+4 \\ 0+3 & 5+(-2)\end{pmatrix} = \begin{pmatrix} 3 & 3 \\ 3 & 3\end{pmatrix}\)Exercice 3
Résous le système \( \begin{cases} x + y = 8 \\ x – y = 2 \end{cases} \).
Voir la correction
Addition : \(2x = 10 donc x = 5\).\(y = 8 – 5 = 3\).
Exercice 4
Écris la matrice augmentée du système \( \begin{cases} 3x + y = 0 \\ 2x – y = 4 \end{cases} \).
Voir la correction
\(\left(\begin{array}{cc|c}3 & 1 & 0 \\ 2 & -1 & 4 \end{array}\right)\)Exercice 5
Résous : \( \begin{cases} x + 3y = 7 \\ 2x – y = 1 \end{cases} \), par la méthode matricielle.
Voir la correction
Multiplier la 2e par 1, la 1re par 2 :\(2(x + 3y) – (2x – y) = 2 \times 7 – 1 donc 2x + 6y – 2x + y = 14 – 1 donc 7y = 13 donc y = \frac{13}{7}\)
\(x = 7 – 3 \times \frac{13}{7} = 7 – \frac{39}{7} = \frac{49-39}{7} = \frac{10}{7}\)
Différentes méthodes de résolution des exercices
Méthode par substitution
Le principe de la substitution
Imaginons qu’on a deux équations à deux inconnues, comme :
\( \left\{ \begin{array}{l} x + y = 4 \\ 2x – y = 1 \\ \end{array} \right. \)
L’idée ? Isoler une variable dans une équation, puis remplacer dans la seconde !
Exercice 1
Résoudre le système suivant par substitution :
\( \left\{ \begin{array}{l}
x + y = 4 \\
2x – y = 1 \\
\end{array} \right. \)
Voir la correction
On isole \( y \) dans la 1ère équation : \( y = 4 – x \). On remplace dans la 2e : \( 2x – (4 – x) = 1 \Rightarrow 2x – 4 + x = 1 \Rightarrow 3x = 5 \Rightarrow x = \frac{5}{3} \). Puis \( y = 4 – \frac{5}{3} = \frac{12}{3} – \frac{5}{3} = \frac{7}{3} \). Donc la solution est : \( x = \frac{5}{3},~y = \frac{7}{3} \).Pourquoi ça marche ? Parce qu’en remplaçant, on simplifie le système à une seule inconnue, super facile à résoudre ! Mais dès qu’il y a plus de deux inconnues, ça devient rapidement lourd…
Méthode par combinaison linéaire (élimination)
Le principe de l’élimination
L’élimination aide à faire disparaître une des variables, en combinant les équations (somme ou différence). C’est comme de la « magie » mathématique : obtenir facilement une équation à une seule inconnue !
Exercice 2
Et pour un système en 3 inconnues ?
\( \left\{ \begin{array}{l}
x + y + z = 6 \\
2x – y + z = 3 \\
-x + 3y + 2z = 14 \\
\end{array} \right. \)
Voir la correction
On peut chercher à éliminer \( y \). Additionnons (1) et (2) : \( (x + y + z) + (2x – y + z) = 6 + 3 \Rightarrow 3x + 2z = 9 \) … (4) On peut aussi former une autre combinaison, mais ici, finissons avec (4) et la 3eme eq. Exprimer \( x \) en fonction de \( z \) via (4) : \( x = \frac{9 – 2z}{3} \). Reporter dans (1) : \( \frac{9-2z}{3} + y + z = 6 \Longrightarrow y = 6 – z – \frac{9-2z}{3} = \frac{18-3z-9+2z}{3} = \frac{9-z}{3} \) Finalement, avec la 3e équation, on obtient : \( -\frac{9-2z}{3} + 3\cdot\frac{9-z}{3} + 2z = 14 \) Calculer à la main (on simplifie) puis trouver : \( z = 2 \), \( x = \frac{9-4}{3} = \frac{5}{3} \), \( y = \frac{9-2}{3} = \frac{7}{3} \).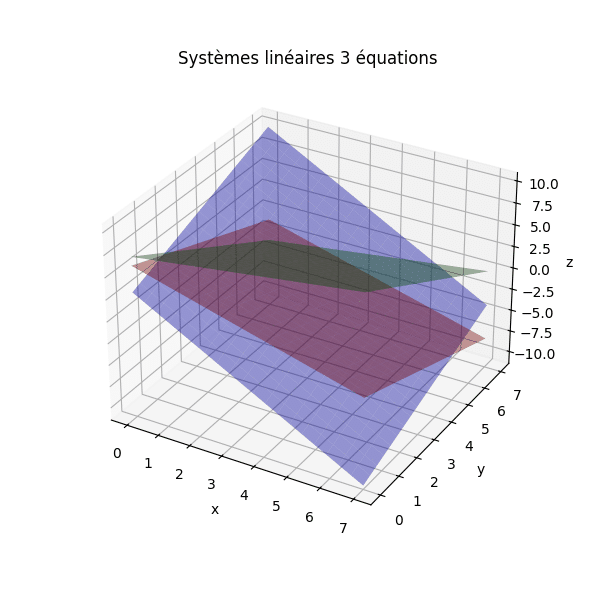
Super utile pour des systèmes 3×3 ou plus ! Mais attention, ça peut vite être long à la main…
Méthode de la matrice inverse
Quand utiliser l’inverse matricielle ?
Dès que tu as un système carré (\( n = n \)), tu peux penser à la matrice inverse, SI la matrice est inversible (\( \det(A) \neq 0 \)). On résout alors simplement : \( X = A^{-1}B \).
Exercice 4
Résoudre :
\( \left\{ \begin{array}{l}
x + 2y = 3 \\
3x + 4y = 7 \\
\end{array} \right. \)
Voir la correction
\( A = \begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix} \), \( B = \begin{pmatrix} 3 \\ 7 \end{pmatrix} \). Le déterminant : \( 1\times4 – 2\times3 = 4-6 = -2 \neq 0 \). Inverse : \( A^{-1} = \frac{1}{-2} \begin{pmatrix} 4 & -2 \\ -3 & 1 \end{pmatrix} = \begin{pmatrix} -2 & 1 \\ 1.5 & -0.5 \end{pmatrix} \). \( X = A^{-1}B = \begin{pmatrix} -2 & 1 \\ 1.5 & -0.5 \end{pmatrix} \begin{pmatrix} 3 \\ 7 \end{pmatrix} = \begin{pmatrix} -6+7 \\ 4.5-3.5 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} \). Donc : \( x=1,~y=1 \).Exercices de niveau progressif
3.1 Niveau 1 : petits systèmes 2×2
Exercice 1 : substitution simple
Voici un exemple pour démarrer en douceur. Tu dois résoudre le système suivant :
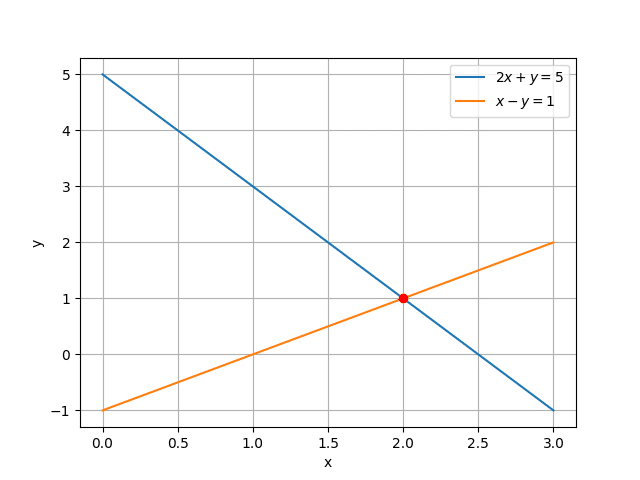
\[ \begin{cases} 2x + y = 5 \\ x – y = 1 \end{cases} \]Petite astuce : commence par exprimer \( y \) avec la deuxième équation. Placer ça sur un graphique aide souvent à « voir » ce qu’on fait !
Voir la correction
On exprime \( y \) grâce à la seconde équation : \( y = x – 1 \). On remplace dans la première : \( 2x + (x – 1) = 5 \Rightarrow 3x = 6 \Rightarrow x = 2 \). Puis, \( y = 2 – 1 = 1 \). Réponse : \( x = 2 \), \( y = 1 \).Garde en tête : dans les petits systèmes, les pièges classiques sont : – Confondre les lignes et colonnes dans les matrices ; – Perdre de vue l’interprétation graphique (pense à dessiner si tu bloques !)
3.2 Niveau 2 : systèmes 3×3 de base
Exercice 3 : elimination linéaire classique
On monte en gamme :
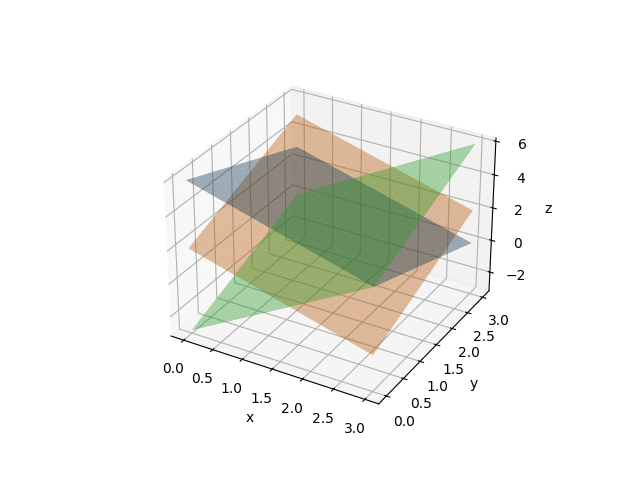
\[ \begin{cases} x + y + z = 6 \\ x – y + z = 2 \\ 2x + y – z = 3 \end{cases} \]Zéro panique ! Essaie d’éliminer d’abord \( z \) pour réécrire le système comme un 2×2, puis finalise.
Voir la correction
On additionne (1) et (2) : \( (x + y + z) + (x – y + z) = 6 + 2 \Rightarrow 2x + 2z = 8 \Rightarrow x + z = 4 \) On soustrait (2) à (1) : \( (x + y + z) – (x – y + z) = 6 – 2 \Rightarrow 2y = 4 \Rightarrow y = 2 \) Avec \( x + z = 4 \) et \( y = 2 \). On remplace \( y \) dans (3) : \( 2x + 2 – z = 3 \Rightarrow 2x – z = 1 \) On a donc : \( x + z = 4 \) \( 2x – z = 1 \) Addition : \( (x + z) + (2x – z) = 4 + 1 \Rightarrow 3x = 5 \Rightarrow x = \frac{5}{3} \) Puis \( z = 4 – x = 4 – \frac{5}{3} = \frac{12}{3} – \frac{5}{3} = \frac{7}{3} \) Enfin, \( y = 2 \)Exercice 4 : calcul de matrice inverse 3×3
Utilisons la matrice inverse pour résoudre ce système :
\[ \begin{cases} 2x + y + z = 7 \\ x + 2y + z = 8 \\ x + y + 2z = 9 \end{cases} \]Pose la matrice \( A \) (coef devant \( x, y, z \)), trouve \( A^{-1} \), puis \( X = A^{-1}B \).
Voir la correction
On écrit \( A = \begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{pmatrix} \), \( B = \begin{pmatrix} 7 \\ 8 \\ 9 \end{pmatrix} \). Après calcul, \( A^{-1} = \frac{1}{4}\begin{pmatrix} 3 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 & 3 \end{pmatrix} \). \( X = A^{-1}B = \frac{1}{4} \begin{pmatrix} 3 \times 7 – 1 \times 8 – 1 \times 9 \\ -1 \times 7 + 3 \times 8 – 1 \times 9 \\ -1 \times 7 – 1 \times 8 + 3 \times 9 \end{pmatrix} = \frac{1}{4} \begin{pmatrix} 21 – 8 – 9 \\ -7 + 24 – 9 \\ -7 – 8 + 27 \end{pmatrix} = \frac{1}{4} \begin{pmatrix} 4 \\ 8 \\ 12 \end{pmatrix} \) \( X = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \) donc \( x=1, y=2, z=3 \)Pour éviter les erreurs : vérifie l’inversibilité de la matrice (déterminant non nul !)
3.3 Niveau 3 : exercices mixtes
Exercice 5 : choix de la méthode la plus efficace
Face au système suivant, choisis toi-même la méthode la plus rapide :
\[ \begin{cases} x + 3y = 4 \\ 2x + 6y = 8 \end{cases} \]💡 Indice : compare le nombre d’équations et analyse si tu peux simplifier ton travail.
Voir la correction
La deuxième équation est un multiple de la première ! Donc, il y a une infinité de solutions : \( x + 3y = 4 \), donc \( x = 4 – 3y \), où \( y \) reste libre.Exercice 6 : système paramétré (compatibilité et étude du rang)
Résous et discute la compatibilité du système :
\[ \begin{cases} x + y = a \\ 2x + 2y = b \end{cases} \]Voir la correction
Si \( b = 2a \), il y a une infinité de solutions (les deux équations sont proportionnelles). Sinon, pas de solution (système incompatible).3.4 Niveau 4 : applications contextuelles
Exercice 7 : problème de mélanges chimiques
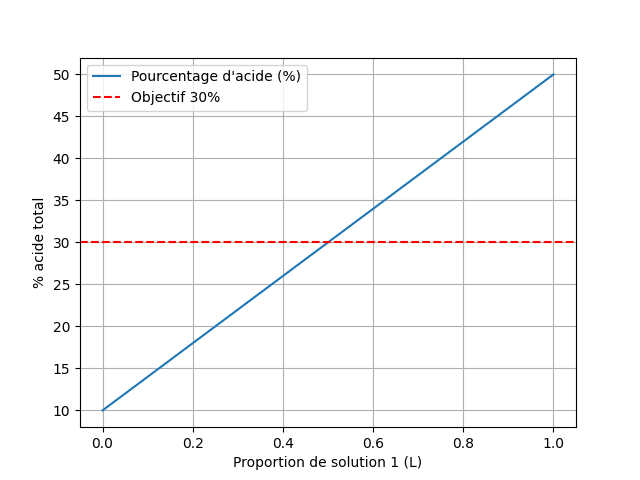
On souhaite réaliser 1 litre d’un mélange contenant 30% d’acide et 70% d’eau, en mélangeant deux solutions : l’une à 50% d’acide, l’autre à 10%. Quelles quantités de chaque solution faut-il utiliser ?
Voir la correction
Soit \( x \) la quantité (en L) de solution à 50% et \( y \) celle à 10%. On veut \( x + y = 1 \), et \( 0.5x + 0.1y = 0.3 \). \( x = 0.5 \), \( y = 0.5 \).3.5 Fiches de correction et conseils
Corrigés détaillés pour chaque exercice
Retiens bien que chaque étape doit être justifiée (isolement, remplacement, manipulation matricielle). Surligne dans ton brouillon l’étape qui te paraît cruciale : c’est celle qu’il ne faut surtout pas zapper pendant l’épreuve !
Rappels de vérification
Astuce : remplace toujours les solutions trouvées dans les équations de départ. Si ça colle, tu peux souffler… Sinon, recommence, tu as sûrement loupé une étape de calcul ou un signe.
Conseils pour préparer le bac
Avant le bac, entraîne-toi à résoudre un maximum de situations variées (systèmes à 2, 3 inconnues, à paramètres…). Et surtout, ne néglige ni la rédaction soignée, ni la vérification. Courage et confiance : à force de pratique, ces systèmes deviennent (presque) naturels !











