Dans cet article nous faisons le point avec toi sur un élément central de ton programme de spécialité mathématiques, la continuité de fonction. De quoi être un peu plus à l’aise dans cette matière bien souvent compliquée.
C’est Leonhard Euler (1707- 1783), qui le premier, a imaginé le principe de continuité d’une fonction.
Notion de continuité
Évidemment, une fonction ne peut être continue que là où elle est définie.
Euler expliquait la continuité de manière instinctive : une fonction continue est une fonction dont la courbe représentatrice peut être tracée sans lever le crayon.
Là où le bât blesse, c’est qu’une fonction peut très bien être continue sur \([1;3]\) mais pas sur \(]-\infty;+\infty[\). C’est pourquoi il faut toujours parler de continuité sur un intervalle bien précis.
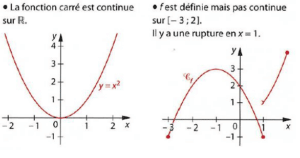
Pour être exhaustif, il faut maintenant aborder la continuité en un point.
L’image de \(a\) est \(3\). Selon la définition d’Euler, on comprend que cette fonction n’est pas continue en \(a\) puisqu’on ne peut pas se rapprocher à gauche du point \(a\) puis à droite (ou inversement) sans lever le crayon.
Finalement, instinctivement, on dira qu’une fonction est continue en \(a\) si je peux la tracer sans lever le crayon au voisinage de \(a\) (c’est-à-dire proche de \(a\)), seulement si elle définit au voisinage de \(a\). En effet, si on prend la même fonction en retirant la première partie de la fonction, alors elle est continue en \(a\) puisque définie sur \([2;5]\).
Définition de la continuité
Définition générale
Soit \(f\) une fonction définie sur un intervalle \(I\) contenant un réel \(a\).
- \(f\) est continue en \(a\) si et seulement si : \(\lim \limits_{x \to a} f(x) = f(a)\).
- \(f\) est continue sur \(I\) si \(f\) est continue en tout point de \(I\).
Cas individuel
- Les fonctions \(x \mapsto |x|\), \(x \mapsto x^n (n\in \mathbb{N})\) et plus généralement les fonctions polynômes sont continues sur \(\mathbb{R}\).
- Les fonctions \(x \mapsto sin \; x\) et \(x \mapsto cos \; x\) sont continues sur \(\mathbb{R}\).
- La fonction \(x \mapsto \sqrt x\) est continue sur \([0; +\infty[\).
- La fonction \(x \mapsto \frac{1}{x}\) est continue sur \(]-\infty;0[\) et sur \(]0;+\infty[\).
Remarque
- Les flèches d’un tableau de variation traduisent la continuité et la stricte monotonie de la fonction sur l’intervalle considéré.
- Une fonction dérivable sur un intervalle est continue sur ce même intervalle.
Théorème des Valeurs Intermédiaires (TVI)
Soit \(f\) fonction définie sur \(I\) et \(a\) et \(b\) éléments de \(I\).
Si \(f\) est continue sur \(I\) alors :
pour tout réel \(k\) compris entre \(f(a)\) et \(f(b)\),
il existe au moins un réel \(x_0\) compris entre \(a\) et \(b\) tel que : \(f(x_0) = k\).
Autrement dit, toutes « les valeurs intermédiaires » entre les deux images de \(a\) et de \(b\) sont atteintes.
Dans le cas où \(f\) est strictement monotone sur l’intervalle \([a;b]\) alors le réel \(x_0\) est unique.
Les erreurs à éviter
- Une fonction dérivable en un point est continue en ce point mais la réciproque est fausse. Par exemple les fonctions racine carrée et valeur absolue sont continues en \(0\) mais non dérivables en ce point.
- La continuité est condition suffisante mais non nécessaire pour appliquer le TVI. En effet, on peut imaginer une fonction où \(k\in [a;b]\) admette un antécédent sans nécessairement que \(f\) ne soit continue sur \([a;b]\).