Dans cet article, nous allons explorer ensemble le monde fascinant des logarithmes décimaux. Tu verras, ce n’est pas aussi compliqué qu’il y paraît, et c’est super utile dans plein de domaines, de la science à la musique. Imagine pouvoir simplifier des calculs complexes ou comprendre comment on mesure l’intensité d’un son ou l’acidité d’une solution : c’est exactement ce que les logarithmes nous permettent de faire ! Dans cet article, nous allons commencer par les bases, découvrir les propriétés des logarithmes décimaux, apprendre des méthodes pour résoudre des exercices, et enfin, nous entraîner avec des exercices corrigés. Alors, prêt à plonger dans cette aventure mathématique ? C’est parti !
Définition du logarithme décimal
1.1 Fonction exponentielle \(10^x\)
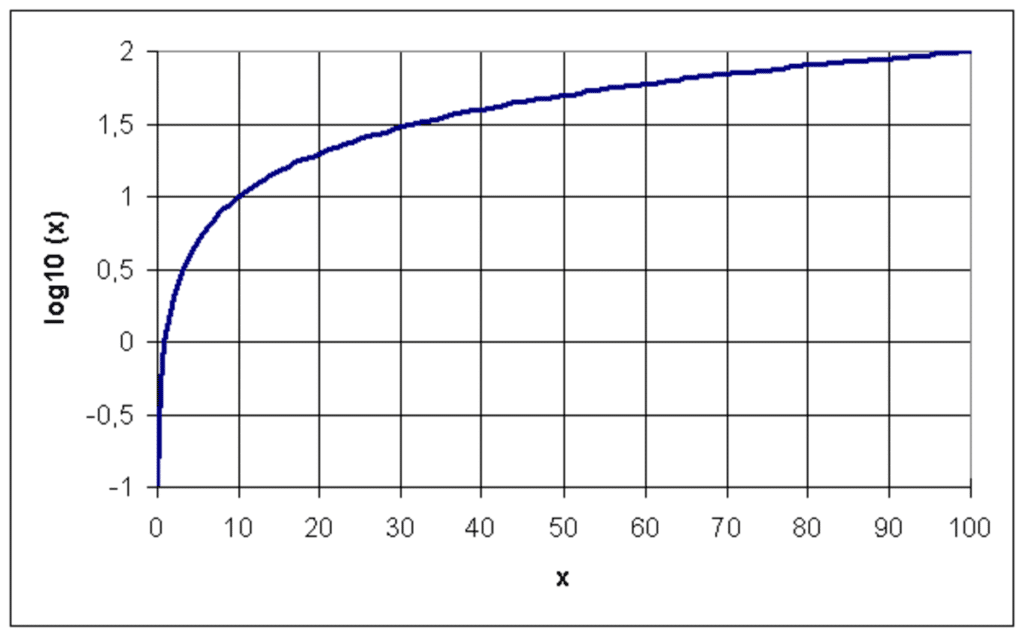
La fonction exponentielle de base 10 est définie comme \(f(x) = 10^x\). Cette fonction est croissante et définie pour tous les nombres réels \(x\). Elle est essentielle pour comprendre les logarithmes, car elle est directement liée à la fonction logarithme.
Pour exemple :
- Pour \(x = 2\), \(10^2 = 100\)
- Pour \(x = -1\), \(10^{-1} = 0.1\)
1.2 Logarithme décimal
Le logarithme décimal, noté \(\log\) ou parfois \(\log_{10}\), est la fonction réciproque de la fonction exponentielle \(10^x\). Cela signifie que si \(y = 10^x\), alors \(x = \log(y)\). Autrement dit, le logarithme décimal nous donne l’exposant auquel il faut élever 10 pour obtenir un nombre donné.
Pour mieux comprendre, voici quelques exemples :
- \(\log(100) = 2\) parce que \(10^2 = 100\)
- \(\log(0.01) = -2\) parce que \(10^{-2} = 0.01\)
- \(\log(1) = 0\) parce que \(10^0 = 1\)
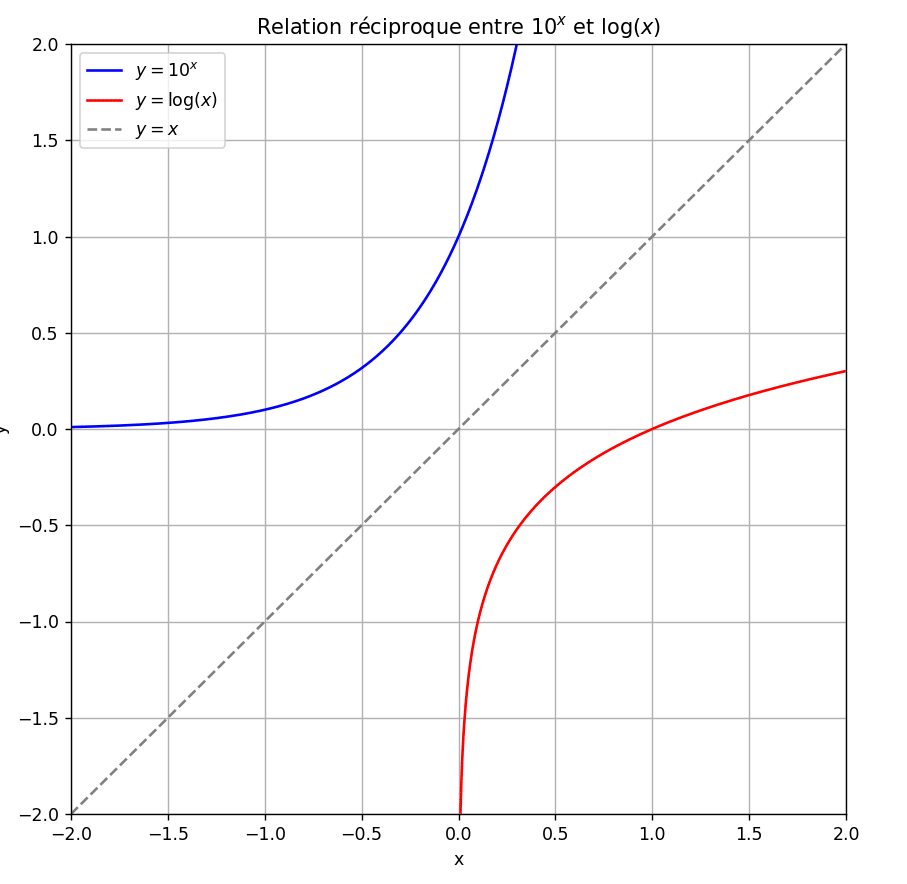
1.3 Relation réciproque entre \(10^x\) et \(\log(x)\)
La fonction logarithme décimal est la réciproque de la fonction exponentielle de base 10. Cela signifie que les deux fonctions annulent mutuellement leurs effets lorsqu’on les compose (qu’on applique l’une puis l’autre) :
\[ 10^{\log(x)} = x \quad \text{et} \quad \log(10^x) = x \]
Cette relation réciproque est cruciale pour résoudre des équations exponentielles et logarithmiques.
1.4 Échelle logarithmique sur l’axe y
Une échelle logarithmique sur l’axe y est utilisée pour représenter des données qui couvrent une grande plage de valeurs. Au lieu d’augmenter de manière linéaire (par additions), chaque marque sur l’axe y augmente par multiplication (généralement par 10 pour une base 10). Cela permet de visualiser des données qui varient exponentiellement ou qui couvrent plusieurs ordres de grandeur.
Pourquoi utiliser une échelle logarithmique ?
1. Représentation de grandes gammes de valeurs :
Les échelles logarithmiques permettent de visualiser des valeurs extrêmement grandes ou petites sur un même graphique. Par exemple, en astronomie, les distances peuvent varier de quelques kilomètres à des milliards de kilomètres.
2. Visualisation des relations multiplicatives :
Elles permettent de voir facilement des relations multiplicatives. Par exemple, sur une échelle logarithmique, une augmentation de 1 sur l’axe correspond à une multiplication par 10 (pour une base 10).
Exemples d’utilisation :
- Échelle de Richter : Utilisée pour mesurer la magnitude des tremblements de terre. Chaque augmentation d’une unité sur l’échelle de Richter correspond à une multiplication par 10 de l’amplitude des ondes.
- Mesures de pH : Le pH est une mesure logarithmique de l’acidité ou de la basicité d’une solution. Un changement d’une unité de pH représente un changement d’un facteur 10 dans la concentration en ions hydrogène.
- Décibels : Le niveau de pression sonore est mesuré en décibels (dB), qui est une unité logarithmique. Une augmentation de 10 dB correspond à une intensité sonore multipliée par 10.
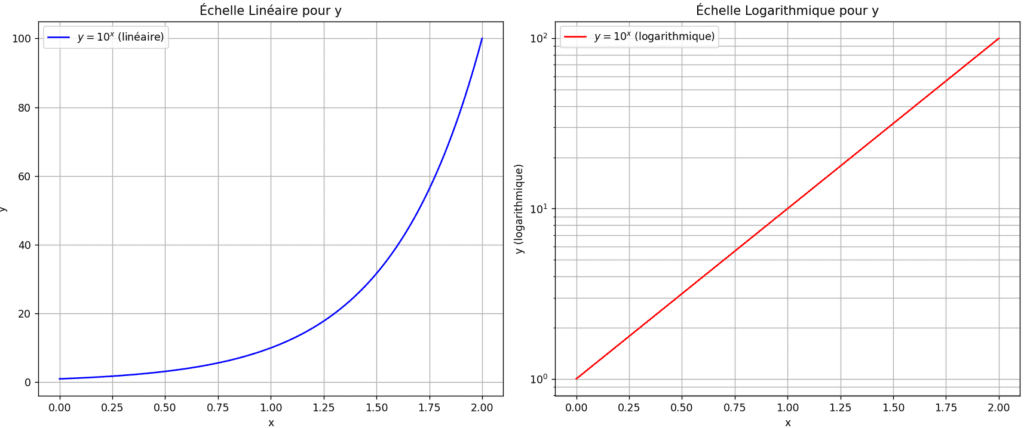
Le graphique de gauche montre une fonction exponentielle avec une échelle linéaire pour l’axe y, où la courbe monte rapidement. Le graphique de droite montre la même fonction exponentielle mais avec une échelle logarithmique pour l’axe y, transformant la courbe en une ligne droite. Cela montre comment une échelle logarithmique peut « linéariser » une fonction exponentielle, facilitant ainsi l’analyse de données qui couvrent plusieurs ordres de grandeur.
Pour mieux comprendre, essayez de convertir les valeurs suivantes en échelle logarithmique (base 10) :
1. Convertir 1000 en échelle logarithmique.
2. Convertir 0.01 en échelle logarithmique.
3. Convertir 1000000 en échelle logarithmique.
Voir les réponses
1. \(\log(10000) = 4\)
2. \(\log(0.1) = -1\)
3. \(\log(10) = 1\)
Propriétés du logarithme décimal
Les logarithmes décimaux ont plusieurs propriétés intéressantes qui les rendent très utiles en mathématiques. En voici quelques-unes :
2.1 Propriété du Produit
La propriété du produit stipule que le logarithme d’un produit est la somme des logarithmes des facteurs. Mathématiquement, cela s’exprime comme suit :
\[ \log(ab) = \log(a) + \log(b) \]
Cette propriété est particulièrement utile pour transformer des produits en sommes, ce qui peut simplifier des calculs complexes.
👉🏻 Exemple :
Calculons \(\log(100)\) en utilisant cette propriété.
Si nous savons que 100 peut être écrit comme \(10 \times 10\), alors :
\[ \log(100) = \log(10 \times 10) = \log(10) + \log(10) = 1 + 1 = 2 \]
🤔 Exercice :
Calculez \(\log(200)\) en utilisant la propriété du produit, sachant que 200 peut être écrit comme \(2 \times 100\).
Voir la réponse
\[ \log(200) = \log(2 \times 100) = \log(2) + \log(100) \approx 0.3010 + 2 = 2.3010 \]
2.2 Propriété du Quotient
La propriété du quotient stipule que le logarithme d’un quotient est la différence des logarithmes du numérateur et du dénominateur. Mathématiquement, cela s’exprime comme suit :
\[ \log\left(\frac{a}{b}\right) = \log(a) – \log(b) \]
Cette propriété est très utile pour transformer des divisions en soustractions.
Exemple :
Calculons \(\log(5)\) en utilisant cette propriété, sachant que 5 peut être écrit comme \(\frac{10}{2}\).
\[ \log(5) = \log\left(\frac{10}{2}\right) = \log(10) – \log(2) \approx 1 – 0.3010 = 0.6990 \]
Exercice
Calculez \(\log(50)\) en utilisant la propriété du quotient, sachant que 50 peut être écrit comme \(\frac{100}{2}\).
Voir la réponse
\[ \log(50) = \log\left(\frac{100}{2}\right) = \log(100) – \log(2) \approx 2 – 0.3010 = 1.6990 \]
2.3 Propriété de la Puissance
La propriété de la puissance stipule que le logarithme d’une puissance est l’exposant multiplié par le logarithme de la base (c’est une conséquence de la propriété de multiplication). Mathématiquement, cela s’exprime comme suit :
\[ \log(a^b) = b \cdot \log(a) \]
Cette propriété permet de transformer des calculs de puissances en multiplications plus simples.
👉🏻 Exemple :
Calculons \(\log(1000)\) en utilisant cette propriété, sachant que 1000 peut être écrit comme \(10^3\).
\[ \log(1000) = \log(10^3) = 3 \cdot \log(10) = 3 \times 1 = 3 \]
🤔 Exercice :
Calculez \(\log(10000)\) en utilisant la propriété de la puissance, sachant que 10000 peut être écrit comme \(10^4\).
Voir la réponse
\[ \log(10000) = \log(10^4) = 4 \cdot \log(10) = 4 \times 1 = 4 \]
2.4 Propriété de Bijectivité
La fonction logarithme est bijective. Cela signifie qu’elle établit une correspondance unique entre chaque nombre positif et un nombre réel. En d’autres termes, chaque nombre positif a une et une seule image par la fonction logarithme, et chaque nombre réel est l’image d’un et un seul nombre positif.
👉🏻 Explication :
- Injectivité : Si \(\log(a) = \log(b)\), alors \(a = b\). Cela signifie que deux nombres différents ne peuvent pas avoir le même logarithme.
- Surjectivité : Pour tout nombre réel \(y\), il existe un nombre strictement positif \(x\) tel que \(\log(x) = y\). Cela signifie que tout nombre réel est le logarithme d’un nombre positif strictement.
Cette propriété est utile pour résoudre des équations logarithmiques, car elle nous permet de déduire que si \(\log(a) = \log(b)\), alors \(a = b\) sans autre considération.
👉🏻 Exemple :
Résoudre l’équation \(\log(x) = \log(5)\).
1. Puisque la fonction logarithme est injective, on peut déduire que \(x = 5\).
🤔 Exercices d’application :
1. Résoudre \(\log(x) = \log(7)\).
2. Résoudre \(\log(x+3) = \log(8)\).
3. Résoudre \(\log(x^2) = \log(16)\).
4. Résoudre \(\log(2x) = \log(10)\).
5. Résoudre \(\log(x/2) = \log(4)\).
Voir les réponses
1. \(x = 7\)
2. \(x = 5\)
3. \(x = \pm4\)
4. \(x = 5\)
5. \(x = 8\)
La propriété de bijectivité nous aide à résoudre simplement de nombreuses équations logarithmiques en utilisant le fait que \(\log(a) = \log(b)\) implique \(a = b\).
Ces propriétés sont fondamentales pour travailler avec des logarithmes et simplifier des expressions complexes. Elles sont largement utilisées dans divers domaines des mathématiques et des sciences.
Les méthodes à connaitre
1. Simplification d’expressions logarithmiques
Les propriétés des logarithmes sont très utiles pour simplifier des expressions complexes. Voici un rappel des principales propriétés.
1. Produit :
\[ \log(ab) = \log(a) + \log(b) \]
Cette propriété permet de transformer un produit en une somme de logarithmes.
2. Quotient :
\[ \log\left(\frac{a}{b}\right) = \log(a) – \log(b) \]
Cette propriété permet de transformer un quotient en une différence de logarithmes.
3. Puissance :
\[ \log(a^b) = b \cdot \log(a) \]
Cette propriété permet de transformer une puissance en un multiple du logarithme.
👉🏻 Exemple :
Simplifions l’expression \(\log(8x^3y^2)\).
1. D’abord, appliquer la propriété du produit pour séparer les termes :
\[ \log(8x^3y^2) = \log(8) + \log(x^3) + \log(y^2) \]
2. Ensuite, appliquer la propriété de la puissance pour les termes avec des exposants :
\[ \log(8) + 3\log(x) + 2\log(y) \]
3. Si on connaît \(\log(8)\), on peut le laisser tel quel ou le développer en utilisant les propriétés :
\[ \log(8) = \log(2^3) = 3\log(2) \]
Ainsi, l’expression simplifiée est :
\[ 3\log(2) + 3\log(x) + 2\log(y) \]
🤔 Exercices d’application :
Simplifiez les expressions suivantes :
1. \(\log(12xy)\)
2. \(\log\left(\frac{a^2b}{c}\right)\)
3. \(\log(100x^4)\)
4. \(\log\left(\frac{x^3y^2}{z}\right)\)
5. \(\log(\sqrt{x^5y^3})\)
Voir les réponses
1. \(\log(12) + \log(x) + \log(y)\)
2. \(2\log(a) + \log(b) – \log(c)\)
3. \(\log(100) + 4\log(x) = 2 + 4\log(x)\) (car \(\log(100) = 2\))
4. \(3\log(x) + 2\log(y) – \log(z)\)
5. \(\frac{5}{2}\log(x) + \frac{3}{2}\log(y)\)
2. Résolution d’équations logarithmiques simples
Les équations logarithmiques simples sont celles où le logarithme d’une expression est égal à une constante. La forme générale est :
\[ \log(x) = k \]
Pour résoudre ce type d’équation, nous utilisons la définition du logarithme. Si \(\log(x) = k\), alors par définition, \(x = 10^k\), car le logarithme et la fonction exponentielle sont des fonctions inverses.
👉🏻 Exemple :
Résoudre l’équation \(\log(x) = 3\).
1. Convertir l’équation logarithmique en sa forme exponentielle :
\[ x = 10^3 \]
2. Calculer \(10^3\) :
\[ x = 1000 \]
🤔 Exercices d’application :
Résoudre les équations suivantes :
1. \(\log(x) = 4\)
2. \(\log(x) = -2\)
3. \(\log(x) = 0\)
4. \(\log(x) = 1\)
5. \(\log(x) = -1\)
Voir les réponses
1. \(x = 10000\)
2. \(x = 0.01\)
3. \(x = 1\)
4. \(x = 10\)
5. \(x = 0.1\)
3. Résolution d’équations logarithmiques avec propriétés
Pour résoudre des équations logarithmiques où plusieurs termes logarithmiques apparaissent, nous utilisons les propriétés des logarithmes pour combiner ces termes en un seul logarithme, ce qui simplifie la résolution. Voici les étapes générales.
1. Combiner les termes logarithmiques : utiliser les propriétés du produit, du quotient et de la puissance pour combiner les logarithmes en un seul terme.
2. Égaliser les arguments : si deux logarithmes sont égaux, leurs arguments doivent être égaux (en supposant que la base est la même et positive).
3. Résoudre l’équation résultante : après avoir combiné les logarithmes, résoudre l’équation algébrique obtenue.
4. Vérifier les solutions : assure-toi que les solutions obtenues sont dans le domaine de la fonction logarithme (c’est-à-dire que l’argument du logarithme doit être positif).
👉🏻 Exemple :
Résoudre l’équation \(\log(x) + \log(2) = \log(20)\).
1. Combiner les termes logarithmiques en utilisant la propriété du produit :
\[ \log(2x) = \log(20) \]
2. Égaliser les arguments :
\[ 2x = 20 \]
3. Résoudre pour \(x\) :
\[ x = \frac{20}{2} = 10 \]
4. Vérifier que \(x = 10\) est dans le domaine (c’est-à-dire que \(x > 0\)).
🤔 Exercices d’application :
Résoudre les équations suivantes :
1. \(\log(x) + \log(3) = \log(30)\)
2. \(\log(x) – \log(2) = \log(5)\)
3. \(\log(x) + \log(4) = \log(20) + \log(2)\)
4. \(\log(x) – \log(3) + \log(2) = \log(10)\)
5. \(\log(x) + \log(5) – \log(2) = \log(25)\)
Voir les réponses
1. \(x = 10\)
2. \(x = 10\)
3. \(x = 10\)
4. \(x = 6\)
5. \(x = 10\)
4. Changement de base
Le changement de base est une technique essentielle pour résoudre des équations logarithmiques où la base du logarithme n’est pas 10 (ou la base naturelle, e). La formule pour le changement de base est :
\[ \log_b(a) = \frac{\log_k(a)}{\log_k(b)} \]
où \(k\) est une base quelconque, souvent 10 ou e pour simplifier les calculs.
👉🏻 Exemple :
Résoudre l’équation \(\log_3(x) = 2\).
1. Appliquer le changement de base pour transformer l’équation en une forme plus facile à gérer. Nous utiliserons la base 10 pour le changement de base :
\[ \frac{\log_{10}(x)}{\log_{10}(3)} = 2 \]
2. Multiplier les deux côtés par \(\log_{10}(3)\) :
\[ \log_{10}(x) = 2 \cdot \log_{10}(3) \]
3. Convertir en forme exponentielle :
\[ x = 10^{2 \cdot \log_{10}(3)} \]
4. Simplifier en utilisant les propriétés des logarithmes et des exponentielles :
\[ x = 10^{\log_{10}(3^2)} = 3^2 = 9 \]
🤔 Exercices d’application :
Résoudre les équations suivantes :
1. \(\log_2(x) = 3\)
2. \(\log_5(x) = -1\)
3. \(\log_7(x) = 0\)
4. \(\log_{1/2}(x) = -3\)
5. \(\log_x(8) = 3\)
6. \(\log_4(x) = 0.5\)
Voir les réponses
1. \(x = 8\)
2. \(x = \frac{1}{5}\)
3. \(x = 1\)
4. \(x = 8\)
5. \(x = 2\)
6. \(x = 2\)
5. Résolution d’équations logarithmiques complexes
Pour résoudre des équations logarithmiques complexes, il est souvent nécessaire de combiner plusieurs termes logarithmiques en utilisant les propriétés du produit, du quotient et de la puissance. Voici les étapes générales :
1. Combiner les termes logarithmiques : utiliser les propriétés des logarithmes pour combiner tous les termes en un seul logarithme de chaque côté de l’équation, si possible.
2. Égaliser les arguments : si les deux côtés de l’équation sont des logarithmes avec la même base, égaliser leurs arguments.
3. Résoudre l’équation résultante : après avoir égalisé les arguments, résoudre l’équation algébrique obtenue.
4. Vérifier les solutions : assure-toi que les solutions obtenues sont dans le domaine de la fonction logarithme (les arguments des logarithmes doivent être positifs).
👉🏻 Exemple :
Résoudre l’équation \(\log(x+1) + \log(x-1) = \log(12)\).
1. Combiner les termes logarithmiques en utilisant la propriété du produit :
\[ \log((x+1)(x-1)) = \log(12) \]
Simplifiez l’expression à l’intérieur du logarithme :
\[ \log(x^2 – 1) = \log(12) \]
2. Égaliser les arguments :
\[ x^2 – 1 = 12 \]
3. Résoudre pour \(x\) :
– Ajouter 1 des deux côtés :
\[ x^2 = 13 \]
– Prendre la racine carrée des deux côtés :
\[ x = \pm\sqrt{13} \]
4. Vérifier les solutions :
– Pour \(x = \sqrt{13}\) : \(x + 1 > 0\) et \(x – 1 > 0\) sont toutes deux vraies.
– Pour \(x = -\sqrt{13}\) : \(x – 1 < 0\) n’est pas valide. Ainsi, la seule solution valide est \(x = \sqrt{13}\).
🤔 Exercices d’application :
Résoudre les équations suivantes :
1. \(\log(x) + \log(x+2) = \log(24)\)
2. \(\log(x) – \log(x-3) = \log(2)\)
3. \(\log(x+5) + \log(x-1) = \log(36)\)
4. \(\log(x) + \log(x+3) = \log(28)\)
5. \(\log(x+2) – \log(x) = \log(3)\)
6. \(\log(x+3) + \log(x) = \log(28)\)
Voir les réponses
1. \(x = 4\)
2. \(x = 6\)
3. \(x = 5\)
4. \(x = 4\)
5. \(x = 3\)
6. \(x = 4\)
6. Résolution d’équations exponentielles et logarithmiques mixtes
Les équations exponentielles et logarithmiques mixtes contiennent à la fois des fonctions exponentielles et logarithmiques. La stratégie générale pour résoudre ces équations est la suivante :
1. Isoler l’exponentielle ou le logarithme : réarrange l’équation pour isoler la fonction exponentielle ou logarithmique.
2. Prendre le logarithme ou l’exponentielle des deux côtés : si l’équation contient une exponentielle, prenez le logarithme des deux côtés. Si elle contient un logarithme, passez en forme exponentielle.
3. Résoudre pour la variable : résous l’équation algébrique obtenue pour la variable.
4. Vérifier les solutions : assure-toi que les solutions obtenues satisfont le domaine des fonctions en jeu.
👉🏻 Exemple :
Résoudre l’équation \(10^x = 1000\).
1. Isoler l’exponentielle (déjà isolée dans cet exemple).
2. Prendre le logarithme des deux côtés :
\[ \log(10^x) = \log(1000) \]
3. Simplifier en utilisant la propriété \( \log(a^b) = b \log(a) \) :
\[ x \cdot \log(10) = \log(1000) \]
Puisque \(\log(10) = 1\) et \(\log(1000) = 3\), nous avons :
\[ x = 3 \]
🤔 Exercices d’application :
Résoudre les équations suivantes :
1. \(10^x = 100\)
2. \(10^{2x} = 1000\)
3. \(10^{x+1} = 1\)
4. \(10^x = 0.01\)
5. \(10^{x} = 100000\)
Voir les réponses
1. \(x = 2\)
2. \(x = 1.5\)
3. \(x = -1\)
4. \(x = -2\)
5. \(x = 5\)
7. Résolution d’inéquations logarithmiques
Résoudre une inéquation logarithmique implique de trouver les valeurs de la variable qui satisfont l’inégalité tout en respectant le domaine de la fonction logarithmique (les arguments des logarithmes doivent être positifs). Voici les étapes générales :
1. Combiner les termes logarithmiques : si possible, combine les termes logarithmiques en un seul terme de chaque côté de l’inéquation.
2. Transformer l’inéquation logarithmique en une inéquation algébrique : utilise les propriétés des logarithmes pour supprimer les logarithmes et obtenir une inéquation algébrique.
3. Résoudre l’inéquation algébrique : résous l’inéquation résultante pour la variable.
4. Vérifier le domaine et les solutions : assure-toi que les solutions satisfont les conditions du domaine (les arguments des logarithmes doivent être positifs).
👉🏻 Exemple :
Résoudre l’inéquation \(\log(x) > 1\).
1. Transformer l’inéquation logarithmique en une inéquation algébrique :
\[ x > 10^1 \]
\[ x > 10 \]
2. Vérifier le domaine : \(x > 0\) (condition nécessaire pour que le logarithme soit défini). Dans ce cas, \(x > 10\) satisfait automatiquement \(x > 0\).
Ainsi, la solution est \(x > 10\).
🤔 Exercices d’application :
Résoudre les inéquations suivantes :
1. \(\log(x) < 2\)
2. \(\log(x) + \log(2) > \log(10)\)
3. \(\log(x) – \log(3) \leq \log(2)\)
4. \(\log(x+4) \geq \log(9)\)
5. \(\log(2x) < \log(3)\)
Voir les réponses
1. \(0 < x < 100\)
2. \(x > 5\)
3. \(0 < x \leq 6\)
4. \(x \geq 5\)
5. \(0 < x < 1.5\)
Exercices d’application
Exercice 1 : Équation logarithmique simple avec vérification
👉🏻 Énoncé :
Résoudre l’équation suivante et vérifier la solution :
\[ \log(x) + \log(x-3) = \log(28) \]
👉🏻 Solution :
1. Combiner les termes logarithmiques :
Utiliser la propriété du produit pour combiner les termes :
\[ \log(x(x-3)) = \log(28) \]
2. Égaliser les arguments :
\[ x(x-3) = 28 \]
3. Résoudre l’équation quadratique :
Développez et réarrangez l’équation :
\[ x^2 – 3x – 28 = 0 \]
Utiliser la formule quadratique pour résoudre pour \(x\) :
\[ x = \frac{3 \pm \sqrt{9 + 112}}{2} = \frac{3 \pm \sqrt{121}}{2} = \frac{3 \pm 11}{2} \]
Les solutions sont :
\[ x = \frac{3 + 11}{2} = 7 \quad \text{et} \quad x = \frac{3 – 11}{2} = -4 \]
4. Vérification des solutions :
– Pour \(x = 7\) : Vérifiez que tous les arguments du logarithme sont positifs :
\[ x = 7 > 0, \quad x-3 = 4 > 0 \]
La solution \(x = 7\) est valide.
– Pour \(x = -4\) : L’argument \(x = -4\) n’est pas positif, donc cette solution est rejetée.
Donc, la seule solution valide est \(x = 7\).
Exercice 2 : Équation avec changement de base
👉🏻 Énoncé :
Résoudre l’équation suivante en utilisant un changement de base :
\[ \log_4(x) + \log_4(x-6) = 1 \]
👉🏻 Solution :
1. Combiner les termes logarithmiques :
Utiliser la propriété du produit pour combiner les termes :
\[ \log_4(x(x-6)) = 1 \]
2. Convertir l’équation en sa forme exponentielle :
\[ x(x-6) = 4^1 = 4 \]
3. Résoudre l’équation quadratique :
Développez et réarrangez l’équation :
\[ x^2 – 6x – 4 = 0 \]
Utiliser la formule quadratique pour résoudre pour \(x\) :
\[ x = \frac{6 \pm \sqrt{36 + 16}}{2} = \frac{6 \pm \sqrt{52}}{2} = \frac{6 \pm 2\sqrt{13}}{2} = 3 \pm \sqrt{13} \]
4. Vérification des solutions :
– Pour \(x = 3 + \sqrt{13}\) : Vérifiez que tous les arguments du logarithme sont positifs. Comme \(3 + \sqrt{13} > 6\) (car \(\sqrt{13} \approx 3.6\) et donc \(x \approx 6.6\)), \(x > 0\) et \(x-6 > 0\) sont vérifiés.
– Pour \(x = 3 – \sqrt{13}\) : L’argument \(x = 3 – \sqrt{13}\) est négatif car \(\sqrt{13} \approx 3.6\), donc \(x \approx -0.6\). Cette solution est rejetée.
Donc, la seule solution valide est \(x = 3 + \sqrt{13}\).
Exercice 3 : Inéquation logarithmique
👉🏻 Énoncé :
Résoudre l’inéquation suivante :
\[ \log(x+2) > \log(5x-6) \]
🤔 Solution :
1. Domaine des arguments :
Pour que les logarithmes soient définis, les arguments doivent être positifs :
\[ x+2 > 0 \quad \text{et} \quad 5x-6 > 0 \]
Cela donne :
\[ x > -2 \quad \text{et} \quad x > \frac{6}{5} \]
Comme \(\frac{6}{5} = 1.2 > -2\), la condition de domaine se réduit à \(x > 1.2\).
2. Résolution de l’inéquation :
Puisque la fonction logarithme est strictement croissante pour des bases supérieures à 1, l’inéquation \(\log(a) > \log(b)\) est équivalente à \(a > b\) (à condition que \(a\) et \(b\) soient positifs, ce qui est déjà garanti par le domaine).
Donc, nous pouvons comparer les arguments directement :
\[ x+2 > 5x-6 \]
Simplifiez l’inéquation :
\[ x + 2 > 5x – 6 \]
Soustraire \(x\) et ajouter 6 des deux côtés :
\[ 8 > 4x \]
Diviser par 4 :
\[ 2 > x \quad \text{ou} \quad x < 2 \]
3. Combinaison avec le domaine :
Nous avons trouvé que \(x > 1.2\). Par conséquent, la solution est :
\[ 1.2 < x < 2 \]