En géométrie comme en physique, l’idée intuitive de « centre » revient très souvent : le centre d’un cercle, le centre de gravité d’un objet, le point d’équilibre d’une figure. Le barycentre généralise cette notion et devient un outil extrêmement puissant à la fois pour simplifier des calculs, pour résoudre des problèmes de géométrie vectorielle et pour comprendre les équilibres physiques.
Tu as peut-être déjà rencontré le barycentre dans un contexte concret : le balancier d’une règle posée sur ton doigt, le centre de masse d’un objet, ou la moyenne pondérée en statistiques. En maths, c’est la même idée : on cherche un point qui représente une « moyenne géométrique » de plusieurs autres points pondérés.
Définition du barycentre
Soient \(A_1, A_2, …, A_n\) des points d’un plan et \(\alpha_1, \alpha_2, …\alpha_n\) des réels appelés coefficients de pondération, avec :
\(\alpha_1 + \alpha_2 + … \ \alpha_n \neq 0 \)
On appelle barycentre de l’ensemble pondéré \(\{(A_1,\alpha_1), …, (A_n,\alpha_n)\}\) le point \(G\) défini par la relation vectorielle :
\(\overrightarrow{OG} = \frac{\alpha_1 \overrightarrow{OA_1} + \alpha_2 \overrightarrow{OA_2} + \cdots + \alpha_n \overrightarrow{OA_n}}{\alpha_1 + \alpha_2 + \cdots + \alpha_n} \)
où \(O\) est un point de référence arbitraire.
On note généralement :
\(G = Bar(A_1,\alpha_1 ; A_2,\alpha_2; … ; A_n,\alpha_n\)
En d’autres termes, le barycentre est un « point moyen » qui prend en compte à la fois la position des points et les coefficients.
Cas particuliers pour mieux comprendre
- Deux points pondérés :
Le barycentre de deux points \(A\) et \(B\), pondérés par \(\alpha\) et \(\beta\), est un point \(G\) de la droite \(AB\) tel que :
\(\overrightarrow{AG} = \frac{\beta}{\alpha + \beta} \overrightarrow{AB}\)
Ainsi, si \(\alpha = \beta\), le barycentre est simplement le milieu du segment \([AB]\).
- Trois points pondérés :
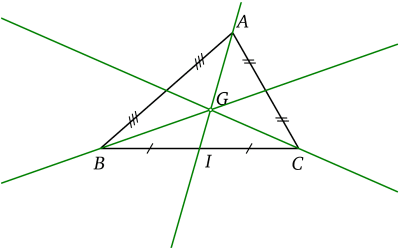
Le barycentre de trois points pondérés correspond au « centre de gravité » d’un triangle si les coefficients sont tous égaux. Par exemple,
\(G = Bar (A,1; B,1; C,1)\)
désigne le centre de gravité du triangle \(ABC\), intersection des médianes.
Interprétation géométrique
La définition du barycentre est directement inspirée de la physique. Si tu imagines que chaque point \(A_i\) est une masse placée sur le plan, alors le barycentre est exactement le centre de gravité de l’ensemble des masses.
Cette analogie est très utile :
- Plus un coefficient est grand, plus le barycentre se rapproche du point associé.
- En équilibrant les poids respectifs, on retrouve la position d’équilibre du système.
- Le barycentre se trouve toujours à l’intérieur du convexe formé par les points si tous les coefficients sont positifs.
Propriétés fondamentales du barycentre
Le barycentre possède plusieurs propriétés qui le rendent incontournable en géométrie vectorielle :
- Unicité : pour un système pondéré avec somme des coefficients non nulle, il existe toujours un unique barycentre.
- Associativité : on peut calculer le barycentre de plusieurs points en regroupant d’abord certains sous-ensembles. Cela permet de simplifier les calculs étape par étape.
- Lien avec les moyennes : le barycentre est la traduction géométrique de la moyenne pondérée que tu connais en statistiques.
Exemple numérique :
Prenons les points \(A(0,0)\) et \(B(2,0)\), avec coefficients 1 et 3. Le barycentre est :
\(x_G = \frac{1 \times 0 + 3 \times 2}{1 + 3} = \frac{6}{4} = 1.5\)
Donc \(G(1,5;0)\), ce qui est logique : le barycentre est plus proche du point \(B\) qui « pèse plus lourd ».
Applications en géométrie
- Centre de gravité d’un triangle : intersection des médianes, barycentre des trois sommets pondérés de façon égale.
- Subdivision de polygones : on peut trouver le barycentre d’un quadrilatère en le scindant en deux triangles, puis en prenant à nouveau le barycentre.
- Résolution de problèmes vectoriels : les équations d’équilibre ou les recherches de points particuliers dans un repère se simplifient grâce à la formule barycentrique.
- Lien avec la physique : le barycentre traduit directement la notion de centre de masse d’un système matériel.
Exercices
Exercice 1 :
Soit \(A(0,0)\), \(B(4,0)\) et \(C(0,2)\). Déterminer le barycentre \(G\) de l’ensemble \(\{(A,1),(B,1),(C,1)\}\).
Exercice 2 :
Soient \(A(1,2)\) et \(B(5,6)\), pondérés respectivement par 2 et 3. Trouve le barycentre \(G\).
Correction
Exercice 1 :
On a trois points pondérés également. Le barycentre est donc le centre de gravité du triangle \(ABC\).
Coordonnées :
\(x_G = \frac{0 + 4 + 0}{3} = \frac{4}{3}\), \(y_G = \frac{0 + 0 + 2}{3} = \frac{2}{3}\)
Ainsi, \(G(\frac{4}{3},\frac{2}{3})\).
Exercice 2 :
On applique la formule :
\(x_G = \frac{2 \times 1 + 3 \times 5}{2 + 3} = \frac{2 + 15}{5} = \frac{17}{5} = 3.4\)
\(y_G = \frac{2 \times 2 + 3 \times 6}{5} = \frac{4 + 18}{5} = \frac{22}{5} = 4.4\)
Ainsi, \(G(3,4 ; 4,4)\). On observe que le point est plus proche de \(B\), associé au poids le plus élevé.
La notion de barycentre en géométrie est une généralisation précieuse de la moyenne pondérée. Elle relie naturellement les mathématiques à la physique, en incarnant à la fois une idée de calcul pratique et une intuition d’équilibre. Comprendre cette notion te permet de simplifier des calculs vectoriels, de résoudre plus facilement des problèmes de géométrie, et de préparer l’étude des centres de gravité en sciences physiques.