Comprendre et interpréter les graphiques de fonctions

L’interprétation des graphiques de fonctions est une compétence fondamentale en mathématiques, particulièrement utile pour comprendre et analyser des phénomènes dans divers domaines scientifiques et économiques. Dans cet article, nous allons explorer les bases de la représentation graphique des fonctions, discuter des méthodes pour les interpréter correctement, et appliquer ces connaissances à travers une série d’exercices corrigés. Attention simplement, car à la fin de l’article, je te parle de concavité, de convexité, de points d’inflexion… que tu n’as peut-être encore jamais vus! Si c’est le cas, pas de panique, ignore simplement cette partie, tu le verras plus tard.

Présentation du graphique de fonction et définitions

Un graphique de fonction est une représentation visuelle d’une fonction mathématique. Imagine que tu as une machine magique qui, pour chaque nombre que tu y mets (appelé l’entrée), te donne un autre nombre (la sortie). Le graphique de cette fonction est simplement un dessin qui montre toutes ces paires entrée-sortie sous la forme de points sur un plan. Par exemple, la fonction qui associe à chaque nombre son carré peut être représentée par une courbe appelée parabole.

Tout savoir sur la fonction de production et la combinaison productive

Composantes d’un graphique

Un graphique de fonction se compose de plusieurs éléments clés :

👉🏻 Axes : Le graphique est construit sur deux axes perpendiculaires. L’axe horizontal est appelé l’axe des abscisses (généralement noté \(x\)), et l’axe vertical est l’axe des ordonnées (généralement noté \(y\)).

👉🏻 Échelle et unités : Chaque axe a une échelle qui détermine comment les unités sont représentées. Par exemple, chaque centimètre sur l’axe des \(x\) pourrait représenter une unité.

👉🏻 Quadrants : Les axes divisent le plan en quatre régions appelées quadrants, numérotées de I à IV dans le sens inverse des aiguilles d’une montre à partir du quadrant en haut à droite.

Définitions essentielles

👉🏻 Domaine et image : Le domaine d’une fonction est l’ensemble de toutes les valeurs d’entrée possibles (\(x\)), tandis que l’image est l’ensemble des valeurs de sortie (\(f(x)\)).

👉🏻 Fonction croissante/décroissante : Une fonction est croissante sur un intervalle si, lorsque \(x\) augmente, \(f(x)\) augmente aussi. Elle est décroissante si \(f(x)\) diminue lorsque \(x\) augmente.

👉🏻 Maximum et minimum : Ce sont les points les plus hauts et les plus bas sur le graphique de la fonction dans un intervalle donné.

Pour mieux comprendre, imagine que tu suives le trajet d’une voiture. La distance parcourue (en kilo mètres) est une fonction du temps (en heures). Si tu traces ce trajet sur un graphique, l’axe des \(x\) représente le temps et l’axe des \(f(x)\) représente la distance. Tu peux voir à quelle vitesse la voiture se déplace en observant à quel point la courbe est raide à certains moments.

Voici un exemple de graphique pour une fonction quadratique :

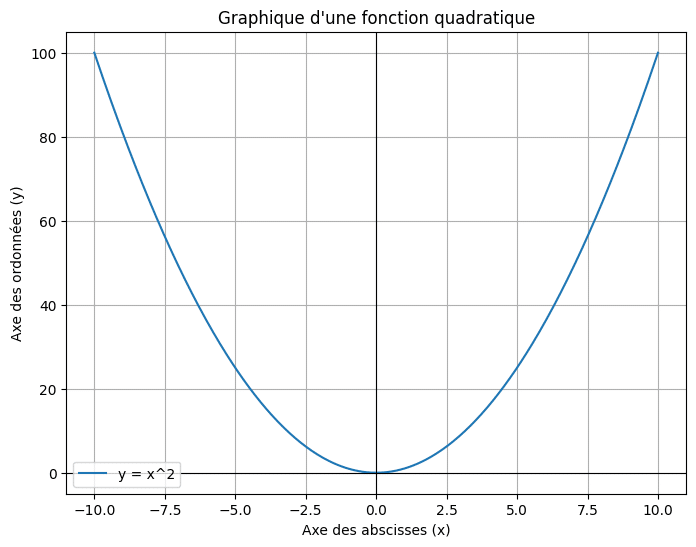
Ce graphique montre la parabole définie par \(y = x^2\). Comme tu peux le voir, la courbe est symétrique par rapport à l’axe des ordonnées et elle a un minimum en \(x = 0\), où la fonction atteint sa valeur la plus basse.

Tout savoir sur la fonction inverse

Méthodes / questions types

Méthode 1 : Lecture des coordonnées (point par point)

1. Situation : La lecture des coordonnées sur un graphique de fonction permet de déterminer la valeur de la fonction pour une valeur donnée de \( x \) et vice versa. Cette méthode est essentielle pour comprendre les relations définies par la fonction.

2. Démarche à suivre :

1. Identifie le point sur le graphique de la fonction \( f \) dont tu souhaites connaître les coordonnées.

2. Trace une ligne verticale depuis ce point jusqu’à l’axe des abscisses pour déterminer la valeur de \( x \).

3. Trace une ligne horizontale depuis ce point jusqu’à l’axe des ordonnées pour déterminer la valeur de \( f(x) \).

4. Les coordonnées du point sont \( (x, f(x)) \).

3. Pourquoi ça marche : Chaque point sur le graphique de la fonction représente une paire \( (x, f(x)) \) qui satisfait l’équation de la fonction. En traçant des lignes depuis le point jusqu’aux axes, tu retrouveras ces valeurs.

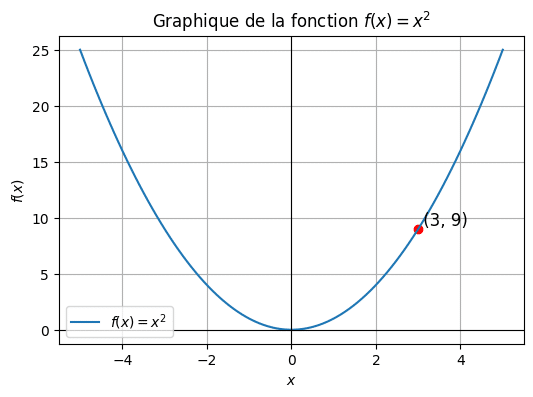
4. Exemple d’application avec exercice corrigé :

Considère le graphique suivant qui représente la fonction \( f(x) = x^2 \). Détermine les coordonnées du point où \( x = 3 \).

Correction : Pour \( x = 3 \), on trace une ligne verticale jusqu’à la courbe, et horizontalement jusqu’à l’axe des ordonnées pour trouver \( f(x) = 9 \). Donc, les coordonnées sont (3, 9).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Détermine les coordonnées du point où \( x = -2 \) sur le graphique de \( f(x) = x^2 \).

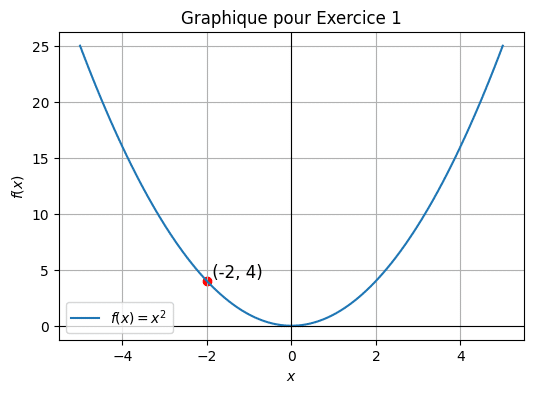
Voir la correction

Pour \( x = -2 \), nous trouvons \( f(x) = (-2)^2 = 4 \). Donc, les coordonnées sont (-2, 4).

👉🏻 Exercice 2 : Trouve les coordonnées du point sur le graphique de \( f(x) = x + 2 \) où \( x = 1 \).

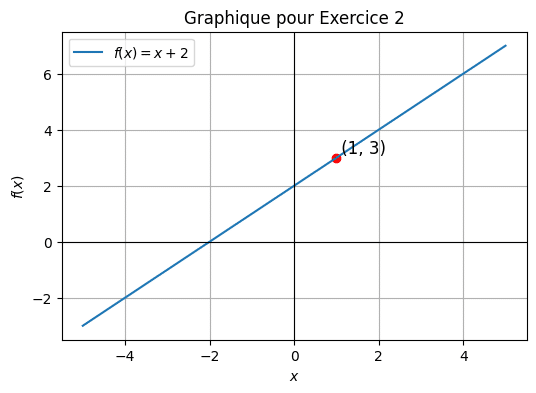
Voir la correction

Pour \( x = 1 \), nous avons \( f(x) = 1 + 2 = 3 \). Donc, les coordonnées sont (1, 3).

Exercice 3 : Détermine les coordonnées du point où \( f(x) = 16 \) sur le graphique de \( f(x) = x^2 \).

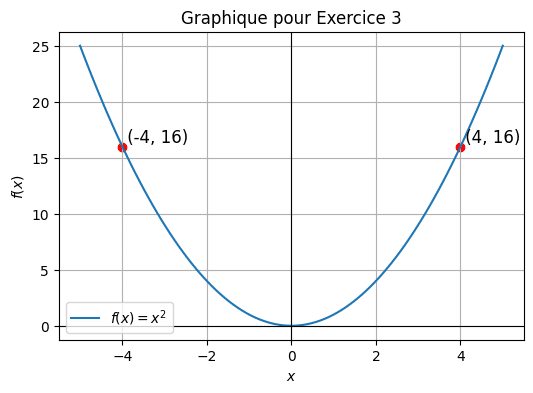
Voir la correction

Pour \( f(x) = 16 \), nous avons \( x^2 = 16 \), donc \( x = \pm 4 \). Les coordonnées sont (4, 16) et (-4, 16).

Exercice 4 : Trouve les coordonnées du point sur le graphique de \( f(x) = 2x + 1 \) où \( x = -1 \).

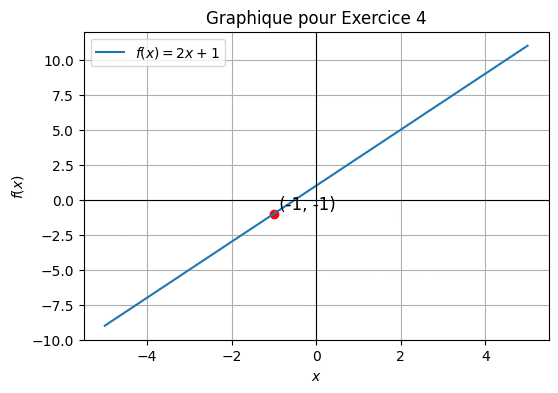
Voir la correction

Pour \( x = -1 \), nous avons \( f(x) = 2(-1) + 1 = -1 \). Donc, les coordonnées sont (-1, -1).

Exercice 5 : Détermine les coordonnées du point où \( f(x) = 0 \) sur le graphique de \( f(x) = x^2 – 4 \).

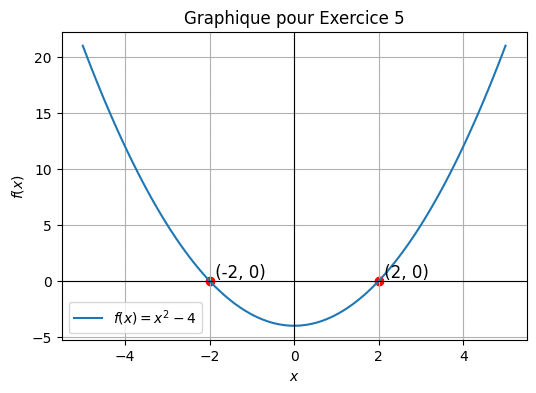
Voir la correction

Pour \( f(x) = 0 \), nous avons \( x^2 – 4 = 0 \), donc \( x = \pm 2 \). Les coordonnées sont (2, 0) et (-2, 0).

Comment réussir l’épreuve de spécialité maths au bac ?

Méthode 2 : Détermination du domaine et de l’image d’une fonction

1. Situation : La détermination du domaine et de l’image d’une fonction est cruciale pour comprendre les limites de la fonction. Le domaine représente toutes les valeurs d’entrée possibles (x) pour lesquelles la fonction est définie, tandis que l’image représente toutes les valeurs de sortie possibles (f(x)).

2. Démarche à suivre :

1. Domaine : Identifie toutes les valeurs de \( x \) pour lesquelles la fonction \( f(x) \) est définie. Pour les fonctions polynomiales, le domaine est généralement tous les nombres réels. Cependant, pour les fonctions rationnelles ou radicales, il peut y avoir des restrictions.

2. Image : Pour déterminer l’image, recherchez toutes les valeurs de \( f(x) \). Cela peut nécessiter de trouver les maxima et minima de la fonction, ou de comprendre son comportement asymptotique.

3. Pourquoi ça marche : Le domaine et l’image sont des aspects fondamentaux de la définition d’une fonction. Le domaine indique où la fonction « vit » sur l’axe des x, tandis que l’image montre toutes les valeurs y que la fonction peut atteindre.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = \sqrt{x + 3} \). Détermine son domaine et son image.

Correction :

• Domaine : La fonction est définie lorsque l’expression sous la racine est non négative, donc \( x + 3 \geq 0 \) implique \( x \geq -3 \). Le domaine est \([-3, +\infty)\).

• Image : La fonction racine donne toujours une valeur non négative, donc l’image est \([0, +\infty)\).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Détermine le domaine et l’image de la fonction \( f(x) = x^2 – 4 \).

Voir la correction

Domaine : Tous les nombres réels, car il s’agit d’une fonction polynomiale. Image : \([-4, +\infty)\).

👉🏻 Exercice 2 : Trouvez le domaine de la fonction \( f(x) = \frac{1}{x – 2} \) et son image.

Voir la correction

Domaine : Tous les nombres réels sauf \(x = 2\). Image : Tous les nombres réels sauf \(y = 0\).

👉🏻 Exercice 3 : Pour la fonction \( f(x) = |x + 1| \), détermine le domaine et l’image.

Voir la correction

Domaine : Tous les nombres réels. Image : \([0, +\infty)\).

👉🏻 Exercice 4 : Détermine le domaine et l’image de la fonction \( f(x) = -2x^2 + 3 \).

Voir la correction

Domaine : Tous les nombres réels. Image : \((-\infty, 3]\).

👉🏻 Exercice 5 : Trouve le domaine de la fonction \( f(x) = \sqrt{4 – x^2} \) et son image.

Voir la correction

Domaine : \([-2, 2]\). Image : \([0, 2]\).

Méthode 3 : Taux de variation et pente

1. Situation : Le taux de variation ou la pente d’une fonction en un point donne une indication de la rapidité à laquelle la fonction augmente ou diminue à cet endroit. Cela est particulièrement utile pour comprendre le comportement local de la fonction et pour identifier les sections de croissance ou de décroissance.

2. Démarche à suivre :

1. Choisir deux points : Sélectionne deux points distincts sur le graphique de la fonction, idéalement proches l’un de l’autre pour une estimation locale précise.

2. Calculer la variation : Détermine la variation en y (delta y) et en x (delta x) entre ces deux points.

3. Calculer la pente : La pente (ou taux de variation) est donnée par le rapport de la variation en y sur la variation en x : \(\frac{\Delta y}{\Delta x}\).

3. Pourquoi ça marche : La pente entre deux points sur une ligne droite représente le changement vertical par rapport au changement horizontal, ce qui définit la raideur ou l’inclinaison de la ligne. Dans le contexte des fonctions, cela donne une estimation de la dérivée, qui mesure comment la fonction change à un point donné.

4. Exemple d’application avec exercice corrigé :

Considère la fonction linéaire \( f(x) = 2x + 3 \). Calcule la pente de cette fonction entre les points d’abscisses 1 et 3.

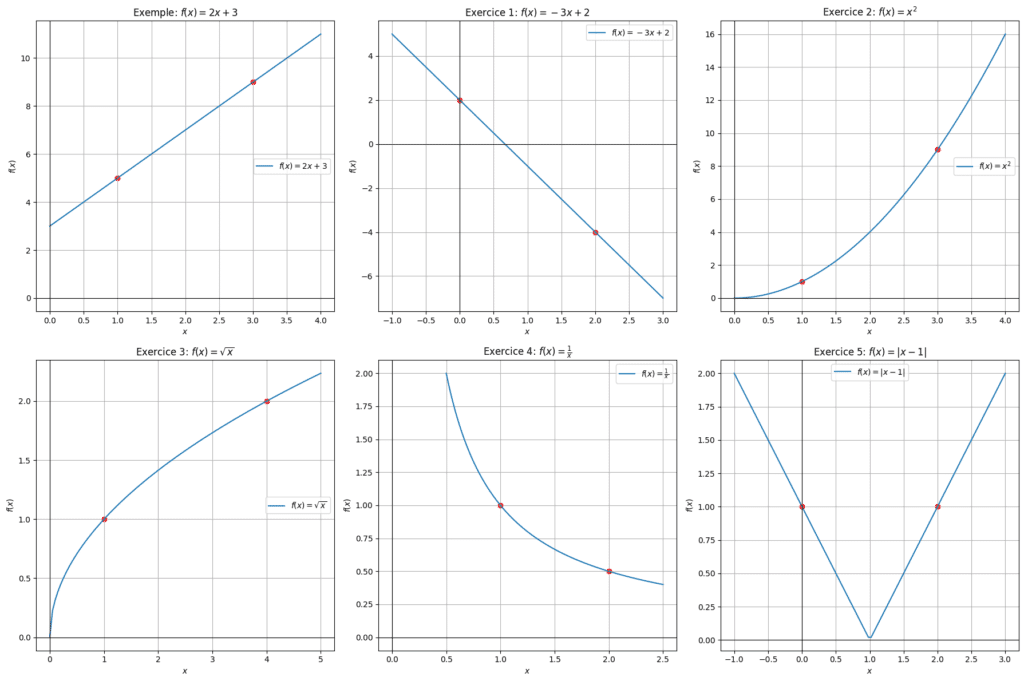
Correction :

Pour calculer la pente entre les points d’abscisses 1 et 3 :

• Coordonnées des points :

Pour \( x = 1 \), \( f(x) = 2(1) + 3 = 5 \)

Pour \( x = 3 \), \( f(x) = 2(3) + 3 = 9 \)

La variation en y est \( 9 – 5 = 4 \) et la variation en x est \( 3 – 1 = 2 \). Ainsi, la pente est \(\frac{4}{2} = 2\).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Calcule la pente de la fonction \( f(x) = -3x + 2 \) entre les points d’abscisses 0 et 2.

Voir la correction

– Coordonnées des points : (0, 2) et (2, -4) – Pente : \(\frac{-4 – 2}{2 – 0} = \frac{-6}{2} = -3\)

👉🏻 Exercice 2 : Trouve la pente de la fonction \( f(x) = x^2 \) entre les points d’abscisses 1 et 3.

Voir la correction

– Coordonnées des points : (1, 1) et (3, 9) – Pente : \(\frac{9 – 1}{3 – 1} = \frac{8}{2} = 4\)

👉🏻 Exercice 3 : Détermine la pente de la fonction \( f(x) = \sqrt{x} \) entre les points d’abscisses 1 et 4.

Voir la correction

– Coordonnées des points : (1, 1) et (4, 2) – Pente : \(\frac{2 – 1}{4 – 1} = \frac{1}{3}\)

👉🏻 Exercice 4 : Calcule la pente de la fonction \( f(x) = \frac{1}{x} \) entre les points d’abscisses 1 et 2.

Voir la correction

– Coordonnées des points : (1, 1) et (2, 0.5) – Pente : \(\frac{0.5 – 1}{2 – 1} = \frac{-0.5}{1} = -0.5\)

👉🏻 Exercice 5 : Trouve la pente de la fonction \( f(x) = |x – 1| \) entre les points d’abscisses 0 et 2.

Voir la correction

– Coordonnées des points : (0, 1) et (2, 1) – Pente : \(\frac{1 – 1}{2 – 0} = 0\)

Méthode 4 : Équation de la tangente à une courbe

1. Situation : Trouver l’équation de la tangente à une courbe en un point donné est une application pratique de la dérivée d’une fonction. La tangente à une courbe en un point est une droite qui touche la courbe à ce point sans la couper, et sa pente est égale à la dérivée de la fonction en ce point.

2. Démarche à suivre :

1. Trouver la dérivée de la fonction : Calcule la dérivée de la fonction pour obtenir la pente de la tangente en tout point.

2. Calculer la pente en un point : Évalue la dérivée au point d’abscisse donné pour obtenir la pente de la tangente en ce point.

3. Utiliser la formule point-pente : Utilise la formule de l’équation de la droite sous forme point-pente pour trouver l’équation de la tangente.

3. Pourquoi ça marche : La dérivée d’une fonction à un point donné donne le taux de variation instantané de la fonction à ce point, qui est aussi la pente de la tangente à la courbe à ce point. La formule point-pente permet de déterminer l’équation de cette tangente en utilisant cette pente et le point de tangence.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = x^2 – 4x + 3 \). Trouve l’équation de la tangente à la courbe au point d’abscisse 2.

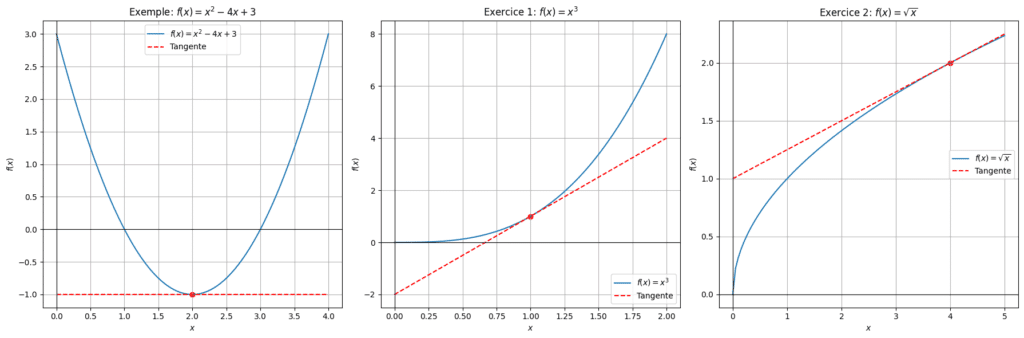
Correction :

1. Calculer la dérivée : La dérivée de \( f(x) \) est \( f'(x) = 2x – 4 \).

2. Calculer la pente en x = 2 : \( f'(2) = 2(2) – 4 = 0 \), donc la pente est 0.

3. Équation de la tangente : Puisque la pente est 0, la tangente est une ligne horizontale passant par le point où x = 2, et y = (2)^2 – 4(2) + 3 = -1. L’équation de la tangente est donc \( y = -1 \).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Trouve l’équation de la tangente à la courbe \( f(x) = x^3 \) au point d’abscisse 1.

Voir la correction

– Dérivée : \( f'(x) = 3x^2 \). Pente en x = 1 : \( f'(1) = 3(1)^2 = 3 \). – Point de tangence : (1,1). – Équation : \( y – 1 = 3(x – 1) \) donc \( y = 3x – 2 \).

👉🏻 Exercice 2 : Trouve l’équation de la tangente à la courbe \( f(x) = \sqrt{x} \) au point d’abscisse 4.

Voir la correction

– Dérivée : \( f'(x) = \frac{1}{2\sqrt{x}} \). Pente en x = 4 : \( f'(4) = \frac{1}{2\sqrt{4}} = \frac{1}{4} \). – Point de tangence : (4,2). – Équation : \( y – 2 = \frac{1}{4}(x – 4) \) donc \( y = \frac{1}{4}x + 1 \).

Méthode 5 : Étude des variations d’une fonction

1. Situation : L’étude des variations d’une fonction permet de comprendre comment la fonction évolue en fonction de sa variable. Cela inclut la détermination des intervalles où la fonction est croissante ou décroissante, ainsi que l’identification des extrema locaux (minima et maxima).

2. Démarche à suivre :

1. Calculer la dérivée : Trouver la dérivée première de la fonction pour étudier son signe.

2. Trouver les points critiques : Résoudre l’équation où la dérivée est égale à zéro ou indéfinie pour trouver les points critiques.

3. Étudier le signe de la dérivée : Analyser le signe de la dérivée autour des points critiques pour déterminer les intervalles de croissance et de décroissance.

4. Conclure sur les variations : Résumer les résultats pour décrire les variations de la fonction.

3. Pourquoi ça marche : La dérivée d’une fonction donne des informations sur la pente de cette fonction. Une dérivée positive indique une croissance de la fonction, tandis qu’une dérivée négative indique une décroissance. Les points critiques, où la dérivée est nulle ou indéfinie, peuvent indiquer des extrema locaux.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = x^3 – 3x^2 + 4 \). Étudie les variations de cette fonction.

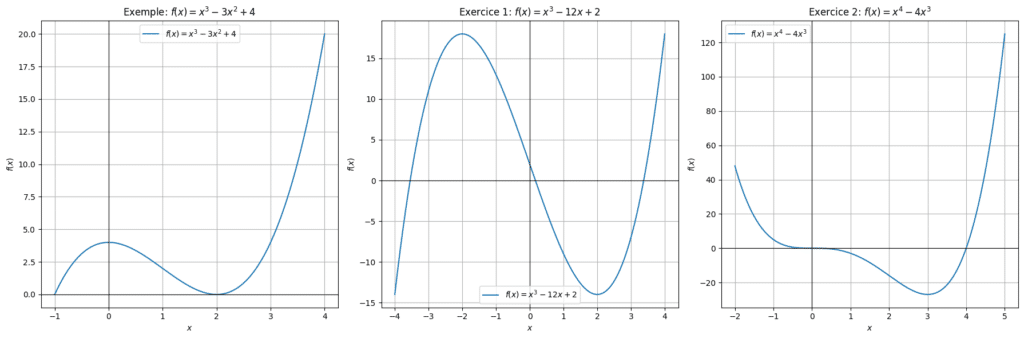
Correction :

1. Calculer la dérivée : La dérivée de \( f(x) \) est \( f'(x) = 3x^2 – 6x \).

2. Trouver les points critiques : Résoudre \( 3x^2 – 6x = 0 \) donne \( x(3x – 6) = 0 \), donc \( x = 0 \) et \( x = 2 \).

3. Étudier le signe de la dérivée :

• Pour \( x < 0 \), testons \( x = -1 \): \( f'(-1) = 3(-1)^2 – 6(-1) = 9 \) (positif).
• Pour \( 0 < x < 2 \), testons \( x = 1 \): \( f'(1) = 3(1)^2 – 6(1) = -3 \) (négatif).
• Pour \( x > 2 \), testons \( x = 3 \): \( f'(3) = 3(3)^2 – 6(3) = 9 \) (positif).

4. Conclure sur les variations :

• La fonction est croissante sur \(]-\\infty, 0]\) et \([2, +\infty[\).
• La fonction est décroissante sur \([0, 2]\).
• Points critiques : x=0 est un maximum local et x=2 est un minimum local.

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Étudie les variations de la fonction \( f(x) = x^3 – 12x + 2 \).

Voir la correction

1. Calculer la dérivée : \( f'(x) = 3x^2 – 12 \). 2. Trouver les points critiques : Résoudre \( 3x^2 – 12 = 0 \) donne \( x = \pm2 \). 3. Étudier le signe de la dérivée : – Pour \( x < -2 \), testons \( x = -3 \): \( f'(-3) = 3(-3)^2 – 12 = 15 \) (positif). – Pour \( -2 < x 2 \), testons \( x = 3 \): \( f'(3) = 3(3)^2 – 12 = 15 \) (positif). 4. Conclure : – La fonction est croissante sur \(]-\infty, -2]\) et \([2, +\infty[\) et décroissante sur \([-2, 2]\). – Points critiques : x=-2 est un maximum local et x=2 est un minimum local.

👉🏻 Exercice 2 : Étudie les variations de la fonction \( f(x) = x^4 – 4x^3 \).

Voir la correction

1. Calculer la dérivée : \( f'(x) = 4x^3 – 12x^2 \). 2. Trouver les points critiques : Résoudre \( 4x^3 – 12x^2 = 0 \) donne \( x = 0 \) et \( x = 3 \). 3. Étudier le signe de la dérivée : – Pour \( x < 0 \), testons \( x = -1 \): \( f'(-1) = 4(-1)^3 – 12(-1)^2 = -4 – 12 = -16 \) (négatif). – Pour \( 0 < x 3 \), testons \( x = 4 \): \( f'(4) = 4(4)^3 – 12(4)^2 = 256 – 192 = 64 \) (positif). 4. Conclure : – La fonction est croissante sur \([3, +\infty[\) et décroissante sur \(]-\infty, 0]\) et \([0, 3]\). – Point critique : x=3 est un minimum local et x=0 est un point d’inflexion.

Méthode 6 : Intersections avec les axes

1. Situation : Trouver les points où le graphique d’une fonction croise les axes des abscisses (x) et des ordonnées (y) est une étape fondamentale dans l’analyse des fonctions. Cela permet de déterminer les racines de la fonction et son ordonnée à l’origine.

2. Démarche à suivre :

1. Intersection avec l’axe des x (racines) : Résoudre l’équation \( f(x) = 0 \) pour trouver les valeurs de \( x \) où la fonction croise l’axe des abscisses.

2. Intersection avec l’axe des y : Évaluer \( f(0) \) pour trouver le point où la fonction croise l’axe des ordonnées.

3. Pourquoi ça marche : Les intersections avec les axes fournissent des informations cruciales sur le comportement de la fonction. Les racines (intersections avec l’axe des x) montrent où la fonction vaut zéro, tandis que l’ordonnée à l’origine (intersection avec l’axe des y) montre la valeur de la fonction lorsque \( x = 0 \).

4. Exemple d’application avec exercice corrigé :

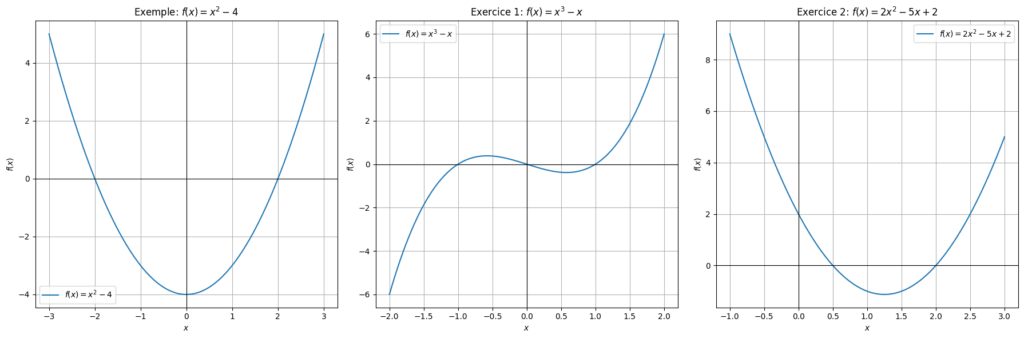
Considère la fonction \( f(x) = x^2 – 4 \). Trouvez ses intersections avec les axes.

Correction :

1. Intersection avec l’axe des x : Résoudre \( x^2 – 4 = 0 \) donne \( x = \pm 2 \). Donc, les points d’intersection sont \((-2, 0)\) et \((2, 0)\).

2. Intersection avec l’axe des y : Évaluer \( f(0) = 0^2 – 4 = -4 \). Donc, le point d’intersection est \((0, -4)\).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Trouve les intersections avec les axes de la fonction \( f(x) = x^3 – x \).

Voir la correction

1. Intersection avec l’axe des x : Résoudre \( x^3 – x = 0 \) donne \( x(x^2 – 1) = 0 \), donc \( x = -1, 0, 1 \). Les points d’intersection sont \((-1, 0)\), \((0, 0)\), et \((1, 0)\). 2. Intersection avec l’axe des y : Évaluer \( f(0) = 0^3 – 0 = 0 \). Donc, le point d’intersection est \((0, 0)\).

👉🏻 Exercice 2 : Trouve les intersections avec les axes de la fonction \( f(x) = 2x^2 – 5x + 2 \).

Voir la correction

1. Intersection avec l’axe des x : Résoudre \( 2x^2 – 5x + 2 = 0 \) donne \( x = \frac{5 \pm \sqrt{25 – 16}}{4} \), donc \( x = 0.5 \) et \( x = 2 \). Les points d’intersection sont \((0.5, 0)\) et \((2, 0)\). 2. Intersection avec l’axe des y : Évaluer \( f(0) = 2(0)^2 – 5(0) + 2 = 2 \). Donc, le point d’intersection est \((0, 2)\).

Méthode 7 : Symétrie et périodicité

1. Situation : La symétrie et la périodicité sont des propriétés importantes des fonctions qui peuvent simplifier leur étude. Une fonction peut être paire, impaire, ou périodique, et ces propriétés peuvent aider à comprendre son comportement global.

2. Démarche à suivre :

Symétrie :

• Fonction paire : Vérifier si \( f(-x) = f(x) \) pour tous \( x \) dans le domaine de la fonction.
• Fonction impaire : Vérifier si \( f(-x) = -f(x) \) pour tous \( x \) dans le domaine de la fonction.

Périodicité :

• Fonction périodique : Vérifier s’il existe un nombre positif \( T \) tel que \( f(x + T) = f(x) \) pour tous \( x \) dans le domaine de la fonction. Le plus petit \( T \) est appelé la période.

3. Pourquoi ça marche : La symétrie peut réduire l’analyse d’une fonction à un seul côté de l’axe des ordonnées, tandis que la périodicité permet de se concentrer sur une seule période de la fonction, car le comportement se répète.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = x^2 \). Détermine si elle est paire, impaire, ou ni l’un ni l’autre.

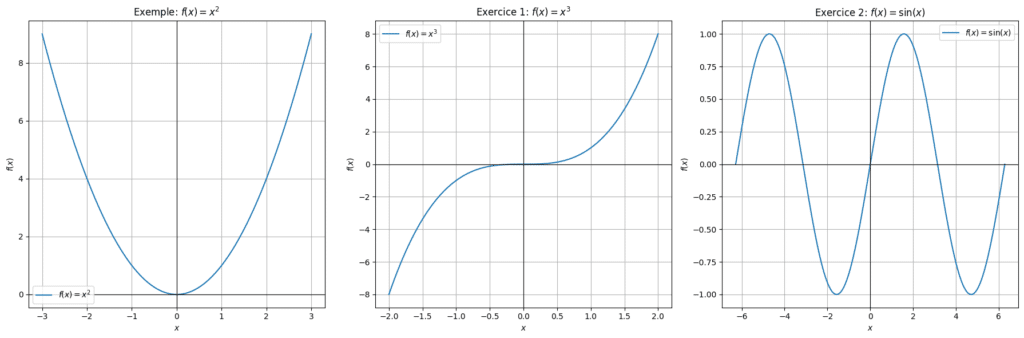
Correction :

1. Symétrie : Vérifions si \( f(-x) = (-x)^2 = x^2 = f(x) \). Donc, \( f(x) = x^2 \) est une fonction paire.

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Détermine si la fonction \( f(x) = x^3 \) est paire, impaire, ou ni l’un ni l’autre.

Voir la correction

– Vérifions la symétrie : \( f(-x) = (-x)^3 = -x^3 = -f(x) \). Donc, \( f(x) = x^3 \) est une fonction impaire.

👉🏻 Exercice 2 : Détermine si la fonction \( f(x) = \sin(x) \) est périodique, et si oui, trouve sa période.

Voir la correction

– La fonction \( f(x) = \sin(x) \) est périodique avec une période de \( 2\pi \), car \( \sin(x + 2\pi) = \sin(x) \) pour tout \( x \).

Méthode 8 : Asymptotes

1. Situation : Les asymptotes sont des lignes que le graphique d’une fonction approche de plus en plus près sans jamais les atteindre. Elles peuvent être verticales, horizontales, ou obliques et aident à comprendre le comportement limite d’une fonction.

2. Démarche à suivre :

1. Asymptotes verticales : Trouver les valeurs de \( x \) qui ne sont pas dans le domaine de la fonction, souvent là où le dénominateur d’une fonction rationnelle est égal à zéro.

2. Asymptotes horizontales : Analyser les limites de la fonction lorsque \( x \) approche l’infini positif ou négatif.

3. Asymptotes obliques : Si la fonction est une fraction rationnelle où le degré du numérateur est exactement un de plus que le degré du dénominateur, il y a une asymptote oblique. Effectuer la division de polynômes pour la trouver.

3. Pourquoi ça marche : Les asymptotes nous donnent des informations sur le comportement inférieur et supérieur des fonctions. Elles montrent comment la fonction se comporte à la limite, sans avoir besoin de calculer la fonction pour de grandes valeurs.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = \frac{1}{x-2} \). Trouve ses asymptotes.

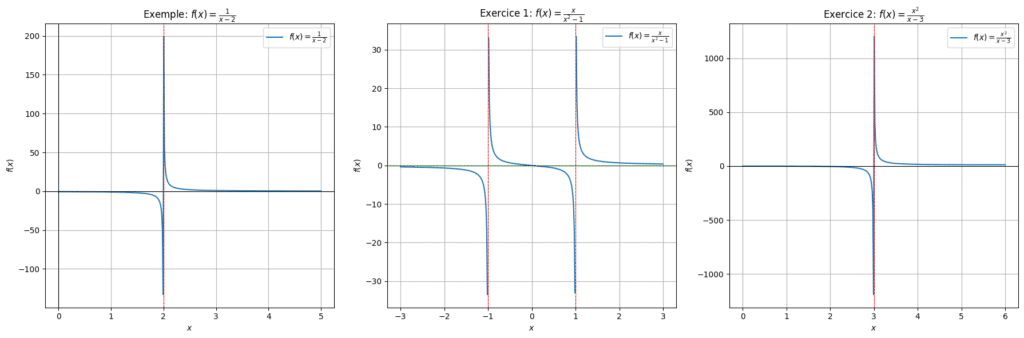
Correction :

1. Asymptote verticale : La fonction a une asymptote verticale à \( x = 2 \) car le dénominateur devient zéro lorsque \( x = 2 \).

2. Asymptote horizontale : Lorsque \( x \) approche l’infini, \( f(x) \) approche 0, donc il y a une asymptote horizontale à \( y = 0 \).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Trouve les asymptotes de la fonction \( f(x) = \frac{x}{x^2 – 1} \).

Voir la correction

– Asymptotes verticales : Les asymptotes verticales sont à \( x = -1 \) et \( x = 1 \) où le dénominateur est nul. – Asymptote horizontale : Lorsque \( x \) approche l’infini, \( f(x) \) approche 0, donc il y a une asymptote horizontale à \( y = 0 \).

👉🏻 Exercice 2 : Trouve les asymptotes de la fonction \( f(x) = \frac{x^2}{x-3} \).

Voir la correction

– Asymptote verticale : Il y a une asymptote verticale à \( x = 3 \). – Asymptote oblique : Puisque le degré du numérateur est un de plus que le degré du dénominateur, il y a une asymptote oblique. On peut trouver cette asymptote en effectuant une division polynomiale ou une division synthétique pour obtenir la ligne \( y = x + 3 \).

Méthode 9 : Concavité et points d’inflexion

1. Situation : La concavité d’une fonction décrit comment la courbe se courbe. Une fonction peut être concave vers le haut ou vers le bas, et les points d’inflexion sont les points où la concavité change. Ces concepts sont importants pour comprendre la forme globale d’une fonction.

2. Démarche à suivre :

1. Calculer la dérivée seconde : Trouver la dérivée seconde de la fonction pour étudier la concavité.

2. Étudier le signe de la dérivée seconde :

• Si \( f”(x) > 0 \), la fonction est concave vers le haut.
• Si \( f”(x) < 0 \), la fonction est concave vers le bas.

3. Trouver les points d’inflexion : Résoudre \( f”(x) = 0 \) pour trouver les points où la concavité change.

3. Pourquoi ça marche : La dérivée seconde d’une fonction donne des informations sur la courbure de la fonction. Un changement de signe de la dérivée seconde indique un point d’inflexion, où la courbure passe de concave vers le haut à concave vers le bas, ou vice versa.

4. Exemple d’application avec exercice corrigé :

Considère la fonction \( f(x) = x^3 – 3x^2 + 4 \). Étudie sa concavité et trouve ses points d’inflexion.

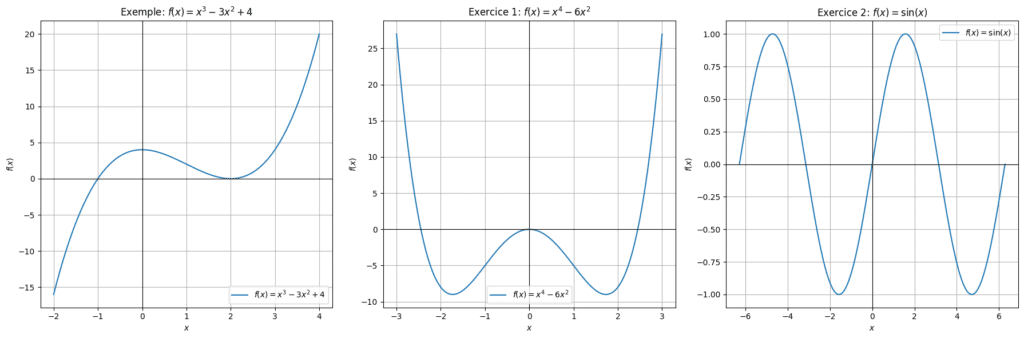
Correction :

1. Calculer la dérivée seconde : La dérivée première est \( f'(x) = 3x^2 – 6x \), et la dérivée seconde est \( f”(x) = 6x – 6 \).

2. Étudier le signe de la dérivée seconde :

• Pour \( x < 1 \), testons \( x = 0 \): \( f”(0) = -6 \) (concave vers le bas).
• Pour \( x > 1 \), testons \( x = 2 \): \( f”(2) = 6 \) (concave vers le haut).

3. Trouver les points d’inflexion : Résoudre \( 6x – 6 = 0 \) donne \( x = 1 \). Donc, il y a un point d’inflexion à \( x = 1 \).

5. Exercices supplémentaires :

👉🏻 Exercice 1 : Étudie la concavité de la fonction \( f(x) = x^4 – 6x^2 \) et trouve ses points d’inflexion.

Voir la correction

1. Calculer la dérivée seconde : \( f'(x) = 4x^3 – 12x \) et \( f”(x) = 12x^2 – 12 \). 2. Étudier le signe de la dérivée seconde : – Pour \( x 1 \), \( f”(x) > 0 \) (concave vers le haut). – Pour \( -1 < x < 1 \), \( f''(x) < 0 \) (concave vers le bas). 3. Trouver les points d'inflexion : Résoudre \( 12x^2 – 12 = 0 \) donne \( x = \pm 1 \). Donc, les points d'inflexion sont à \( x = -1 \) et \( x = 1 \).

👉🏻 Exercice 2 : Étudie la concavité de la fonction \( f(x) = \sin(x) \) et trouve ses points d’inflexion.

Voir la correction

1. Calculer la dérivée seconde : \( f'(x) = \cos(x) \) et \( f”(x) = -\sin(x) \). 2. Étudier le signe de la dérivée seconde : – La fonction \( \sin(x) \) change de signe périodiquement, donc la concavité change également périodiquement. 3. Trouver les points d’inflexion : Les points d’inflexion se produisent à chaque \( x = n\pi \) où \( n \) est un entier, car \( \sin(x) = 0 \) à ces points.