Calcul d’intégrales : méthode complète, formules et exemples

Le calcul d’intégrales, quelle plaie ! Tu as eu du mal à apprendre par coeur toutes les formules de dérivation et les domaines de dérivabilité. Tu pensais enfin en avoir fini avec tout cela et là ton prof de maths, te dit que tu vas attaquer un nouveau chapitre l’intégration… C’est reparti. Il faut tout réapprendre dans l’autre sens, car oui intégrer une fonction c’est plus ou moins l’inverse de la dériver. Il va donc falloir recommencer à apprendre des formules par coeur. Pour toutes les fonctions usuelles il te faudra connaitre les primitives usuelles et les domaines d’intégration. Il faudra aussi maîtriser les propriétés de l’intégrale et les astuces de calcul. Cette fiche de révision sur le calcul d’intégrales en terminale t’explique pas à pas les méthodes à connaître pour le bac.

Les formules à connaître pour le calcul d’intégrales en terminale

En terminale, le calcul d’intégrales permet notamment de déterminer des aires sous une courbe ou de résoudre certains problèmes en physique (distance à partir d’une vitesse par exemple).

Pour réussir, il est indispensable de connaître les primitives usuelles. Dans cette fiche complète, tu trouveras les méthodes essentielles pour calculer une intégrale définie ou indéfinie efficacement. Voici, pour commencer, un tableau pour te rafraîchir la mémoire.

$$\begin{array}{|c|c|c|}
\hline \text { Fonction } & \text { Primitive } & \text { Intervalle } \\
\hline f(x)=a & F(x)=a x & \mathrm{R} \\
\hline f(x)=x & F(x)=\frac{x^{2}}{2} & \mathrm{R} \\
\hline f(x)=x^{n} & F(x)=\frac{x^{n+1}}{n+1} & \mathrm{R} \\
\hline f(x)=\frac{1}{x} & F(x)=\ln x & ]0 ;+\infty[ \\
\hline f(x)=\frac{1}{x^{n}} \quad n \neq 1 & F(x)=-\frac{1}{(n-1) x^{n-1}} & ]-\infty ; 0[\text { ou }] 0 ;+\infty[ \\
\hline f(x)=\frac{1}{\sqrt{x}} & F(x)= 2 \sqrt{x} & ]0 ;+\infty[ \\
\hline f(x)=\sin x & F(x)=-\cos x & \mathrm{R} \\
\hline f(x)=\cos x & F(x)= \sin x & \mathrm{R} \\
\hline f(x)=e^{x} & F(x)=e^{x} & \mathrm{R} \\
\hline
\end{array}$$

Pour les intégrales les plus simples, il suffit de se rapporter à ce tableau en utilisant la linéarité de l’intégrale.

Quelques primitives usuelles à connaître en plus

Comment calculer une intégrale définie en terminale

Pour calculer une intégrale définie, on utilise la formule suivante :

$$\int_a^b f(x)\,dx = F(b) – F(a)$$

où F est une primitive de f.

Autrement dit : on trouve une primitive, puis on calcule sa valeur aux bornes.

Méthode 1 : utiliser la linéarité de l’intégrale

On peut séparer une somme :

$$\int (f(x)+g(x))dx = \int f(x)dx + \int g(x)dx$$

Exemple

$$\int_0^2 (3x^2 + 2)\,dx$$

On sépare :$$= 3\int_0^2 x^2 dx + 2\int_0^2 1 dx$$

Ainsi :

On calcule :$$= 12$$

Exemple détaillé

Calculer :$$\int_1^3 (2x^3 – x)\,dx$$

On sépare :$$= \int_1^3 2x^3 dx – \int_1^3 x dx$$

Ainsi

On utilise les primitives :$$= 36$$

Faire apparaître une fraction de la forme \(\frac{u’}{u}\)

C’est l’une des astuces à laquelle il faut penser ! Pour rappel, si u est une fonction à valeurs positives, alors \((ln(u))’=\frac{u’}{u}\). Cette formule est donc très utile pour le calcul d’intégrales, puisqu’elle permet d’intégrer des fractions !

Par exemple : imaginons que l’on veuille calculer \(\int_{0}^{2} \frac{x}{x^2+1} \, \mathrm{d}x\). On remarque que la dérivée de \(f(x)=x^2+1\) est \(f(x)=2x\). Il faut donc faire apparaitre \(2x\) au numérateur :

$$\begin{array}{ll}
\int_{0}^{2} \frac{x}{x^2+1} \, \mathrm{d}x & = \frac{1}{2} \int_{0}^{2} \frac{2x}{x^2+1} \, \mathrm{d}x \\
& = \frac{1}{2} [ln(x^2+1)]_0^2 \\
& = \frac{1}{2} (ln(2^2+1)-ln(0^2+1))\\
& = \frac{1}{2} (ln(5)-ln(1))\\
& = \frac{ln(5)}{2}
\end{array}$$

Vérifier ses résultats

Quand tu fais des exercices sur les intégrales n’hésite pas à te rendre sur le site wolfram alpha pour vérifier tes calculs. L’utilisation du logiciel de calcul est gratuit et te permet également de visualiser la fonction que tu intègres. C’est très utile pour le calcul d’intégrales.

Faire apparaître une fonction de la forme \(u’e^{u}\)

Tableau des primitives usuelles (avec $u(x)$)

Comment lire ce tableau ?

Si tu reconnais dans une intégrale :

• une fonction $u(x)$,
• multipliée par sa dérivée $u'(x)$,

alors tu peux appliquer directement la ligne correspondante.

Exemple rapide

$$\int (3x^2)\,e^{x^3}\,dx$$

Ici :$$u(x)=x^3 \quad \Rightarrow \quad u'(x)=3x^2$$

On est dans la ligne :$$u'(x)e^{u(x)}$$

Donc la primitive est :$$e^{x^3} + C$$

La méthode du changement de variable

Dans beaucoup de cas, les astuces vues précédemment correspondent en réalité à une méthode plus générale appelée changement de variable.

L’idée est simple :
Si une intégrale contient une expression du type $f(g(x))\,g'(x)$, on pose :

Cela permet de transformer l’intégrale en une forme plus simple.

Par exemple, dans :

On peut poser :

Et

Ainsi, on fait apparaître u’ (la dérivée de u, notée également du) :

On transforme les bornes avec x=0

et avec x=1

Ainsi, l’intégrale devient donc :

On calcule donc :

Si l’astuce marche avec la fonction logarithme, elle marche aussi avec la fonction exponentielle !

Exemple avec changement de variable

Calculer :$$\int_{0}^{1} (2x+1)e^{x^2+x}\,dx$$

On pose :$$u = x^2 + x$$

Alors :$$u’ = 2x+1$$

On reconnaît la forme :$$u’e^u$$

Donc :$$= [e^{x^2+x}]_0^1$$$$= e^2 – 1$$

En effet, la dérivée de la fonction du type \(e^{u}\) est \((e^{u})’=u’e^{u}\). Une astuce très utile dans le calcul d’intégrales.

Exemple si on veut calculer \(\int_{0}^{1} x^2e^{x^3+4} \, \mathrm{d}x\). On remarque que la dérivée de \(f(x)=x^3+4\) est \(f(x)=3x^2\). Il faut donc faire apparaitre \(3x^2\) :

$$\begin{array}{ll}
\int_{0}^{1} x^2e^{x^3+4} \, \mathrm{d}x & = \frac{1}{3} \int_{0}^{1} 3x^2e^{x^3+4} \, \mathrm{d}x \\
& = \frac{1}{3} [e^{x^3+4}]_0^1 \\
& = \frac{1}{3} (e^{1^3+4}-e^{0^3+4})\\
& = \frac{1}{3} (e^5-e^4)
\end{array}$$

Utiliser la parité ou l’imparité d’une fonction

Pourquoi s’embêter avec le calcul d’intégrales quand on peut appliquer directement un résultat de cours !

Par exemple, si on veut calculer \(\int_{-1}^{1} x^3+4 \, \mathrm{d}x\), comment fait-on? Et bien on peut appliquer la méthode 1, on utilise la linéarité de l’intégrale et on écrit \(\int_{-1}^{1} x^3+4x \, \mathrm{d}x= \int_{-1}^{1} x^3 \, \mathrm{d}x + 4 \int_{-1}^{1} x\, \mathrm{d}x\), et on calcule en utilisant le tableau des primitives usuelles.

Mais on peut aller beaucoup plus vite, si on considère la fonction f définie par \(f(x)=x^3+4x\), alors on remarque que \(f(-x)=(-x)^3+4(-x)=-(x^3+4x)=-f(x)\).

La fonction $f$ est donc impaire et on sait par théorème que l’intégrale que l’on cherche à calculer est nulle. On laissera au lecteur le soin de le vérifier en terminant le calcul.

Cela se voit très bien graphiquement :

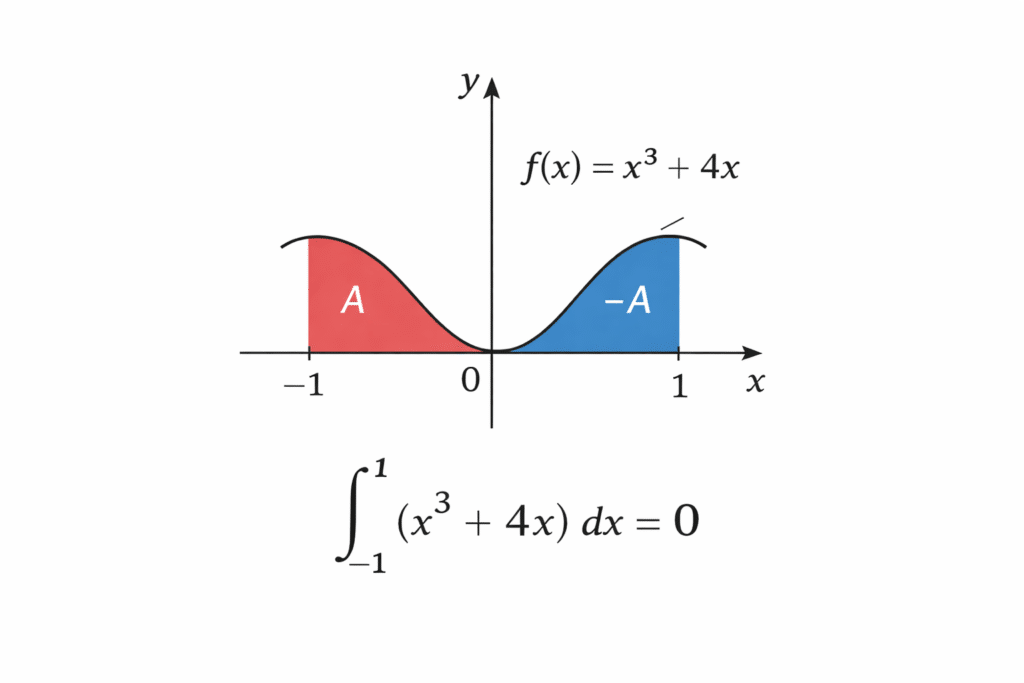
Si on considère maintenant \(\int_{-1}^{1} x^2+4 \, \mathrm{d}x\), alors en considérant la fonction \(f(x)=x^2+4\) on remarque que la fonction $f$ est paire c’est à dire que \(f(-x)=f(x)\).

Cela se voit très bien en regardant la courbe de la fonction :

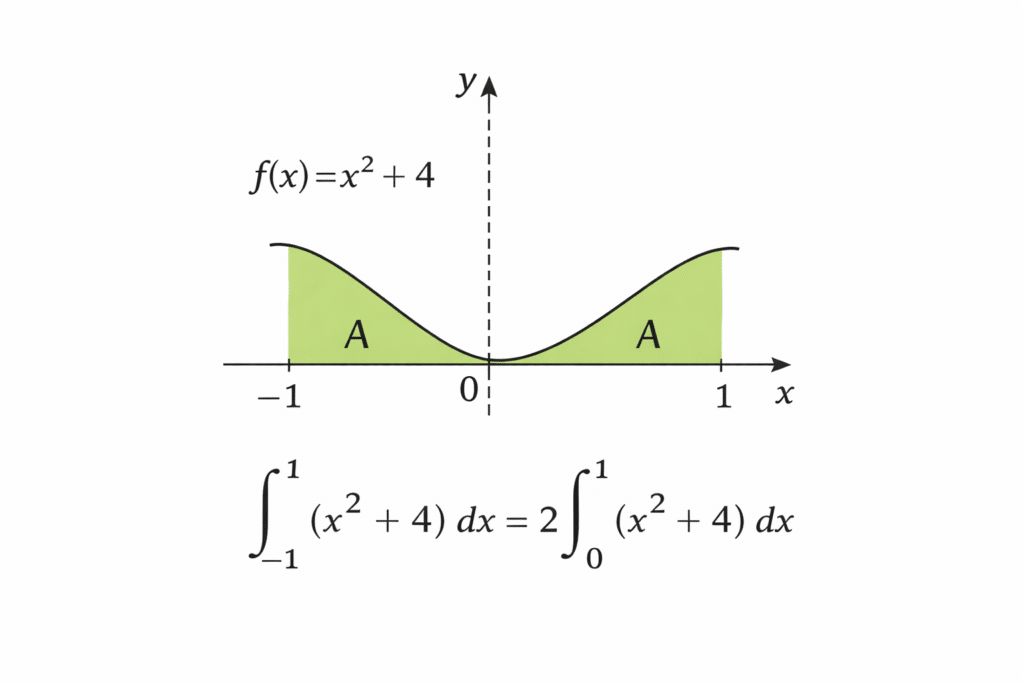
Par théorème on sait que l’intégrale vaut \(\int_{-1}^{1} x^2+4 \, \mathrm{d}x = 2 \int_{0}^{1} x^2+4 \, \mathrm{d}x \). Il ne reste qu’à calculer en appliquant la méthode 1 :

$$\begin{array}{ll}
\int_{-1}^{1} x^2+4 \, \mathrm{d}x & = 2 \int_{0}^{1} x^2+4 \, \mathrm{d}x \\
& = 2(\frac{1}{3} [x^3]_0^1+4[x]_0^1) \\
& = 2 (\frac{1}{3} +4)\\
& = \frac{26}{3}
\end{array}$$

Les erreurs fréquentes dans le calcul d’intégrales

Voici les pièges les plus courants :

• Oublier d’appliquer F(b) − F(a) correctement
• Oublier les parenthèses lors de l’évaluation aux bornes
• Confondre primitive et intégrale définie
• Oublier la constante dans le cas d’une primitive (intégrale indéfinie)
• Se tromper sur le domaine (ex : ln(x) définie seulement pour x > 0)

Pourquoi apprend-on le calcul d’intégrales ?

En mathématiques, une intégrale définie permet de calculer l’aire sous la courbe, les applications sont nombreuses :

• La distance parcourue à partir d’une vitesse
• Une probabilité en loi continue
• Un volume en physique

Par exemple, si une fonction $f$ est positive sur l’intervalle $[a ; b]$, alors l’intégrale

$$\int_a^b f(x)\,dx$$

représente l’aire comprise entre la courbe de $f$, l’axe des abscisses et les droites d’équation $x=a$ et $x=b$.

Points clés à retenir sur le calcul d’intégrales

• Une intégrale définie se calcule avec la formule :

$$\int_a^b f(x)\,dx = F(b) – F(a)$$

où $F$ est une primitive de $f$.

• Il faut connaître les primitives usuelles : puissances, exponentielle, sinus, cosinus, $\frac{1}{x}$, etc.

• La linéarité permet de séparer une somme :

$$\int (f+g) = \int f + \int g$$

• Si on reconnaît une forme $\frac{u’}{u}$, on pense au logarithme.

• Si on reconnaît une forme $u’e^u$, on peut utiliser un changement de variable.

• Si la fonction est impaire, l’intégrale sur $[-a;a]$[−a;a] vaut 0.
• Si la fonction est paire, on peut écrire :

$$\int_{-a}^{a} f(x)\,dx = 2\int_{0}^{a} f(x)\,dx$$

• Attention aux erreurs fréquentes : oublier $F(b)-F(a)$, oublier les parenthèses ou la constante $C$ pour une primitive.

Voilà qui conclut cette fiche complète sur le calcul d’intégrales. Avec ces méthodes (primitives usuelles, linéarité, changement de variable, parité et astuces logarithme/exponentielle), tu disposes de toutes les techniques indispensables pour réussir tes exercices d’intégration au lycée. N’hésite pas à t’entraîner sur nos annales pour mettre en application tout ce que tu viens d’apprendre !

FAQ : Calcul d’intégrales : méthode complète, formules et exemples