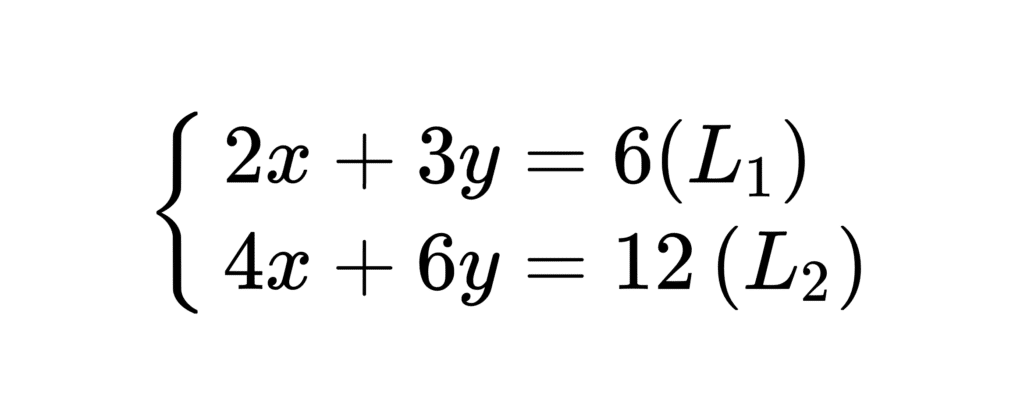Tu as déjà résolu des équations, mais que faire quand il y en a plusieurs à résoudre en même temps ? C’est là qu’interviennent les systèmes d’équations linéaires, un concept clé de la seconde au baccalauréat… et au-delà ! Que ce soit pour modéliser un problème ou réussir tes exercices, maîtriser ces systèmes est essentiel. Pour les résoudre, deux méthodes incontournables : la substitution et les combinaisons linéaires. À la fin, tu sauras identifier et résoudre tous types de systèmes : avec une solution unique, aucune ou une infinité. Prêt(e) à devenir un pro des équations ? C’est parti !
Méthode de substitution pour résoudre des systèmes d’équations linéaires
Cette méthode consiste à exprimer l’une des inconnues en fonction de l’autre à partir d’une équation, puis à remplacer cette expression dans la seconde équation. Cela permet d’obtenir une équation à une seule variable, qu’on peut alors résoudre facilement. Une fois la première variable trouvée, on la remplace dans l’équation initiale pour obtenir la seconde variable.
👉🏻 Exemple :
Résolvons le système suivant : \begin{cases} y = 5 – x \\ 2x – y = 1 \end{cases}
- Remplaçons \( y \) dans la seconde équation : \(\begin{cases} y = 5 – x \\ 2x – (5 – x) = 1 \end{cases} \)
- Simplifions : \( \begin{cases} y = 5 – x \\ 3x = 6 \end{cases} \)
- Résolvons pour \( x \) : \( \begin{cases} y = 5 – x \\ x = 2 \end{cases} \)
- Trouvons \( y \) : \( \begin{cases} y = 5 – 2 = 3 \\ x = 2 \end{cases} \)
👉🏻 Solution : \( (x, y) = (2,3)\)
Méthode des combinaisons linéaires pour résoudre des systèmes d’équations linéaires
Cette méthode consiste à additionner ou soustraire les équations d’un système afin d’éliminer une inconnue et d’obtenir une équation plus simple. Cela permet de résoudre progressivement le système en trouvant les valeurs des variables une par une.
👉🏻 Exemple 1 : Addition des équations
Résolvons le système : \( \begin{cases} 3x + 2y = 11 \\ 5x – 2y = 9 \end{cases} \)
Additionnons les deux équations : \( \begin{cases} (3x+2y)+(5x−2y)=11+9(3x + 2y) + (5x – 2y) = 11 + 9 \\ 5x – 2y = 9 \end{cases} \)
Simplifions : \( \begin{cases} 8x = 20 \\ 5x – 2y = 9 \end{cases} \)
Résolvons pour \( x \) : \( \begin{cases} x= \frac{20}{8}=2.5 \\ 5x – 2y = 9 \end{cases} \)
Remplaçons \( x \) dans la deuxième équation : \( \begin{cases} x= 2.5 \\ 5 \times 2.5 – 2y = 9 \end{cases} \)
Isolons \( y \) : \( \begin{cases} x= 2.5 \\ y = \frac{-3,5}{-2} = 1,75 \end{cases} \)
La solution du système est donc : \( (x,y) = (2.5, 1.75) \)
👉🏻 Exemple 2 : Soustraction des équations
Résolvons le système : \begin{cases} 4x + 3y = 18 \\ 2x + 3y = 10 \end{cases}
Soustrayons la seconde équation de la première : \begin{cases} (4x+3y)−(2x+3y)=18−10 \\ 2x + 3y = 10 \end{cases}
Simplifions : \begin{cases} 2x = 8 \\ 2x + 3y = 10 \end{cases}
- Résolvons pour \( x \) : \begin{cases} x = \frac{8}{2} = 4 \\ 2x + 3y = 10 \end{cases}
- Remplaçons \( x \) dans la seconde équation : \begin{cases} x = 4 \\ 2 \times 4 + 3y = 10 \end{cases}
- Trouvons \( y \) : \begin{cases} x = 4 \\ y = \frac{10 – 8}{3} = \frac{2}{3} \end{cases}
👉🏻 Solution : \( (x, y) = (4, \frac{2}{3}) \)
Les solutions des systèmes d’équations linéaires
Dans les exemples précédents, nous avons vu comment résoudre un système de deux équations à deux inconnues en utilisant la méthode de substitution et la méthode des combinaisons linéaires. Nous avons trouvé des solutions uniques sous la forme d’un couple \( (x,y) \). Toutefois, il est important de noter qu’un système peut avoir différents types de solutions.
Systèmes d’équations linéaires avec une solution unique
Les systèmes d’équations que nous avons résolus précédemment avaient une solution unique, c’est-à-dire un seul couple\( (x,y) \) satisfaisant simultanément les deux équations. Cela correspond à deux droites sécantes (qui se coupent en un unique point).
En notation algébrique, si un système de deux équations linéaires est de la forme : \begin{cases} a_1x+b_1y = c_1 \\ a_2x+b_2y=c_2 \end{cases}
Alors il admet une solution unique si les coefficients ne sont pas proportionnels, c’est-à-dire si : \( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)
👉🏻 Exemple : \( \begin{cases} 3x + 2y = 11 \\ 5x – 2y = 9 \end{cases} \)
Nous avons trouvé la solution \( (x,y) = (2.5 , 3) \), ce qui signifie que ces deux équations se croisent en un point unique dans le plan cartésien.
Systèmes d’équations linéaires sans solution (système incompatible)
Un système d’équations linéaires n’a pas de solution lorsqu’il est incompatible, c’est-à-dire lorsque les équations représentent deux droites parallèles qui ne se croisent jamais. Cela se produit lorsque les coefficients des variables sont proportionnels (c’est-à-dire que les droites ont la même pente), mais que les termes constants ne respectent pas cette même proportionnalité.
En notation algébrique, si un système de deux équations linéaires est de la forme : \begin{cases} a_1x+b_1y = c_1 \\ a_2x+b_2y=c_2 \end{cases}
Alors il est sans solution si : \( \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} \)
Cela signifie que les droites ont la même pente mais des ordonnées à l’origine différentes, donc elles sont parallèles et ne se coupent jamais.
👉🏻 Exemple : \begin{cases} x + y = 2 \\ x + y = 5 \end{cases}
Ici, une même somme \( x + y \) donne deux résultats différents, ce qui est impossible. Le système est incompatible.
Ainsi \( S = \emptyset \)
Systèmes d’équations linéaires avec une infinité de solutions
Un système d’équations a une infinité de solutions lorsque ses équations sont proportionnelles, c’est-à-dire lorsqu’elles représentent la même droite dans un repère.
Un système a une infinité de solutions si les coefficients des variables et les constantes sont proportionnels : \( \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} \)
👉🏻 Exemple : \begin{cases} 2x+3y=6 (L_1) \\ 4x+6y=12 (L_2) \end{cases}
On remarque que la seconde équation est le double de la première. Cela signifie que ces deux équations sont équivalentes et décrivent la même droite.
Le système possède une infinité de solutions, car toutes les solutions de la première équation sont aussi solutions de la seconde.
Posons \( y=t \) (paramètre réel), alors : \( \begin{cases} x = \frac{6 – 3t}{2} \\ y = t , \quad t \in \mathbb{R} \end{cases} \)
Ainsi : \( S = \left\{ \left(\frac{6 – 3t}{2}, t \right) \mid t \in \mathbb{R} \right\} \)
Maintenant que tu connais l’essentiel, tu es prêt(e) à aborder le bac avec confiance et maîtrise des systèmes d’équations linéaires !