Si tu galères parfois à comprendre une consigne complexe en maths, cet article est fait pour toi ! Les consignes, on les retrouve partout, que ce soit en algèbre, en géométrie ou même en probabilités. Au lycée, et surtout pour le bac, savoir bien décoder une consigne peut faire toute la différence pour éviter les erreurs et gagner du temps. Ici, je vais t’aider à y voir plus clair, à déchiffrer les questions compliquées et à te sentir plus confiant quand tu bosses tes exercices. Prêt à devenir un pro du décodage ? C’est parti !
Comprendre ce qui est demandé en maths
Décomposer la consigne
Imagine qu’on te donne cette consigne : « Déterminer la solution de l’équation suivante : \( x^2 = 9 \) ». C’est basique, mais parfait pour capter l’idée ! Avant de foncer dans les calculs, il faut bien saisir ce que la consigne demande vraiment — et ça commence avec le repérage des mots importants.
Démarche
Première étape : repérer les verbes d’action comme « déterminer », « prouver », « calculer », etc. Ils te disent ce que tu dois faire (calcul, démonstration, interprétation…). Par exemple, « Déterminer » indique que le prof attend un résultat, souvent sans forcément toute la justification.
Ensuite, identifie les objets mathématiques concernés : s’agit-il d’une équation, d’un vecteur, d’une fonction, d’un tableau de valeurs ? Dans notre exemple : tu travailles avec une équation.
Enfin, délimite précisément ce qui est demandé. Ici, on cherche la solution exacte, pas forcément une interprétation ou un graphique.
Mini-exercice
Exercice 1
À partir de la consigne « Démontrer que la droite \( d \) d’équation \( y = 2x + 1 \) passe par le point A(1,3) », repère :
– Le verbe d’action
– L’objet mathématique sur lequel tu travailles
– L’objectif de la consigne
Voir la correction
– Verbe d’action : « Démontrer » = il faut prouver.– Objet maths : la droite \( y = 2x + 1 \), le point A(1,3)
– Objectif : montrer que le point A appartient à la droite, donc vérifier que les coordonnées de A vérifient l’équation.
Analyser le contexte mathématique
Imagine maintenant que tu dois résoudre : « Étudier les variations de la fonction \( f(x) = -x^2 + 4x – 1 \) sur \( [0;5] \) ». Avant de t’y plonger, il faut savoir dans quel chapitre tu te trouves, pour sortir les bons outils.
Démarche
1. Définir le domaine : repère si tu es en algèbre, analyse, géométrie, statistiques, etc. Cela t’aide à anticiper quelle méthode tu vas employer.
2. Identifier le type d’exercice : résolution d’équations, étude de signes, représentation graphique… Ici, c’est l’étude de fonction et de ses variations.
3. Relier aux notions et chapitres du programme : est-ce un contenu déjà vu, ou plutôt une nouveauté ? Ici, tu utilises les connaissances sur les fonctions du second degré.
Exemple d’application
Exercice 2
Consigne : « Trouver les solutions de l’équation \( 2x – 3 = 7 \) et représenter ces solutions sur un axe gradué. »
Voir la correction
– Domaine : algèbre– Type d’exercice : résolution d’équation du premier degré + représentation graphique.
– Solution : \( 2x – 3 = 7 donc 2x = 10 donc x = 5 \)
Reformulation et schématisation
Ce dernier point est la clé pour éviter de s’emmêler les pinceaux ! Supposons la consigne : « Soit le triangle ABC tel que AB = 3, AC = 4 et l’angle BAC = 90°. Calculer la longueur BC. »
Démarche
1. Reformule la consigne avec tes mots : « On me donne un triangle rectangle avec deux côtés connus ; il faut trouver le troisième. »
2. Liste les données connues/inconnues :
Connues : AB = 3, AC = 4, angle BAC = 90°
Inconnue : BC ?
3. Fais un schéma, un tableau ou une illustration numérique pour bien visualiser la situation (ça évite pas mal d’erreurs !).
Exemple d’application
Exercice 3
Consigne : « On considère la fonction \( f(x) = x^2 – 4x + 3 \). Représenter graphiquement la fonction sur l’intervalle [0 ; 5] et donner les solutions de l’équation \( f(x) = 0 \). »
Voir la correction
– Connues : expression de la fonction, l’intervalle pour x.– Inconnues : les zéros de la fonction et la courbe.
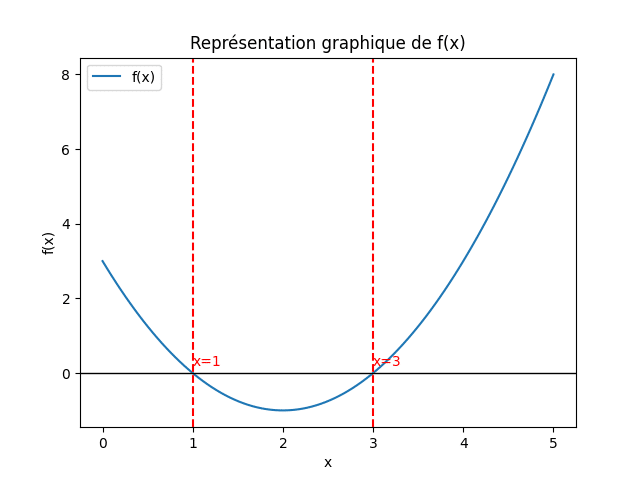
– Les solutions de \( x^2 – 4x + 3 = 0 \) sont \( x = 1 \) et \( x = 3 \).
– Schéma : courbe parabolique qui coupe l’axe des abscisses en 1 et 3.
Entraîne-toi ! Exercices corrigés
Exercice 4
Décompose la consigne suivante : « Déterminer l’ensemble des solutions de l’inéquation \( 3x + 2 > 11 \). »
Voir la correction
– Verbe d’action : Déterminer – Objet mathématique : inéquation du premier degré – Objectif : trouver tous les x tels que \( 3x + 2 > 11 \), soit \( x > 3 \). Représente la solution à l’aide d’un segment ouvert à partir de x = 3.Exercice 5
Dans la consigne : « Justifier que le vecteur \( \vec{u} = (2,1) \) est normal à la droite d’équation \( x – 2y + 3 = 0 \). »
Voir la correction
– Verbe : Justifier = expliquer.– Objet : vecteur, droite.
– Objectif : montrer que le vecteur est normal à la droite.
– Rappel : un vecteur normal à une droite d’équation \( ax + by + c = 0 \) a pour coordonnées \( (a, b) \).
Donc pour la droite \( x – 2y + 3 = 0 \), un vecteur normal est \( (1, -2) \). Le vecteur \( (2,1) \) n’est pas normal mais pourrait être testé en calculant un produit scalaire ou en le comparant.
Identifier la méthode de résolution à employer
Rassembler les outils et théorèmes pertinents
Ok, imaginons que tu dois démontrer que deux droites sont parallèles. Première chose à faire : lister dans ta tête (ou sur ton brouillon !) tout ce qui peut te servir. Genre, « deux droites sont parallèles si elles ont le même coefficient directeur », ou « deux vecteurs directeurs colinéaires »… Tu vois le délire ?
L’idée, c’est de regrouper tous les outils, propriétés et théorèmes qui sont compatibles avec la question et avec les données. Avant de foncer, vérifie que chaque théorème s’applique bien (exemple : la dérivée d’une fonction, attention à son domaine !), et n’oublie pas les définitions officielles du cours — ça peut sauver la mise en rédaction.
Exercice 2
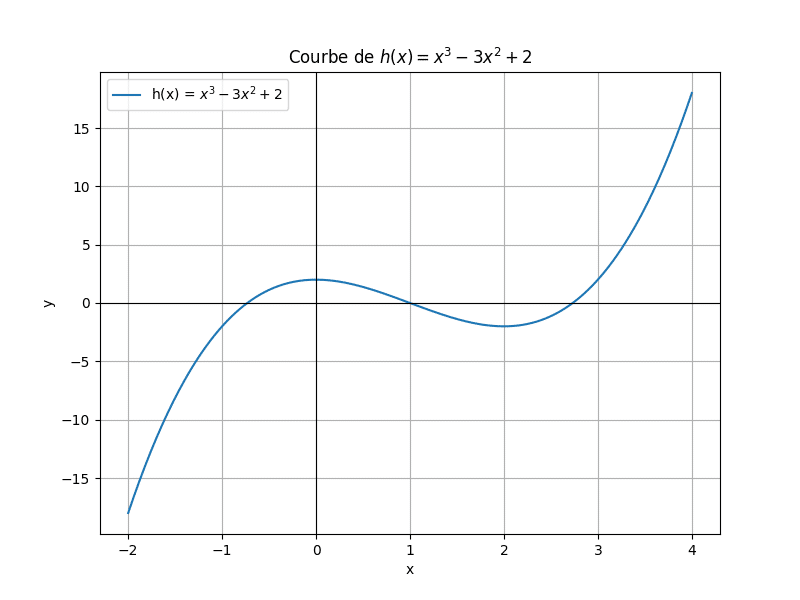
Voici la question : « Étudier les variations de ((h(x) = x^3 – 3x^2 + 2)) ». No stress, commence par lister les outils nécessaires avant de démarrer le calcul !
Voir la correction
- Formule de la dérivée : ((h'(x)))
- Recherche des racines de la dérivée pour les extremums
- Signe de la dérivée pour les variations
- Tableau de variations
Graphique pour l’exercice 2
Élaborer un plan de résolution
Supposons qu’on te demande « Résoudre ((x^2-5x+6=0)) ». Plutôt que d’improviser, découpe toujours ta résolution en étapes bien claires :
- Chercher une méthode adaptée : ici, méthode du discriminant pour les équations de degré 2.
- Calculer le discriminant ((\Delta)).
- Trouver les solutions en appliquant la formule magique.
- Vérifier si les solutions sont bien dans l’ensemble de définition (pour les équations rationnelles, par exemple).
N’hésite jamais à écrire ces étapes sur ton brouillon, même si ça te paraît simple. Et, à la fin, relis-toi avec un œil critique : ça colle partout, tu n’as rien oublié, tout est cohérent ?
Exercice 3
Résous ((x^2-5x+6=0)) en détaillant ton plan de résolution puis vérifie tes solutions.
Voir la correction
- Reconnaissance : équation du second degré → discriminant.
- ((\Delta = (-5)^2 – 4 \times 1 \times 6 = 25 – 24 = 1))
- Deux solutions réelles distinctes car ((\Delta > 0)) :
- ((x_1 = \frac{5 – \sqrt{1}}{2} = 2)), ((x_2 = \frac{5 + \sqrt{1}}{2} = 3))
- Vérification rapide : ((2^2 – 5 \times 2 + 6 = 4 – 10 + 6 = 0)), idem pour 3.
Graphique pour l’exercice 3
Pour représenter la fonction ((x^2-5x+6)), qui s’annule précisément pour les solutions trouvées ci-dessus, tu peux tracer la courbe et voir les points d’intersection avec l’axe des abscisses. Voici le code Python associé :
Exercice 4
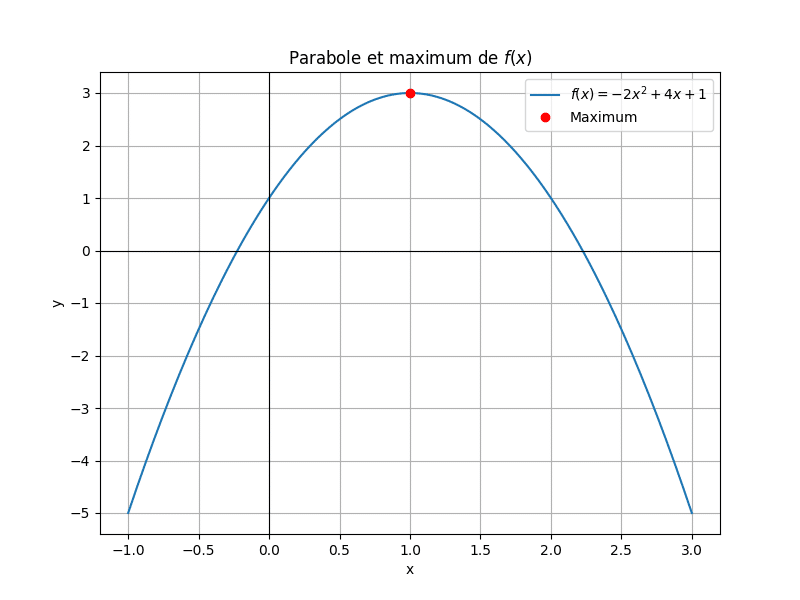
Voici un énoncé type bac : « On considère la fonction ((f(x) = -2x^2 + 4x + 1)). Étudie ses variations et donne le maximum. » Applique une démarche étape par étape.
Voir la correction
- Dériver : ((f'(x) = -4x + 4))
- Recherche du signe de ((f« (x))) pour les extrémums : ((f »(x)=0)) pour ((x=1)).
- Tableau de variations :
– Avant 1, dérivée positive : fonction croissante.
– Après 1, dérivée négative : fonction décroissante. - Donc maximum en ((x=1)) : ((f(1) = -2 + 4 + 1 = 3))
Pour le graphique :
Exercice 5
Pour l’équation ((\frac{x+3}{x-1}=2)), détaille toutes les étapes (détermination du domaine, résolution, vérification du cas interdit). Donne la solution.
Voir la correction
- Domaine : ((x\neq 1)) (car sinon le dénominateur s’annule).
- Résolution :
((\frac{x+3}{x-1}=2))
((x+3=2(x-1)))
((x+3=2x-2))
((3+2=2x-x))
((5=x)) - Vérification : ((x=1)) est interdit, mais ((x=5)) c’est bon.
- Solution : ((x=5)).
Bravo, tu vois qu’en découpant chaque exercice et en te fiant aux indices de l’énoncé, tu simplifies ta vie… et tu gagnes des points faciles ! La clé, c’est de toujours travailler en 3 temps : repérer la méthode, rassembler les outils et organiser ta résolution. Courage, l’entraînement paie toujours !
Exercices !
Identifier les verbes d’action et objets mathématiques dans une consigne
Tu t’es déjà retrouvé devant un énoncé du genre : « Montrer que la fonction \( (((f(x) = 2x + 3))) \) est strictement croissante sur \( (((\mathbb{R}))) \) » et tu t’es demandé par où commencer ? Eh bien, tout commence par le repérage des verbes d’action (ici, « Montrer ») et des objets mathématiques (ici, la fonction \( (((f))) \) et l’ensemble \( (((\mathbb{R}))) \)).
Le grand principe ici, c’est d’apprendre à mettre en lumière les attentes de la consigne pour ne pas partir dans le mauvais sens ! Quand tu lis un énoncé, surligne le ou les verbes d’action (« Exprimer », « Calculer », « Démontrer », « Justifier », etc.), puis repère l’objet de la demande (fonction, équation, vecteur…). Bref, survolez l’énoncé comme si tu cherchais les ingrédients d’une recette !
Exercice 1
Voici trois consignes. Pour chacune, souligne le ou les verbes d’action et encadre l’objet principal :
1. Calculer l’image de 5 par la fonction \( (((g(x) = x^2 – 4))) \).
2. Déterminer l’ensemble des solutions de l’équation \( (((x^2 – 3x + 2 = 0))) \).
3. Justifier que la droite \( (((d))) \) est parallèle à la droite \( (((\Delta))) \).
Voir la correction
- 1. Calculer (verbe d’action) ; Objet principal : l’image de 5 par \( (((g))) \).
- 2. Déterminer (verbe d’action) ; Objet principal : l’ensemble des solutions de l’équation \( (((x^2 – 3x + 2 = 0))) \).
- 3. Justifier (verbe d’action) ; Objet principal : la relation entre la droite \( (((d))) \) et la droite \( (((\Delta))) \).
Exercices guidés de planification
Construire un plan face à un problème
Quand tu lis une question difficile et que tu te sens perdu, c’est souvent que tu n’as pas de PLAN. L’idée ici : apprendre à tracer ta carte au trésor avant de chercher l’or !
Pour chaque problème, il est important de :
- Découper la question en étapes logiques.
- Associer chaque étape à une méthode connue (calcul, démonstration, schéma, etc.).
- Se poser la question : ai-je toutes les infos pour avancer ?
Exercice 2
Soit la fonction \( (((f(x) = x^2 – 2x + 1))) \). Formule un plan pour répondre à la question : Résoudre \( (((f(x) = 0))) \).
Voir la correction
- Étape 1 : Écrire l’équation : \( (((x^2 – 2x + 1 = 0))) \).
- Étape 2 : Chercher une factorisation éventuelle.
- Étape 3 : Résoudre l’équation factorisée ou utiliser la formule quadratique si nécessaire.
Exercice 3
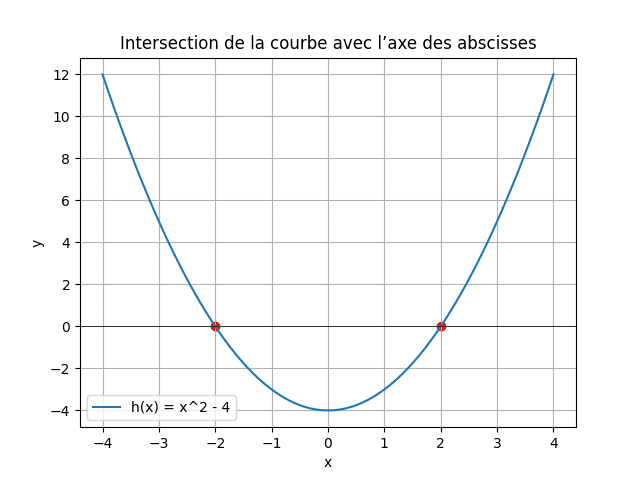
Problème : « Montrer graphiquement que la courbe de la fonction \( (((h(x) = x^2 – 4))) \) coupe l’axe des abscisses en deux points distincts. »
Voir la correction avec graphique
- Étape 1 : Dresser le tableau de signes ou factoriser : \( (((x^2 – 4 = (x-2)(x+2))) \).
- Étape 2 : Localiser les racines : \( (((x = -2))) \) et \( (((x = 2))) \).
- Étape 3 : Dessiner la courbe et l’axe \( (((y = 0))) \).
- Étape 4 : Vérifier graphiquement que la courbe coupe l’axe en ces deux points.
Problèmes complets type baccalauréat
Aller de l’énoncé à la solution complète
Bienvenue dans la cour des grands ! Ici, on mélange plusieurs compétences : lecture fine de la consigne, organisation, calcul, argumentation… et intuition graphique. On va s’entraîner sur des problèmes façon bac. Prends ton crayon, c’est parti !
Exercice 4
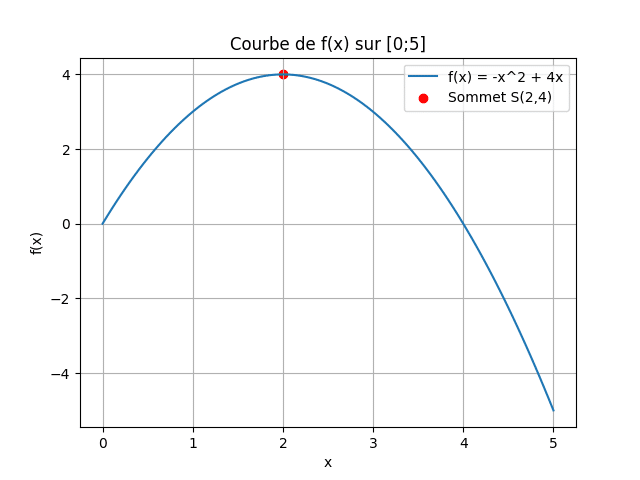
Soit la fonction \( (((f(x) = -x^2 + 4x))) \) définie sur \( ((([0; 5]))) \).
- 1. Calcule les coordonnées du sommet de la parabole.
- 2. Étudie les variations de \( (((f))) \).
- 3. Représente graphiquement \( (((f))) \) sur \( ((([0;5]))) \).
Voir la correction avec graphique Python
- Le sommet de \( (((f))) \) est à \( (((x_s = -b/2a = -4/(-2) = 2))) \), donc \( (((y_s = f(2) = -4 + 8 = 4))) \), sommet : \( (((S(2;4)))) \).
- Variations : – Pour \( (((x \leq 2))) \) : \( (((f))) \) croissante ; – Pour \( (((x \geq 2))) \) : \( (((f))) \) décroissante.
-
Graphique Python :
Exercice 5
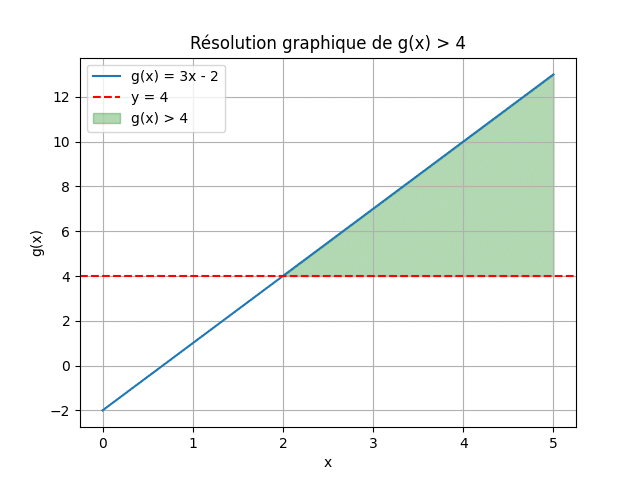
On considère la fonction \( (((g(x) = 3x – 2))) \). Résous, graphiquement puis algébriquement, l’inéquation \( (((g(x) > 4))) \).
Voir la correction avec graphique Python
- Algébrique : \( (((3x – 2 > 4))) \implies (((3x > 6))) \implies (((x > 2))) \).
- Graphique :
Tu peux maintenant attaquer sereinement tout exercice, du plus simple au casse-tête du bac, en sachant repérer, organiser et t’orienter pas à pas vers la solution. Plus tu t’entraînes, plus cette méthode deviendra naturelle. Courage ! 🚀