En analyse, l’étude des asymptotes permet de comprendre le comportement d’une fonction à l’infini ou au voisinage d’une valeur interdite. Savoir déterminer une asymptote horizontale, verticale ou oblique est une compétence essentielle en mathématiques au lycée, notamment pour l’étude des limites et l’interprétation des représentations graphiques. Dans cet article, tu découvriras ce qu’est une asymptote, comment l’identifier à l’aide des limites, et quelles méthodes utiliser pour analyser le comportement asymptotique d’une fonction, avec des explications claires et des exemples utiles pour le bac.
Définition – Qu’est-ce qu’une asymptote en mathématiques ?
En mathématiques, une asymptote est une droite vers laquelle la courbe représentative d’une fonction se rapproche de plus en plus lorsque la variable tend vers l’infini ou vers une valeur interdite, sans jamais l’atteindre. L’étude des asymptotes permet de décrire le comportement asymptotique d’une fonction, notamment grâce au calcul des limites, et de mieux comprendre la forme de sa représentation graphique.
Illustration et exemple de l’asymptote :
Soit \(D\) la droite d’équation \(y=ax+b\), et \(C_f\) la courbe d’équation \(y=f(x)\),
On dit que la droite \(D\) est asymptote à une courbe \(C_f\) en \(±\infty\) si la distance |\(f(x)-(ax+b)\)| entre la courbe \(C_f\) et la droite \(D\) tend vers \(0\) quand \(x\) tend vers \(±\infty\).
Trois cas particuliers – Asymptote
Asymptote oblique
Dire que la droite d’équation \(y=ax+b\) est asymptote à \(C_f\) en \(±\infty\) signifie qu’il est possible d’écrire \(f(x)=ax+b+g(x)\), où \(g\) est une fonction qui tend vers \(0\) quand \(x\) tend vers \(±\infty\).
Asymptote horizontale
Si \(a=0\), l’asymptote est parallèle à l’axe des abscisses.
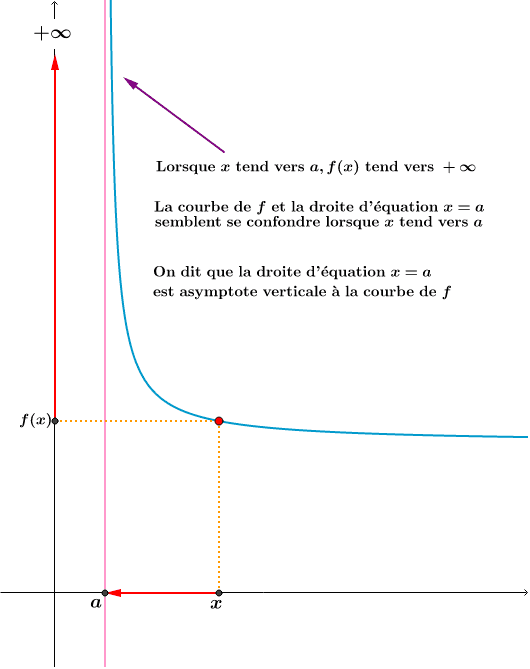
Asymptote verticale
On dit que la droite d’équation \(x=x_0\) est asymptote à \(C_f\) si, et seulement si,
- \(\lim \limits_{x \to x_0}f(x)=±\infty\),
- Ou si \(\lim \limits_{x \to x_0^+}f(x)=±\infty\),
- Ou encore si \(\lim \limits_{x \to x_0^-}f(x)=±\infty\)
L’asymptote est alors parallèle à l’axe des ordonnées.
Asymptotes en \(-\infty\), en \(+\infty\) et en \(x_0\)
Quand \(x\) tend vers \(±\infty\), on distingue trois cas :
- Si la limite de \(f\) est infinie, il est possible que \(C_f\) ait une asymptote oblique
\(\:\)
Attention : ce n’est pas certain.
On pourra utiliser comme contre-exemple la fonction \(f(x)=x^2\).
\(\:\) - Si la limite est finie (i.e. si \(l\) est la limite, où \(l \in \mathbb{R}\)), \(C_f\) a une asymptote horizontale dont l’équation est \(y=l\).
\(\:\) - Si la limite n’existe pas, \(C_f\) n’a pas d’asymptote.
\(\:\)
Exemple : Si \(f(x)=x sin(x)\), \(C_f\) n’a pas d’asymptote car \(f(x)\) change constamment de signe quand \(x\) tend vers \(±\infty\).
Quand \(x\) tend vers une « valeur interdite » \(x_0\), la courbe peut avoir une asymptote verticale d’équation \(x=x_0\), mais ce n’est pas toujours le cas.
Exemple : Pour \(f(x)=x ln(x)\), \(C_f\) n’a pas d’asymptote en \(0\) car \(\lim \limits_{x \to x_0^+}f(x)=0\).
FAQ : tout savoir sur les asymptotes en mathématiques
Une asymptote peut-elle être « franchie » par la courbe ?
Oui. Une courbe peut couper une asymptote un nombre fini de fois : ce qui compte, c’est le comportement « au voisinage » (à l’infini ou près d’une valeur), pas l’absence d’intersection.
Quelle différence entre asymptote et tangente ?
Une tangente décrit le comportement de la courbe près d’un point précis, tandis qu’une asymptote décrit le comportement de la courbe « loin » (quand x tend vers l’infini) ou près d’une valeur où la fonction se comporte de façon extrême.
Est-ce qu’une fonction peut avoir plusieurs asymptotes horizontales ?
Oui. Il est possible d’avoir une asymptote horizontale différente à gauche et à droite : une quand x tend vers −∞ et une autre quand x tend vers +∞.
Pourquoi voit-on parfois une « asymptote » sur un graphique alors qu’elle n’existe pas ?
Certains tracés donnent l’illusion d’une droite limite (à cause de l’échelle, d’un zoom ou d’un domaine d’étude trop petit). Pour conclure, il faut toujours vérifier avec un raisonnement (et pas seulement à l’œil).
Quelle est l’erreur la plus fréquente sur les asymptotes en contrôle ?
Confondre « valeur interdite » et asymptote verticale : le fait qu’une fonction ne soit pas définie en un point ne suffit pas, il faut aussi analyser le comportement de la courbe au voisinage de ce point.
À quoi servent les asymptotes pour étudier une fonction ?
Elles aident à prévoir la forme globale de la courbe, à repérer ses zones « importantes » et à rendre un tableau de variations ou un tracé beaucoup plus fiable, surtout quand on travaille avec des fonctions rationnelles.