Tu as déjà travaillé avec des angles exprimés en degrés, que ce soit en géométrie ou en physique. Mais en analyse, et en particulier en trigonométrie, on introduit une nouvelle unité de mesure : le radian. Cette unité est inséparable de l’outil central qu’est le cercle trigonométrique, un cercle de rayon 1 qui permet de définir les fonctions trigonométriques et d’unifier la lecture des angles.
Le cercle trigonométrique va non seulement te donner une vision géométrique des angles, mais aussi t’aider à résoudre des équations trigonométriques, à travailler avec des fonctions périodiques, ou encore à comprendre les oscillations en physique.
Définition du cercle trigonométrique
Le cercle trigonométrique est un cercle de centre O et de rayon 1, tracé dans un repère orthonormé.
- Son centre est à l’origine \(O(0,0)\)
- L’axe des abscisses est pris comme axe de départ des angles.
- Les angles sont orientés : un angle est positif quand il correspond à une rotation dans le sens anti-horaire (sens direct), et négatif quand il correspond à une rotation dans le sens horaire.
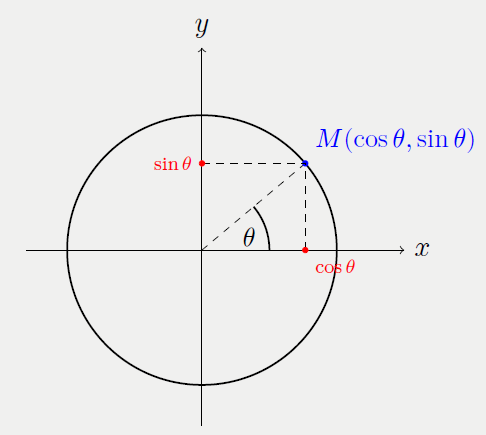
Chaque point \(M(x,y)\) du cercle est associé à un angle \(\theta\) mesuré à partir de l’axe des abscisses.
Les radians : une nouvelle unité
Traditionnellement, on mesure les angles en degrés. Mais en analyse, l’unité naturelle est le radian.
Par définition, un angle de 1 radian est celui qui intercepte sur le cercle un arc de longueur égale au rayon. Comme le cercle trigonométrique a pour rayon 1, cela veut dire que la mesure en radians correspond directement à la longueur de l’arc intercepté.
La circonférence du cercle étant \(2\pi\) tu en déduis que :
- Un tour complet correspond à \(2\pi\) radians.
- Un demi-tour correspond à \(\pi\) radians.
- Un quart de tour correspond à \(\frac{\pi}{2}\) radians.
Ainsi :
\(180° = \pi\) radians, \(360° = 2\pi\) radians
Cette correspondance facilite les calculs, car la trigonométrie en radians se simplifie grandement dans les formules.
Sinus et cosinus sur le cercle
Plaçons un point \(M\) sur le cercle trigonométrique correspondant à un angle \(\theta\). Ses coordonnées sont données par :
\(M(cos \theta , sin \theta)\)
C’est une définition fondamentale :
- L’abscisse du point correspond au cosinus de l’angle.
- L’ordonnée correspond au sinus de l’angle.
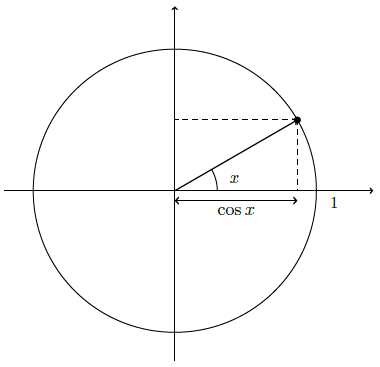
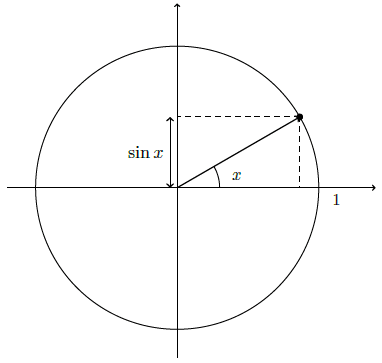
Cette association permet de visualiser immédiatement les valeurs du sinus et du cosinus à partir de la position d’un point sur le cercle.
De plus, comme le cercle est de rayon 1, la relation de Pythagore se traduit directement par :
\( \cos^2\theta + \sin^2\theta = 1\)
Angles remarquables
Certains angles reviennent très souvent en trigonométrie. Il est important de connaître leurs mesures en radians et les valeurs de sinus et cosinus associées.
| Angle en degrés | Angle en radians | \(\cos\theta\) | \(\sin\theta\) |
| \(0°\) | \(0\) | \(1\) | \(0\) |
| \(30°\) | \(\frac{\pi}{6}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) |
| \(45°\) | \(\frac{\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) |
| \(60°\) | \(\frac{\pi}{3}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) |
| \(60°\) | \(\frac{\pi}{2}\) | \(0\) | \(1\) |
| \(180°\) | \(\pi\) | \(-1\) | \(0\) |
| \(270°\) | \(\frac{3\pi}{2}\) | \(0\) | \(-1\) |
| \(360°\) | \(2\pi\) | \(1\) | \(0\) |
Apprendre ces valeurs par cœur te permettra de gagner beaucoup de temps dans les calculs.
Périodicité et symétries
L’un des grands avantages du cercle trigonométrique est de montrer la nature périodique des fonctions sinus et cosinus.
En effet :
\(\cos (\theta + 2\pi ) = \cos \theta\), \(\sin (\theta + 2\pi ) = \sin \theta\)
Cela signifie que les courbes de sinus et cosinus se répètent tous les \(2\pi\).
De plus, le cercle met en évidence certaines symétries :
- La fonction cosinus est paire : \(\cos (-\theta) = \cos \theta \)
- La fonction sinus est impaire : \(\sin (-\theta) = – \sin \theta \)
Ces propriétés sont directement visibles grâce au positionnement des points symétriques par rapport aux axes du cercle.
Applications du cercle trigonométrique
Le cercle trigonométrique n’est pas qu’une figure de cours abstraite. Il sert concrètement dans plusieurs domaines :
- En mathématiques pures, il donne accès à la résolution d’équations trigonométriques.
- En physique, il permet de modéliser les oscillations (comme le mouvement d’un pendule) et les phénomènes périodiques (ondes, courants alternatifs…).
- En informatique graphique, les coordonnées
- (cosθ,sinθ)
- (cosθ,sinθ) servent à tracer des cercles ou des courbes paramétrées.
- En géométrie analytique, il est un outil puissant pour décrire des rotations ou transformations.
Exercices
Exercice 1 :
Calcule \(\cos \theta \) et \(\sin \theta \) pour \(\theta = \frac{2\pi}{3}\).
Exercice 2 :
Résous l’équation : \( \sin \theta = \frac{\sqrt{2}}{2} \) dans l’intervalle \([0 ; 2\pi]\)
Correction
Exercice 1 :
\(\frac{2\pi}{3}\) correspond à \(120°\). Sur le cercle, cet angle est dans le 2e quadrant : le cosinus est négatif, le sinus est positif.
\(\cos \frac{2\pi}{3} = \frac{-1}{2}\), \(\sin \frac{2\pi}{3} = \frac{\sqrt{3}}{2}\)
Exercice 2 :
On connaît la valeur : \(\sin \frac{\pi}{4} = \frac{\sqrt{2}}{2}\). Mais comme la fonction sinus est positive dans le 1er et le 2e quadrant, il existe deux solutions :
\(\theta = \frac{\pi}{4}\) ou \(\theta = \frac{3\pi}{4}\)
Graphiquement, cela correspond aux points du cercle trigonométrique ayant la même ordonnée \(\frac{\sqrt{2}}{2}\).
Le cercle trigonométrique est bien plus qu’un simple cercle : il est la clé qui te permet de relier les angles aux valeurs des fonctions sinus et cosinus. Grâce à lui, tu visualises immédiatement la périodicité des fonctions trigonométriques, tu accèdes à la symétrie entre les quadrants, et tu bénéficies d’un véritable outil de résolution des équations trigonométriques.










