Imagine-toi face à un pendule de Galilée, balançant avec une régularité hypnotique. Dans l’idéal théorique, ce mouvement devrait se poursuivre éternellement, suivant les lois parfaites de la mécanique newtonienne. Pourtant, dans la réalité, chaque oscillation s’amenuise, l’amplitude décroît, et le pendule finit par s’immobiliser. Cette différence entre le modèle idéal et le comportement réel constitue l’essence même de l’étude des oscillateurs mécaniques amortis.
En physique, un oscillateur mécanique amorti est un système qui oscille tout en perdant progressivement de l’énergie à cause des frottements. Contrairement à l’oscillateur harmonique idéal, son amplitude diminue avec le temps jusqu’à l’arrêt. Dans cet article, tu vas comprendre ce qu’est un oscillateur amorti, comment on le modélise, quels sont les différents régimes d’amortissement (pseudo-périodique, critique, apériodique) et à quoi ils servent concrètement en ingénierie et en technologie.
Oscillateur harmonique et oscillateur amorti : du modèle idéal à la réalité
Oscillateur harmonique simple : modèle idéal sans amortissement
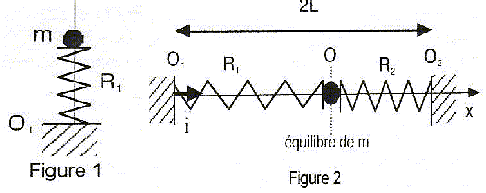
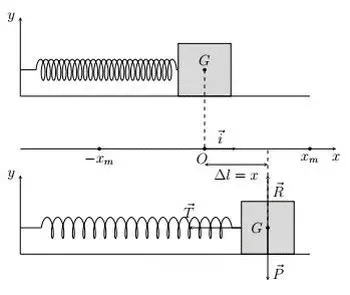
Un oscillateur harmonique idéal constitue l’archétype du mouvement périodique. Qu’il s’agisse d’un ressort de constante de raideur k supportant une masse m, ou d’un pendule simple de longueur l dans le champ gravitationnel terrestre, le comportement idéal obéit à l’équation différentielle fondamentale :
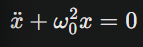
où ω0 représente la fréquence propre du système. Pour un oscillateur harmonique constitué d’un ressort, cette fréquence est donnée par:
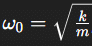
avec k la constante de raideur du ressort et m la masse attachée. Dans le cas d’un pendule simple, dans l’approximation des petites oscillations, la fréquence propre est exprimée par

Cette équation admet pour solution générale :
x(t)=Acos(ω0t+ϕ)
L’oscillateur idéal se distingue par sa période propre :
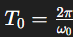
Celle-ci est indépendante de l’amplitude des oscillations. Cette caractéristique résulte du comportement harmonique du système, où la période de oscillation reste constante quel que soit l’écart initial de la position de départ. De plus, dans un oscillateur idéal, l’énergie mécanique totale du système est conservée tout au long du mouvement, cette énergie étant la somme de l’énergie cinétique et de l’énergie potentielle, et demeurant constante en l’absence de forces dissipatives.
.
Pourquoi l’amortissement est indispensable dans les oscillateurs réels ?
Dans la réalité physique, aucun oscillateur ne peut maintenir indéfiniment son mouvement. Les frottements, qu’ils soient dus à la résistance de l’air, aux frottements internes des matériaux, ou aux imperfections mécaniques, introduisent une dissipation énergétique continue. Cette réalité impose de réviser notre modélisation pour intégrer les phénomènes d’amortissement.
Modélisation de l’amortissement dans un oscillateur mécanique
Les différents types d’amortissement (visqueux, sec, quadratique)
L’amortissement se manifeste sous différentes formes selon la nature des forces dissipatives :
L’amortissement visqueux est dû à une force de frottement qui est proportionnelle à la vitesse du mouvement, et qui est caractéristique des systèmes en mouvement à travers un fluide visqueux. Cette force de frottement est modélisée par l’expression vectorielle suivante :

où γ désigne le coefficient de frottement visqueux, et v la vitesse du corps en mouvement. Ce phénomène est responsable de la dissipation d’énergie mécanique, entraînant une diminution progressive de l’amplitude des oscillations au fil du temps.
L’amortissement sec ou de Coulomb implique une force constante en module, mais opposée au mouvement, caractéristique du frottement solide.
L’amortissement quadratique fait intervenir une force proportionnelle au carré de la vitesse, prépondérante à haute vitesse dans un fluide turbulent.
Équation différentielle de l’oscillateur mécanique amorti
Lorsqu’on considère un amortissement visqueux, l’équation du mouvement pour un oscillateur devient :
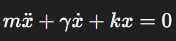
En divisant cette équation par la masse m et en posant :

on obtient l’équation canonique suivante :
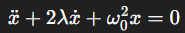
Le paramètre λ caractérise l’intensité de l’amortissement, qui dépend du coefficient de frottement visqueux et de la masse du système. Le facteur de qualité Q=ω0/2λ, quant à lui, mesure le rapport entre l’énergie stockée dans le système et l’énergie dissipée par cycle d’oscillation. Un facteur de qualité élevé correspond à un faible amortissement, tandis qu’un facteur de qualité faible indique un amortissement plus important, ce qui mène à une dissipation d’énergie plus rapide.
Régimes d’un oscillateur amorti selon le facteur de qualité Q
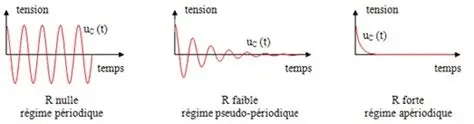
La nature des solutions de l’équation différentielle dépend étroitement de la valeur du discriminant, ce qui conduit à trois régimes distincts.
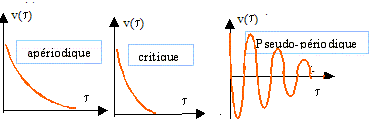
Régime critique : retour rapide à l’équilibre sans oscillation
Lorsque λ < ω0 (amortissement faible), le système oscille avec une amplitude décroissante exponentiellement. La solution s’écrit :
x(t)=A0e−λtcos(ωdt+ϕ)
où
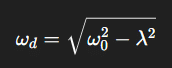
représente la pseudo-pulsation, légèrement inférieure à la pulsation propre. Ce régime, le plus fréquent dans les applications pratiques, conserve le caractère oscillatoire tout en manifestant une décroissance exponentielle de l’amplitude.
Régime critique : Q = 1/2
Le régime critique correspond à λ = ω0. Le système retourne à l’équilibre le plus rapidement possible sans dépasser sa position d’équilibre. La solution prend la forme :
x(t)=(A+Bt)e−λt
Ce régime présente un intérêt technologique majeur dans la conception d’amortisseurs optimisés.
Régime apériodique : amortissement fort sans oscillation
Pour un amortissement fort, le système n’oscille plus mais retourne lentement vers l’équilibre selon une décroissance purement exponentielle. Ce régime trouve des applications dans certains systèmes de stabilisation où l’on souhaite éviter tout dépassement.
Mesurer l’amortissement d’un oscillateur : méthode expérimentale
Protocole expérimental type
Une expérience caractéristique implique l’enregistrement des oscillations d’un pendule élastique ou d’un pendule simple en fonction du temps, idéalement avec des capteurs de position de haute précision. L’analyse des données permet d’extraire la pseudo-période, le coefficient d’amortissement, et de vérifier la validité du modèle théorique.

Applications des oscillateurs amortis en ingénierie et technologie
Oscillateurs amortis et amortisseurs automobiles
Les amortisseurs automobiles exploitent directement les principes de l’oscillateur amorti pour optimiser le confort et la sécurité. Le réglage du coefficient d’amortissement permet d’ajuster la réponse dynamique du véhicule selon les conditions d’usage.
Oscillateurs mécaniques amortis en horlogerie
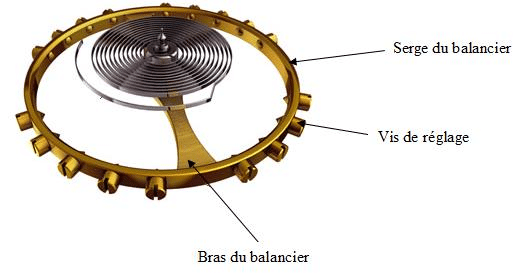
Les oscillateurs mécaniques constituent le cœur des montres mécaniques, où la maîtrise de l’amortissement conditionne la précision chronométrique. Le balancier-spiral fonctionne comme un oscillateur harmonique dont l’amortissement doit être minimisé pour maintenir la régularité.
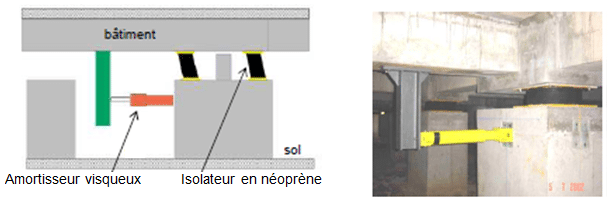
Oscillateurs amortis et génie parasismique
Dans les structures du génie civil, l’introduction contrôlée d’amortissement par des dispositifs spécialisés permet d’atténuer les oscillations induites par les séismes, protégeant ainsi l’intégrité des bâtiments.
Quiz sur les oscillateurs mécaniques amortis
- Quelle est la différence fondamentale entre un oscillateur idéal et un oscillateur réel ?
- Comment le facteur de qualité Q influence-t-il le comportement dynamique d’un oscillateur amorti ?
- Dans quel régime un oscillateur amorti présente-t-il encore des oscillations ?
- Explique le principe du décrément logarithmique pour mesurer l’amortissement.
- Cite trois applications technologiques où la maîtrise de l’amortissement est critique.
Réponses :
- Un oscillateur idéal conserve son énergie et oscille indéfiniment, tandis qu’un oscillateur réel perd de l’énergie par dissipation.
- Q détermine le régime : pseudo-périodique (Q > 1/2), critique (Q = 1/2), ou apériodique (Q < 1/2).
- Régime pseudo-périodique, quand l’amortissement est faible (Q > 1/2).
- Il mesure le rapport d’amplitudes successives pour calculer le coefficient d’amortissement.
- Amortisseurs automobiles, montres mécaniques, structures antisismiques.
Conclusion
L’étude des oscillateurs mécaniques amortis révèle la richesse d’un phénomène physique apparemment simple mais aux implications considérables. Du ressort de laboratoire aux structures architecturales, de l’horlogerie de précision aux systèmes de contrôle industriel, la compréhension de l’amortissement constitue une clé fondamentale de l’ingénierie moderne.
Cette exploration théorique et expérimentale des oscillateurs réels illustre parfaitement comment la physique fondamentale nourrit l’innovation technologique. La maîtrise de ces concepts te permet non seulement de comprendre les phénomènes naturels, mais aussi de participer à la conception des systèmes techniques de demain.
Comprendre les oscillateurs mécaniques amortis, leurs régimes et leurs applications, c’est maîtriser un concept central de la physique du mouvement et de l’ingénierie moderne.