Le courant continu est au cœur de la plupart des objets électroniques que tu utilises au quotidien, du smartphone à l’ordinateur portable. Derrière ces technologies se cachent pourtant des principes simples : une tension, un courant qui circule dans un seul sens et quelques composants essentiels. Comprendre le fonctionnement des circuits en courant continu, la loi d’Ohm et les montages de base permet non seulement de réussir ses exercices de physique, mais aussi de mieux saisir comment l’électricité alimente le monde moderne.
Comprendre le courant continu
Le courant électrique est un phénomène que tu utilises tous les jours, sans forcément y penser. Ton téléphone, ton ordinateur portable ou encore les petites lampes LED fonctionnent généralement grâce à du courant continu (DC pour Direct Current), fourni par une batterie ou une pile. Mais qu’est-ce que cela signifie ?
Dans un circuit électrique, les charges (électrons) se déplacent grâce à une différence de potentiel, c’est-à-dire une tension appliquée entre deux points. Lorsque le courant circule toujours dans le même sens, on parle de courant continu. C’est ce qui distingue ce type de courant du courant alternatif (AC), celui qui alimente les prises électriques de ta maison, où la direction du courant change périodiquement.
Sans courant continu, impossible d’alimenter les circuits électroniques modernes ! Les ingénieurs l’utilisent dans l’électronique, l’automobile électrique, mais aussi dans des infrastructures gigantesques, comme certaines lignes de transport d’électricité en haute tension.
Les composants essentiels
Pour comprendre les circuits en courant continu, il faut d’abord connaître leurs éléments constitutifs. Un circuit n’est rien d’autre qu’un chemin fermé où circule le courant. On y trouve généralement :
- Un générateur (batterie ou pile) : il fournit la tension, c’est-à-dire « l’énergie » qui pousse les électrons à circuler.
- Un conducteur (souvent un fil métallique) : il sert de réseau de circulation.
- Un récepteur (lampe, moteur, résistance…) : il consomme l’énergie électrique pour produire un effet utile (lumière, chaleur, mouvement).
- Une résistance (ou résistor) : son rôle est d’opposer une certaine résistance au passage du courant. Elle sert notamment à protéger les composants.
Ces éléments sont représentés dans un schéma électrique, un langage universel qui permet aux scientifiques et ingénieurs de comprendre instantanément le fonctionnement du circuit.
Langage des schémas électriques
En sciences, le schéma vaut mieux qu’un long discours. Les circuits électriques utilisent des symboles normalisés que tu devrais mémoriser si tu veux progresser en physique. Parmi les plus importants :
- Pile ou générateur : deux traits parallèles, l’un long (borne +), l’autre court (borne –).
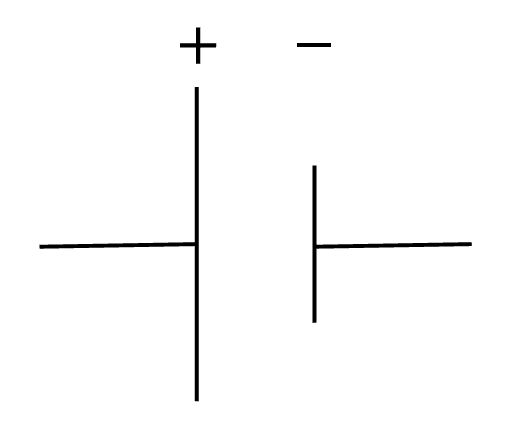
- Résistance : un simple rectangle.

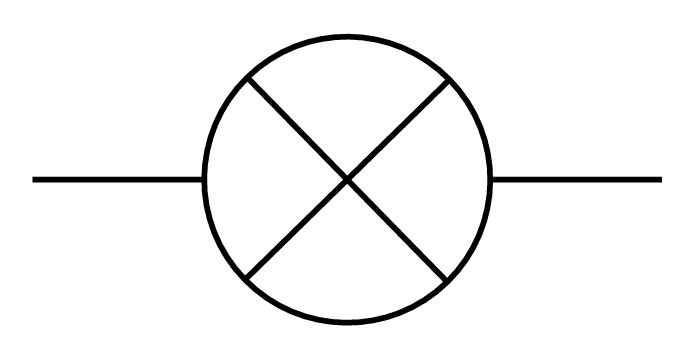
- Lampe : un rond avec une croix à l’intérieur.
- Interrupteur : une coupure dans la ligne, parfois fermée (circuit passant), parfois ouverte (coupé).
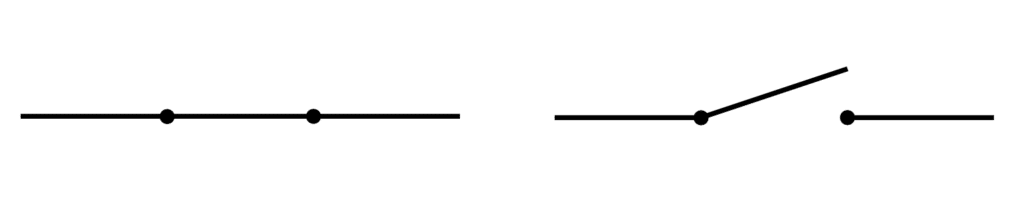
La loi d’Ohm
Place maintenant à un pilier fondamental de l’électricité : la loi d’Ohm. Sans exagération, on peut dire qu’elle est à l’électricité ce que les équations de Newton sont à la mécanique.
Formulée par le physicien allemand Georg Simon Ohm au XIXe siècle, elle établit que la tension (\( U \)) appliquée à une résistance est proportionnelle à l’intensité (\( I \)) qui la traverse, avec pour facteur constant la résistance (\( R \)) :
\( U = R\times I \)
- \( U \) (tension) se mesure en volts (\( V \)).
- \( I \) (intensité) se mesure en ampères (\( A \)).
- \( R \) (résistance) se mesure en ohms (\( \Omega \)).
C’est une relation très simple, mais universelle dès qu’un conducteur obéit aux lois de l’électricité classique. Grâce à elle, nous pouvons dimensionner un circuit et éviter qu’il ne soit détruit par une trop forte intensité.
Énergie et puissance électrique
Le courant ne circule pas pour rien : on attend de lui qu’il produise une lumière, un mouvement ou encore de la chaleur. Cet effet est mesuré par la puissance électrique (P) :
\( P = U \times I \)
Une ampoule de \( 12 V \) parcourue par un courant de \( 0,5 A \) consomme par exemple :
\( P = 12 \times 0,5 = 6 W \)
Cette notion relie directement les lois de l’électricité à l’usage concret de l’énergie. Tu peux d’ailleurs établir une relation directe avec la résistance :
\( P = R \times I^2 = \frac{U^2}{R} \)
Ces formules sont essentielles pour comprendre pourquoi certains appareils consomment beaucoup plus d’énergie que d’autres, et pourquoi les ingénieurs cherchent sans cesse à concevoir des circuits plus efficaces.
Séries et dérivations
Un circuit n’est pas forcément composé d’un seul composant : tu peux en associer plusieurs. Deux cas classiques existent :
- Montage en série : les composants sont alignés les uns à la suite des autres. Ils partagent la même intensité, mais la tension totale se divise entre eux. Exemple : des petites lampes de guirlande en série.

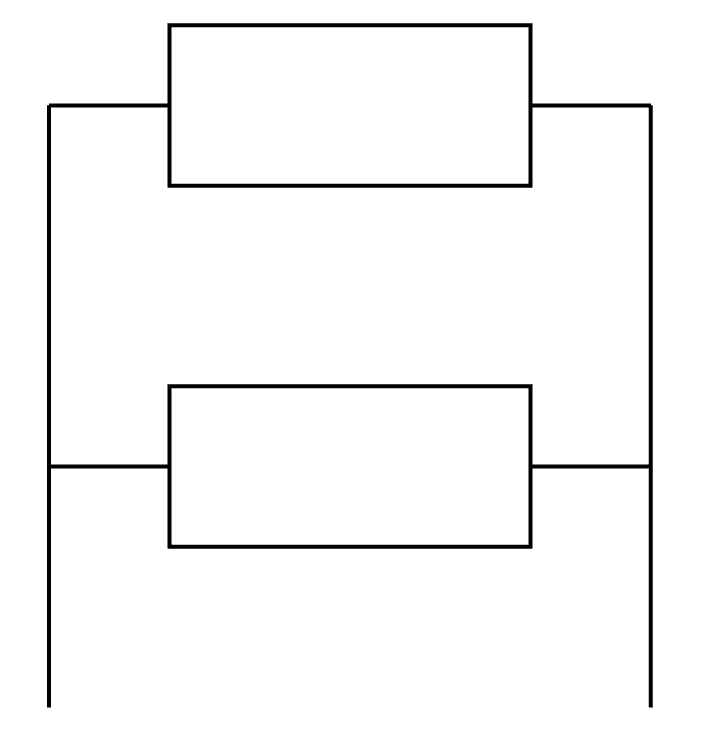
- Montage en dérivation (ou parallèle) : chaque composant est relié directement aux bornes du générateur. Ils partagent la même tension, mais l’intensité totale est répartie. Exemple : les ampoules de la maison branchées sur une même ligne électrique.
Exercices pratiques
Pour t’entraîner, voici trois exercices avec leur correction. N’hésite pas à sortir papier et crayon pour les résoudre avant de regarder la solution.
Exercice 1
Une lampe de résistance \( 6 \Omega \) est branchée sur une pile de \( 12 V \). Calcule l’intensité qui traverse la lampe.
Correction
En appliquant la loi d’Ohm :
\( I = \frac{U}{R} = \frac{12}{6} = 2 A \)
L’intensité est de 2 ampères.
Exercice 2
On associe deux résistances en série : \( 4 \Omega \) et \( 8 \Omega \), reliées à une pile de \( 24 V \). Quelle est l’intensité dans le circuit ? Quelle est la tension aux bornes de chaque résistance ?
Correction
Résistance équivalente en série :
\( R_{eq} = 4 + 8 = 12 \Omega \)
Intensité :
\( I = \frac{U}{R_{eq}} = \frac{24}{12} = 2 A \)
Tension sur chaque résistance :
- Pour \( 4 \Omega \) : \( U = R \times I = 4 \times 2 = 8 V \)
- Pour \( 8 \Omega \) : \( U = R \times I = 8 \times 2 = 16 V \)
Exercice 3
Un circuit comporte deux résistances en parallèle : \( 10 \Omega \) et \( 20 \Omega \), branchées sur une pile de \( 30 V \). Calcule l’intensité totale fournie par la pile.
Correction
En dérivation, la tension est la même sur chaque branche, soit \( U = 30 V \).
- Intensité dans la première résistance : \( I_1 = \frac{U}{R} = \frac{30}{10} = 3 A \)
- Intensité dans la seconde résistance : \( I_2 = \frac{U}{R} = \frac{30}{20} = 1,5 A \)
Intensité totale :
\( I = I_1 + I_2 = 3 + 1,5 = 4,5 A \)
Tu vois à quel point la compréhension d’un circuit électrique repose d’abord sur quelques lois très accessibles. Grâce à la loi d’Ohm, aux montages en série et en parallèle, tu peux déjà résoudre des problèmes pratiques et anticiper le comportement d’un circuit. Ces bases sont indispensables avant d’aller explorer l’électronique plus avancée, comme les condensateurs ou les bobines.
La physique de l’électricité est un formidable terrain de jeu : chaque formule que tu apprends te permet d’expliquer un objet de ton quotidien. La prochaine fois que tu brancheras ton téléphone pour le recharger, souviens-toi que ce geste s’explique… grâce à la loi d’Ohm !